快速响应矩阵码(下)
书接上回,继续下半场。
纠错码
QR 码采用纠错算法生成一系列纠错码字,添加在数据码字序列之后,使得符号可以在遇到损坏时可以恢复。这就是为什么二维码即使有残缺也可以扫出来。没有残缺创造残缺也要把它扫出来,相信大家见过很多中间带图标的二维码吧。
纠错码字可以纠正两种类型的错误,拒读错误(错误码字的位置已知)和替代错误(错误码字位置未知)。一个拒读错误是一个没扫描到或无法译码的符号字符,一个替代错误是错误译码的符号字符。如果一个缺陷使深色模块变成浅色模块,或将浅色模块变成深色模块,将符号字符错误地译码为是另一个不同的码字,造成替代错误,这种数据替代错误需要两个纠错码字来纠正。
纠错等级
纠错共有 4 个等级,对应 4 种纠错容量,如下表所示。
| 纠错等级 | L | M | Q | H |
|---|---|---|---|---|
| 纠错容量,%(近似值) | 7 | 15 | 25 | 30 |
用户应确定合适的纠错等级来满足应用需求。从 L 到 H 四个不同等级所提供的检测和纠错的容量逐渐增加,其代价是对表示给定长度数据的符号的尺寸逐渐增加。例如,一个版本为 20-Q 的符号能包含 485 个数据码字,如果可以接受一个较低的纠错等级,则同样的数据也可用版本 15-L 的符号表示(准确数据容量为 523 个码字)。
纠错等级的选择与下列因素相关:
- 预计的符号质量水平:预计的符号质量等级越低,应用的纠错等级就应越高。
- 首读率的重要性。
- 在扫描误读失败后,再次扫描的机会。
- 印刷符号的空间限制了使用较高的纠错等级。
纠错等级【L】适用于具有高质量的符号以及/或者要求使表示给定数据的符号尽可能最小的情况。等级【M】被认为是“标准”等级,它具有较小尺寸和较高的可靠性。等级【Q】是具有“高可靠性”的等级,适用于一些重要的或符号印刷质量差的场合,等级【H】提供可实现的最高的可靠性。
纠错码字的生成
QR 码的纠错使用 Reed–Solomon 编码,有关 Reed–Solomon 码,可以参考这篇文章:http://article.iotxfd.cn/RFID/Reed%20Solomon%20Codes。这里我只大概介绍一下计算过程。
纠错码字的生成多项式
纠错码字是用数据码字除纠错码多项式所得到的余数。纠错码多项式我们可以查表得出,首先查下表 3:QR码符号各版本的纠错特性。这里我仅列出小部分,完整表数据请查看 GB/T 18284-2000 中的表 9。
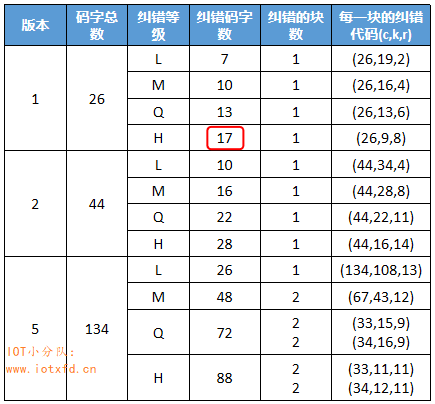
其中(c,k,r):c=码字总数;k=数据码字数;r=纠错容量。
之前【例 1 续 1】确定使用的是版本1-H,查表得到纠错码字数为:17(上表红框部分)。码字总数为 26 表示此版本 QR 码可容纳的总数据量,其中数据码字占 9 个,纠错码字占 17 个。接下来根据纠错码字数 17 来查找多项式。可在 GB/T 18284-2000 附录 A 的纠错码字的生成多项式表中查找,也可使用生成多项式工具创建它,下表 4 只列出小部分内容:

Reed–Solomon 码的 C# 实现
大家可能会问了,之前生成的纠错码字怎么跟这个多项式除啊?直接除肯定是不行的,首先要把查到的多项式转化为对应的一组数字。上表查到 17 所对应的生成多项式可转化为:[1, 119, 66, 83, 120, 119, 22, 197, 83, 249, 41, 143, 134, 85, 53, 125, 99, 79]。用数据码字除这组数字所得余数,就是我们的纠错码字了。当然,这个过程是使用程序来完成的。Reed–Solomon 编码这篇文章详细讲述了如何使用 Python 实现这个功能。我将需要用到的代码翻译成了 C#:
using System;
namespace QRHelper
{
class ECC
{
const int PRIM = 0x11d;
private static byte[] gfExp = new byte[512]; //逆对数(指数)表
private static byte[] gfLog = new byte[256]; //对数表
static ECC()
{
byte x = 1;
for (int i = 0; i <= 255; i++)
{
gfExp[i] = x;
gfLog[x] = (byte)i;
x = Gf_MultNoLUT(x, 2);
}
for (int i = 255; i < 512; i++)
{
gfExp[i] = gfExp[i - 255];
}
}
//伽罗华域乘法
private static byte Gf_MultNoLUT(int x, int y)
{
int r = 0;
while (y != 0)
{
if ((y & 1) != 0)
{
r ^= x;
}
y >>= 1;
x <<= 1;
if ((x & 256) != 0)
{
x ^= PRIM;
}
}
return (byte)r;
}
//伽罗华域乘法
private static byte GfMul(byte x, byte y)
{
if (x == 0 || y == 0)
{
return 0;
}
return gfExp[gfLog[x] + gfLog[y]];
}
//伽罗华域幂
private static byte GfPow(byte x, int power)
{
return gfExp[(gfLog[x] * power) % 255];
}
//多项式 乘法
private static byte[] GfPolyMul(byte[] p, byte[] q)
{
byte[] r = new byte[p.Length + q.Length - 1];
for (int j = 0; j < q.Length; j++)
{
for (int i = 0; i < p.Length; i++)
{
r[i + j] ^= GfMul(p[i], q[j]);
}
}
return r;
}
/// <summary>
/// 获取纠错码字的生成多项式
/// </summary>
/// <param name="nsym">纠错码字数</param>
/// <returns>由一组数字表示的生成多项式</returns>
public static byte[] RsGeneratorPoly(int nsym)
{
byte[] g = { 1 };
for (int i = 0; i < nsym; i++)
{
g = GfPolyMul(g, new byte[] { 1, GfPow(2, i) });
}
return g;
}
/// <summary>
/// 生成纠错码,并添加在数据码字之后
/// </summary>
/// <param name="msgIn">数据码字</param>
/// <param name="nsym">纠错码字数</param>
/// <returns>数据码字+纠错码字</returns>
public static byte[] RsEncodeMsg(byte[] msgIn, int nsym)
{
if (msgIn.Length + nsym > 255)
{
throw new ArgumentException("数组长度超过 255!");
}
//byte[] gen = generators[(byte)nsym];
byte[] gen = RsGeneratorPoly(nsym);
byte[] msgOut = new byte[msgIn.Length + gen.Length - 1];
Array.Copy(msgIn, 0, msgOut, 0, msgIn.Length);
for (int i = 0; i < msgIn.Length; i++)
{
byte coef = msgOut[i];
if (coef != 0)
{
for (int j = 1; j < gen.Length; j++)
{
msgOut[i + j] ^= GfMul(gen[j], coef);
}
}
}
Array.Copy(msgIn, 0, msgOut, 0, msgIn.Length);
return msgOut;
}
}
}
代码量是相当少啊!根据不用上网找算法包。在实际开发中,如果需要绘制大量 QR 码,完全可以将所有 31 个生成多项式转化结果存放在集合中,使用时直接查询即可得出,这样可以大大加快生成速度。上述代码中的RsGeneratorPoly()方法用于生成多项式,它会产生大量临时数组。有了代码,可以继续我们之前的例子了。
【例 1 续 2】:生成完整码字
之前在【例 1 续 1】中,我们已经生成了数据码字:
00010000,00100000,00001100,01010110,01100001,10000000,11101100,00010001,11101100
16 进制表示形式为:0x10, 0x20, 0x0C, 0x56, 0x61, 0x80, 0xEC, 0x11, 0xEC
接下来使用如下代码生成完整码字:
byte[] msgin = { 0x10, 0x20, 0x0C, 0x56, 0x61, 0x80, 0xEC, 0x11, 0xEC };
byte[] msg = ECC.RsEncodeMsg(msgin, 17);
得到结果:0x10 0x20 0x0C 0x56 0x61 0x80 0xEC 0x11 0xEC 0x0E 0x9D 0x02 0xC8 0xC2 0x94 0xF3 0xA7 0xAD 0x8D 0xE2 0x0A 0xF4 0xA5 0x2B 0xAC 0xDF
以上就是我们要填入 QR 码图案的所有 26 个码字了。前 9 个为数据码字,后 17 个为纠错码字,程序已经帮我们自动连接好了。
构造信息的最终码字序列
上例中,纠错的块数只有 1 块,只需简单将数据码字连接纠错码字连接,组成 1 块数据即可。而在绝大多数版本中,存在多个纠错码块数。下面讲解多块纠错码块折构造。
以版本 5-H 举例,查表 3 的版本 5 部分,如下所示:
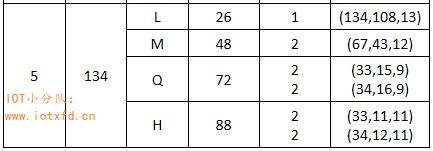
版本 5-H 码字共分为 4 块,其中 2 块码字总数为 33 个,包括 11 个数据码字和 22 个纠错码字;另 2 块码字总数为 34 个,包括 12 个数据码字和 22 个纠错码字。首先取出数据码字的前 11 个数据码字,计算 22 个纠错码字,连接形成块 1 数据;再从数据码字中取 11 个码字生成块 2 数据;继续从数据码字中取 12 个码字生成块 3 数据;将最后 12 个数据码字取出并生成块 4 数据。
各块字符的按下表进行布置,表中的每一行对应一个块的数据码字(表示为Dn)和相应块的纠错码字(表示为En);

版本 5-H 符号的最终码字序列为:
D1,D12,D23,D35,D2,D13,D24,D36,...D11,D22,D33,D45,D34,D46,E1,E23,E45,E67,E2,E24,E46,E68,...E22,E44,E66,E88。在某些版本中,需要 3、4 或 7 个剩余位方能填满编码区域模块数,此时需在最后的码字后面加上剩余位(0)。
格式信息
格式信息用于存放纠错等级和掩模信息,是一个 15 数据,由 2位纠错指示符 + 3位掩模图形参考 + 10位纠错码组成。
格式信息的计算
首先纠错指示符由 2 个位表示,各纠错等级所对应的数字见下表5。
| 纠错等级 | L | M | Q | H |
|---|---|---|---|---|
| 二进制指示符 | 01 | 00 | 11 | 10 |
掩模图形参考使用 3 个位表示,由数字 0~7 表示,将其转换为 3 位二进制即可,掩模将在稍后介绍,现在你只需要知道占用 3 个位就行了。
将 2位纠错指示符 + 3位掩模图形参考,得到 5 位数据码,并使用 BCH(15,5) 编码计算得到纠错码。
BCH 码
BCH 码和 Reed–Solomon 码类似,可以参考 Reed–Solomon 编码这篇文章。Reed–Solomon 码使用多项式除法得出纠错码序列,而 BCH 码就简单得多,它按位运算得出纠错码。BCH(15,5) 表示 BCH 码总长度为 15 位,其中数据码为 5 位,纠错码 10 位。Reed–Solomon 码有生成多项式,BCH 码使用的是生成码:10100110111。使用数据码除以生成码,所得余数就是纠错码。由于 BCH 码的运算很简单,下面演示数据码 00101 的演算过程。
- 将数据码左移 10 位,凑够 15 位,得到二进制数字:001010000000000
- 将上面数字除以 10100110111(0x537),使用长除法,如下图所示:
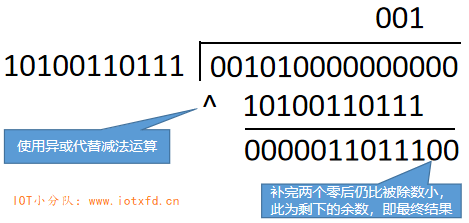
上图中的余数取 10 位即为纠错码:0011011100
- 将 5 位数据码 00101 与纠错码相连,即得到最终格式信息码:001010011011100(0x14DC)
使用程序实现非常简单,在ECC类中添加如下代码:
//生成 BCH 码
private static int CheckFormat(int fmt)
{
int g = 0x537;
for (int i = 4; i >= 0; i--)
{
if ((fmt & (1 << (i + 10))) != 0)
{
fmt ^= g << i;
}
}
return fmt;
}
/// <summary>
/// 生成 BCH(15,5) 纠错码,并返回完整格式信息码
/// </summary>
/// <param name="data">数据码</param>
/// <returns>返回完整格式信息码</returns>
public static int BCH_15_To_5_Encode(int data)
{
data <<= 10;
return data ^ CheckFormat(data);
}
使用以下代码生成完整格式信息码:
int code = ECC.BCH_15_To_5_Encode(5);
结果为:5340(0x14DC)
格式信息的掩模
为确保纠错等级和掩模图形参考(稍后介绍)合在一起的结果不全是 0,需将 15 位格式信息与掩模图形 101010000010010(0x5412)进行异或运算。
格式信息的绘制
QR 码中有专门的区域绘制格式信息,见下图:
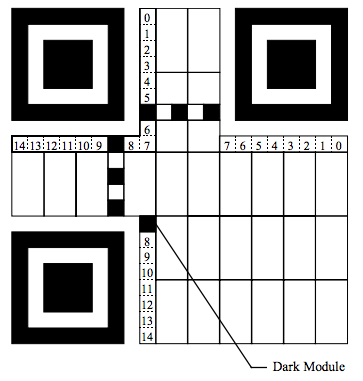
由于格式信息的正确译码对整个符号的译至关重要,它会在 QR 码中绘制两次以提供冗余。格式信息的最低位模块编号为 0,最高位编号为 14。为避免混淆,下表标示了之前生成格式信息与掩模图形以及两者进行 XOR 运算之后的结果的各个位编号。

左上角绘制区域编号 8、9 之间和 5、6 之间的深色模块被定位图形使用,不用于绘制格式信息。左下角编号 8 上的 Dark Module 永远为深色模块,不用于存放任何信息。
接下来我们将 XOR 后的结果绘制到 QR 码中的格式信息区域,如下图所示:

图中绿色区域为格式信息区域,其中浅绿色表示浅色模块,深绿色表示深色模块。
【例 1 续 3】:生成格式信息
接下来我继续【例 1】,添加格式信息:
- 之前【例 1】中我们选择了纠错等级为 H,查表 5,得到数字:10
- 假设我们选择的掩模图形参考为 011,则最终数据码为:10011
- 使用之前的程序将 10011 生成完整格式信息码:100110111000010(0x4DC2)
- 将生成的格式信息码与 101010000010010(0x5412)进行异或运算,结果为:
001100111010000(0x19D0) - 将结果绘制到格式信息区域中,最终结果如下图所示:
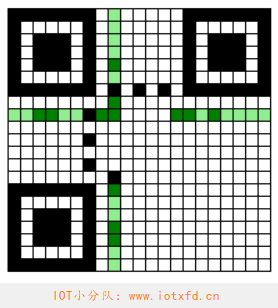
版本信息
版本信息用于存放 QR 码的版本号。其中,6 位数据位,12 位通过 BCH(18,6) 编码计算出的纠错位。只有版本 7~40 的符号包含版本信息。版本 0~6 无需绘制版本号。
版本信息的计算
版本信息的计算和格式信息类似,也是使用长除法。只是这一次使用的生成码为:1111100100101(0x1F25)。以下为 BCH(18,6) 的 C# 代码:
public static int BCH_18_6_Encode(int data)
{
int g = 0x1F25;
int fmt = data << 12;
for (int i = 5; i >= 0; i--)
{
if ((fmt & (1 << (i + 12))) != 0)
{
fmt ^= g << i;
}
}
return (data << 12) ^ fmt;
}
下面以版本号 7 为例,计算版本信息码:
- 版本号 7 转换为 6 位二进制数据码:000111
- 将以上数据码左移 12 位,凑够 18 位:000111000000000000
- 将上面数字除以生成码 1111100100101(0x1F25),得到余数:110010010100
- 将数据码与得到的余数相连,得到最终版本信息码:000111110010010100
与格式信息不同,版本信息码生成后不再需要单独进行掩模运算。
版本信息的绘制
由于版本信息的正确译码是整个符号正确译码的关键,因此版本信息在符号中出现两次以提供冗余。第一个存放位置在定位图形上面,由6行×3列模块组成,其右紧临右上角位置探测图形的分隔符;第二个存放位置在定位图形左侧,其下边紧临左下角位置探测图形的分隔符,如下图的蓝色部分所示:

格式信息的最低位模块编号为 0,最高位编号为 17。接下来我们将之前计算的版本 7 的版本信息码绘制到 QR 码中的版本信息区域。效果如下图所示,红色部分为版本信息,其中,深红色代表深色模块,粉红色代表浅色模块。:

至此,所有功能图形以及格式图形都已经绘制完毕,并已全部显示在这上图中。接下来,终于可以开始绘制数据码字了。
符号字符的布置
在 QR 码符号的编码区域中,符号字符以 2 个模块宽的纵列从符号右下角开始布置,并自右向左,且交替地从下向上或从上向下安排。GB/T 18284-2000 用了很长一段篇幅讲解编码布置规则,其实很简单,就是以两列为单位向上或向下布置,列内蛇形走位,遇障碍跳过。为方便大家学习,我在《QR助手程序》中加入了绘制走位路线的功能,下图是版本1和版本7的走位路线:
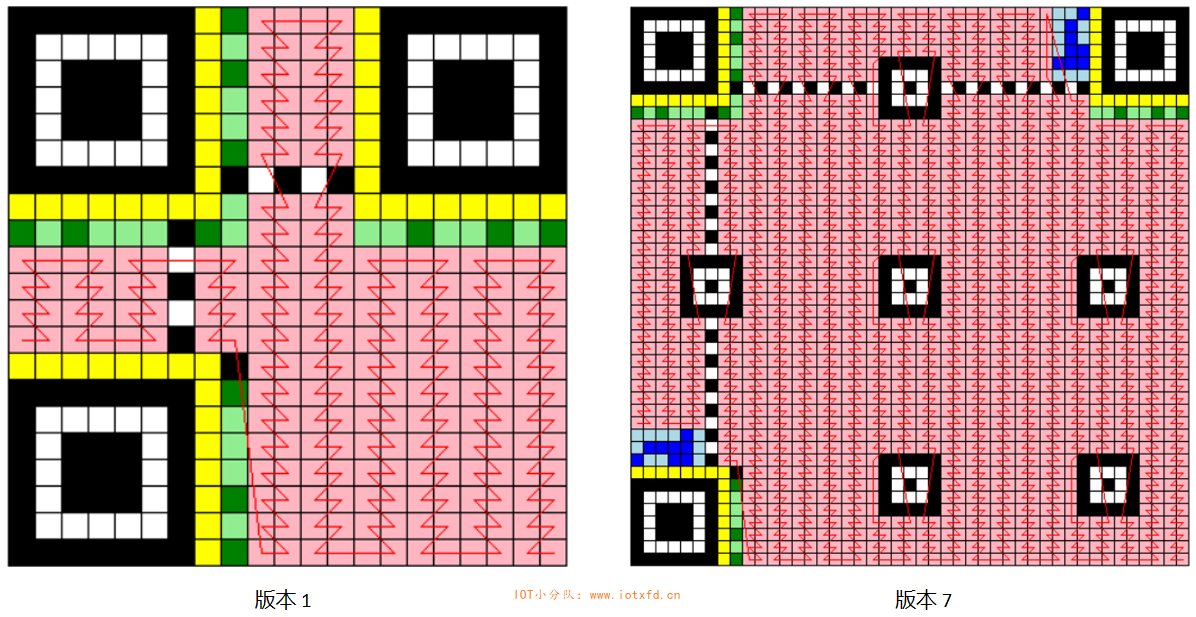
这飘忽不定的神仙步伐,销魂啊!从右下角开始,延着一条不中断的线一直到左下角结束,将最终数据码流从左到右,按这条线的方向布置在沿途遇到的粉红色模块中,即完成符号字符的布置。相信大家一眼就能看懂。我之所以要实现这个走位路线的绘制功能,一方面是手绘这两张图太痛苦了,另一方面也是为了方便验证走位算法是否存在错误。
【例 1 续 4】:布置符号字符
【例 1 续 2】中我们生成了最终的数据码字为:
0x10 0x20 0x0C 0x56 0x61 0x80 0xEC 0x11 0xEC 0x0E 0x9D 0x02 0xC8 0xC2 0x94 0xF3 0xA7 0xAD 0x8D 0xE2 0x0A 0xF4 0xA5 0x2B 0xAC 0xDF
现在终于可以将其依照之前的路线填入编码区域中了。效果如下图所示:
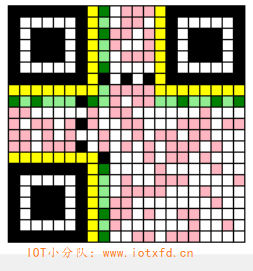
图中粉红色模块就是我们刚才填入的数据。终于可以庆祝一下了,放松一下可以,但不能端酒!事情还没完!
掩模
QR 码中如果出现大面积的空白或黑块,会导致扫描器识别困难。为了让 QR 图形看起来尽可能凌乱,且尽可能避免位置探测图形中的位图 1011101 的出现,需对 QR 图形进行掩模操作,步骤如下:
- 掩模不用于功能图形及格式图形:寻像图形、定位图形、校正图形、位置探测图形分隔符、格式信息和版本信息。
- 数据码字与掩模图形进行 XOR 操作后再进行绘制。
- 对每个结果图形的不合要求的部分记分,以评估这些结果。
- 选择得分最低的图形。
掩模图形
下表给出了掩模图形的参考和掩模图形生成的条件。掩模图形是通过将编码区域(不包括格式信息和版本信息)内那些条件为真的模块定义为深色而产生的。所示的条件中,i 代表模块的行的位置,j 代表模块的列的位置,(i,j)=(0,0)代表符号中左上角的位置。
| 掩模图形参考 | 条件 |
|---|---|
| 000 | (i + j) mod 2 = 0 |
| 001 | i mod 2 = 0 |
| 010 | j mod 3 = 0 |
| 011 | (i + j) mod 3 = 0 |
| 100 | ((i/2)+(j/3)) mod 2 = 0 |
| 101 | (i × j) mod 2 + (i × j) mod 3 = 0 |
| 110 | ((i × j) mod 2 + (i × j) mod 3) mod 2 = 0 |
| 111 | ((i × j) mod 3 + (i + j) mod 2) mod 2 = 0 |
下图显示了所有掩模图形的外观:
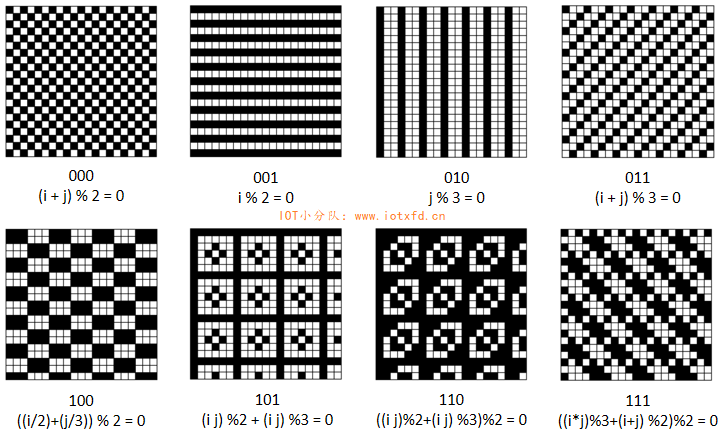
下面是掩模后的效果,我们可以看到整块的数据掩模后变得比较零散了。
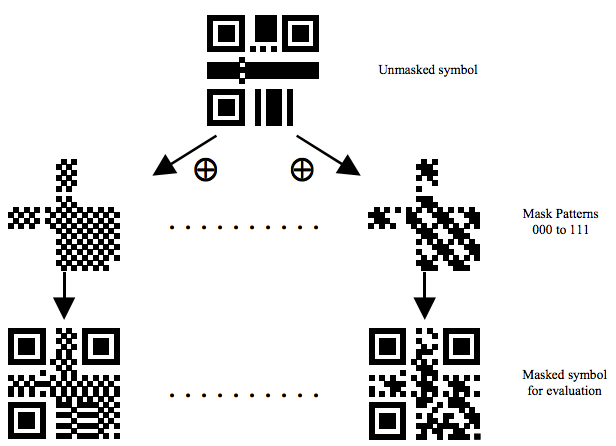
【例 1 续 5】:加入掩模图形
最后,我们将【例 1 续 4】得到的图案中的粉红色模块同掩模图案进行 XOR 运算。将所有深色图案用黑色替换,浅色图案用白色替换,得到最终的二维码。激动啊!终于完工!下图是使用所有 8 种掩模得到的结果,每个 QR 码都可以扫出 01234567。

到现在我才知道程序没有写错,在没写完文章之前,根本没办法测试,心里的一块石头终于落地了。要是最终图案扫码失败,真不知道上哪找错误去。文章终于写完,真不容易,学习、查资料、写作,还得 Coding。还好,文章总算变成成品了,不过程序还没写完。现在的程序只够写文章用,还要加好多东西。休息,慢慢来吧。