一、 图的定义
二、图的遍历
一、 图的定义
1.图是由顶点的有穷非空集和顶点之间边的集合,通常表示为:G(V. E),其中,G 表示一个图,V 是图 G 中顶点的集合,E 是图 G 中边的集合。
- 在线性表中,数据元素之间是被串起来的,仅有线性关系,每个数据元素只有一个直接前驱和一个直接后继。
- 在树形结构中,数据元素之间有着明显的层次关系,并且每一层上的数据元素可能和下一层中多个元素相关,但只能和上一层中一个元素相关。
- 图是一种较线性表和树更加复杂的数据结构,在图结构中,节点之间的关系可以是任意的,图中任意两个数据元素之间都可能相关。
线性表中我们把数据元素叫元素;树种将数据元素叫结点;在图中数据元素,我们称之为顶点。
线性表中可以没有数据元素,称为空表;树种可以没有结点,叫做空树;但在图结构中,不允许没有顶点。在定义中,若 V 是顶点的集合,则顶点集合 V 有穷非空。
线性表中,相邻的元素之间具有线性关系;树结构中,相邻两层的结点具有层次关系;而图中,任意两个顶点之间都可能有关系,顶点之间的逻辑关系用边来表示,边集可以是空的。
2 .各种图定义
-
无向边:若顶点 V1 到 V2 之间的边没有方向,则称这条边为无向边,用无序偶对来表示。如果途中任意两个顶点之间都是无向边,则称该图为无向图。如下图:
 无向图
无向图
由于是无方向的,连接顶点 A 与 D 的边,可以表示成无序对 (A,D),也可以表示成 (D,A)。
-
有向边:若顶点 V1 到 V2 的边有方向,则称这条边为有向边,也称为弧。用有序偶<Vi, Vj> 来表示,Vi 称为弧尾,Vj 称为弧头。如果图中任意两个顶点之间的边都是有向边,则称该图为有向图。如下图:
 有向图
有向图 -
连接顶点 A 到 D 的有向边就是弧,A 是弧尾,D 是弧头,<A, D> 表示弧,注意不能写成<D, A>。
在无向图中,如果任意两个顶点之间都存在边,则称该图为无向完全图。含有 n 个顶点的无向完全图有 n * (n - 1) / 2 条边。

在有向图中,如果任意两个顶点之间都存在方向互为相反的两条弧,则称该图为有向完全图。含有 n 个顶点的有向完全图有 n * (n - 1) 条边。

从这里可以得出结论,对于具有 n 个顶点和 e 条边数的图,无向图 0<= e <= n(n-1)/2,有向图 0 <= e <= n(n-1)。
二、图的遍历
从图中某一顶点出发访遍图中其余顶点,且使每一个顶点仅被访问一次,这一过程就叫做图的遍历。
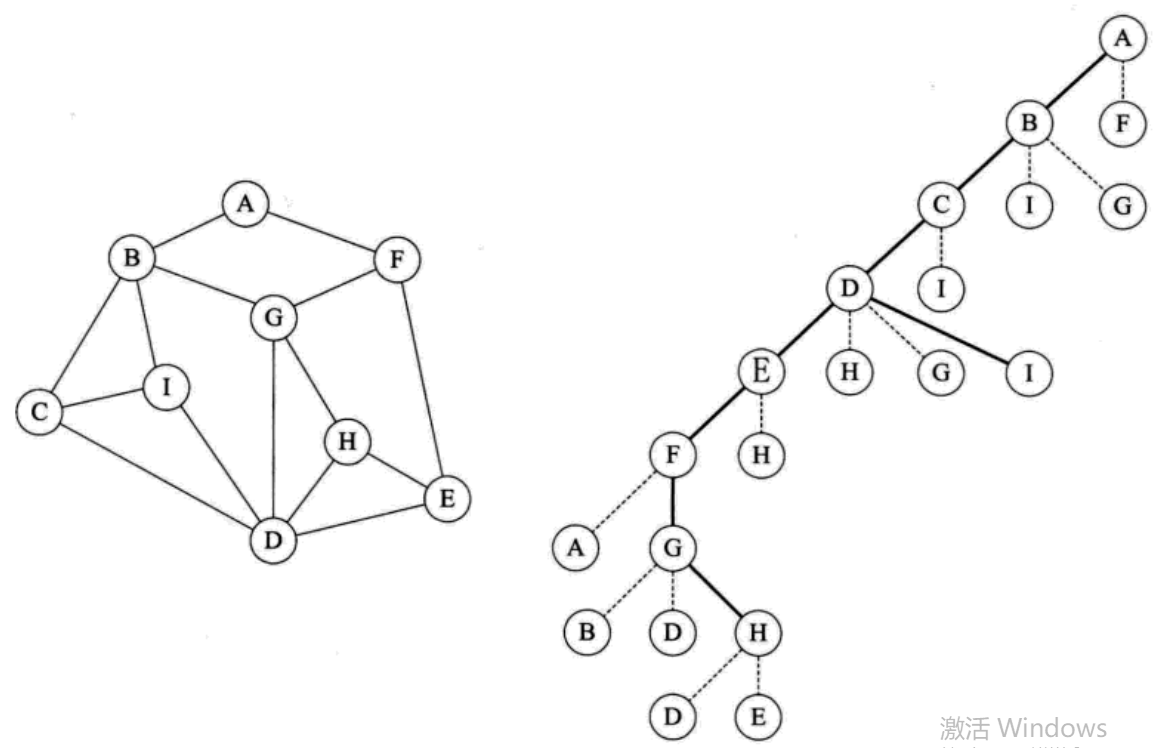
1 深度优先遍历
深度优先遍历,也有称为深度优先搜索,简称 DFS。它从图中某个顶点 V 出发,访问此顶点,然后从 V 的未被访问的邻接点出发深度优先遍历图,直至图中所有和 V 有路径相通的顶点都被访问到。
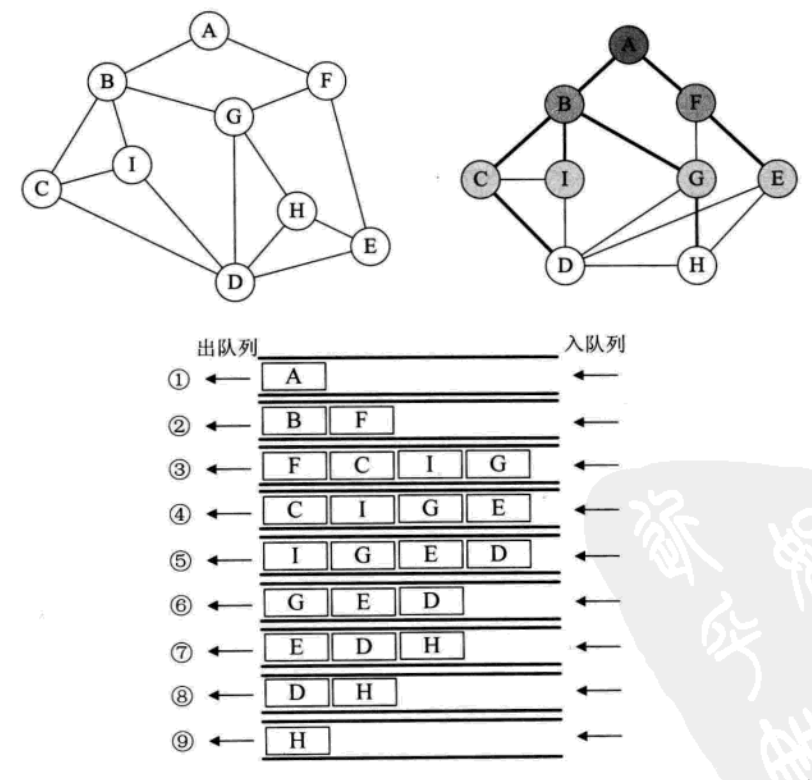
2 广度优先遍历
广度优先遍历,又称为广度优先搜索,简称 BFS。
对比图的深度优先遍历和广度优先遍历算法,它们在时间复杂度上是一样的,不同之处仅仅在于对顶点访问的顺序不同。可见两者在全图遍历上是没有优劣之分的,只是视不同的情况选择不同的算法。