BFPRT算法是解决从n个数中选择第k大或第k小的数这个经典问题的著名算法，但很多人并不了解其细节。本文将首先介绍求解这个第k小数字问题的几个思路，然后重点介绍在最坏情况下复杂度仍然为O(n)的BFPRT算法。
一 基本思路
关于选择第k小的数字有许多方法，其效率和复杂度各不一样，可以根据实际情况进行选择。
- 将n个数排序(比如快速排序或归并排序)，选取排序后的第k个数，时间复杂度为O(nlogn)。使用STL函数sort可以大大减少编码量。
- 将方法1中的排序方法改为线性时间排序算法(如基数排序或计数排序)，时间复杂度为O(n)。但线性时间排序算法使用限制较多，不常使用。
- 维护一个k个元素的最大堆，存储当前遇到的最小的k个数，时间复杂度为O(nlogk)。这种方法同样适用于海量数据的处理。
- 部分的选择排序，即把最小的放在第1位，第二小的放在第2位，直到第k位为止，时间复杂度为O(kn)。实现非常简单。
- 部分的快速排序（快速选择算法），每次划分之后判断第k个数在左右哪个部分，然后递归对应的部分，平均时间复杂度为O(n)。但最坏情况下复杂度为O(n^2)。
- BFPRT算法，修改快速选择算法的主元选取规则，使用中位数的中位数作为主元，最坏情况下时间复杂度为O(n)。
二 快速选择算法
快速选择算法就是修改之后的快速排序算法，前面快速排序的实现与应用这篇文章中讲了它的原理和实现。
其主要思想就是在快速排序中得到划分结果之后，判断要求的第k个数是在划分结果的左边还是右边，然后只处理对应的那一部分，从而达到降低复杂度的效果。
在快速排序中，平均情况下数组被划分成相等的两部分，则时间复杂度为T(n)=2*T(n/2)+O(n)，可以解得T(n)=nlogn。
在快速选择中，平均情况下数组也是分成相等的两部分，但是只处理其中一部分，于是T(n)=T(n/2)+O(n)，可以解得T(n)=O(n)。
但是两者在最坏情况下的时间复杂度均为O(n^2)，出现在每次划分之后左右总有一边为空的情况下。为了避免这个问题，需要谨慎地选取划分的主元，一般的方法有：
- 固定选择首元素或尾元素作为主元。
- 随机选择一个元素作为主元。
- 三数取中，选择三个数的中位数作为主元。一般是首尾数，再加中间的一个数或者随机的一个数。
============================================================
通常，我们需要在一大堆数中求前K大的数，或者求前K小的。比如在搜索引擎中求当天用户点击次数排名前10000的热词；在文本特征选择中求IF-IDF值按从大到小排名前K个的等等问题，都涉及到一个核心问题，即TOP-K问题。
通常来说，TOP-K问题可以先对所有数进行快速排序，然后取前K大的即可。但是这样做有两个问题。
（1）快速排序的平均复杂度为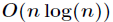
，但最坏时间复杂度为
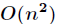，不能始终保证较好的复杂度。
（2）我们只需要前K大的，而对其余不需要的数也进行了排序，浪费了大量排序时间。
除这种方法之外，堆排序也是一个比较好的选择，可以维护一个大小为K的堆，时间复杂度为
。
我们的目的是求前K大的或者前K小的元素，实际上有一个比较好的算法，叫做BFPTR算法，又称为中位数的中位数算法，它的最坏时间复杂度为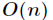
，它是由Blum、Floyd、Pratt、Tarjan、Rivest 提出。
该算法的思想是修改快速选择算法的主元选取方法，提高算法在最坏情况下的时间复杂度。我们先来看看快速排序是如何进行的。
一趟快速排序的过程如下
（1）先从序列中选取一个数作为基准数。
（2）将比这个数大的数全部放到它的右边，把小于或者等于它的数全部放到它的左边。
一趟快速排序也叫做Partion，即将序列划分为两部分，一部分比基准数小，另一部分比基准数大，然后再进行分治过程，因为每一次Partion不一定都能保证划分得很均匀，所以最坏情况下的时间复杂度不能保证总是为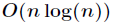
。
对于Partion过程，通常有两种方法：
（1）两个指针从首尾向中间扫描（双向扫描）
这种方法可以用挖坑填数来形容，比如
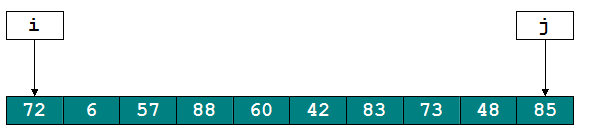
初始化：i = 0; j = 9; pivot = a[0];
现在a[0]保存到了变量pivot中了，相当于在数组a[0]处挖了个坑，那么可以将其它的数填到这里来。从j开始向前找一个小于或者等于pivot的数，即将a[8]填入a[0]，但a[8]又形成了一个新坑，再从i开始向后找一个大于pivot的数，即a[3]填入a[8]，那么a[3]又形成了一个新坑......
就这样，直到i==j才停止，最终得到结果如下
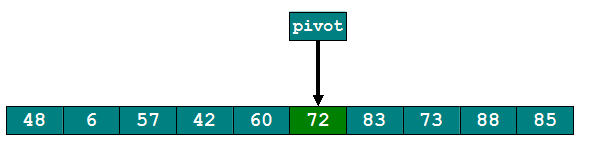
上述过程就是一趟快速排序。
代码：
#include <iostream>
#include <string.h>
#include <stdio.h>
#include <algorithm>
#include <time.h>
using namespace std;
const int N = 10005;
int Partion(int a[], int l, int r)
{
int i = l;
int j = r;
int pivot = a[l];
while (i < j)
{
while (a[j] >= pivot && i < j)
j--;
a[i] = a[j];
while (a[i] <= pivot && i < j)
i++;
a[j] = a[i];
}
a[i] = pivot;
return i;
}
void QuickSort(int a[], int l, int r)
{
if (l < r)
{
int k = Partion(a, l, r);
QuickSort(a, l, k - 1);
QuickSort(a, k + 1, r);
}
}
int a[N];
int main()
{
int n;
while (cin >> n)
{
for (int i = 0; i < n; i++)
cin >> a[i];
QuickSort(a, 0, n - 1);
for (int i = 0; i < n; i++)
cout << a[i] << " ";
cout << endl;
}
return 0;
}（2）两个指针一前一后逐步向前扫描（单向扫描）
代码：
#include <iostream>
#include <string.h>
#include <stdio.h>
using namespace std;
const int N = 10005;
int Partion(int a[], int l, int r)
{
int i = l - 1;
int pivot = a[r];
for(int j = l; j < r; j++)
{
if(a[j] <= pivot)
{
i++;
swap(a[i], a[j]);
}
}
swap(a[i + 1], a[r]);
return i + 1;
}
void QuickSort(int a[], int l, int r)
{
if(l < r)
{
int k = Partion(a, l, r);
QuickSort(a, l, k - 1);
QuickSort(a, k + 1, r);
}
}
int a[N];
int main()
{
int n;
while(cin >> n)
{
for(int i = 0; i < n; i++)
cin >> a[i];
QuickSort(a, 0, n - 1);
for(int i = 0; i < n; i++)
cout << a[i] << " ";
cout << endl;
}
return 0;
} 实际上基于双向扫描的快速排序要比基于单向扫描的快速排序算法快很多。接下来，我们学习BFPTR算法的原理。
在BFPTR算法中，仅仅是改变了快速排序Partion中的pivot值的选取，在快速排序中，我们始终选择第一个元素或者最后一个元素作为pivot，而在BFPTR算法中，每次选择五分中位数的中位数作为pivot，这样做的目的就是使得划分比较合理，从而避免了最坏情况的发生。算法步骤如下：
（1）将输入数组的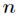
个元素划分为
组，每组5个元素，且至多只有一个组由剩下的
个元素组成。
（2）寻找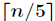
个组中每一个组的中位数，首先对每组的元素进行插入排序，然后从排序过的序列中选出中位数。
（3）对于（2）中找出的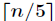
个中位数，递归进行步骤（1）和（2），直到只剩下一个数即为这
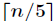个元素的中位数，找到中位数后并找到对应的下标
。
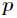（4）进行Partion划分过程，Partion划分中的pivot元素下标为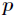
。
（5）进行高低区判断即可。
本算法的最坏时间复杂度为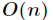
，值得注意的是通过BFPTR算法将数组按第K小（大）的元素划分为两部分，而这高低两部分不一定是有序的，通常我们也不需要求出顺序，而只需要求出前K大的或者前K小的。
另外注意一点，求第K大就是求第n-K+1小，这两者等价。TOP K问题在工程中有重要应用，所以很有必要掌握。
代码：
#include <iostream>
#include <string.h>
#include <stdio.h>
#include <time.h>
#include <algorithm>
using namespace std;
const int N = 10005;
int a[N];
//插入排序
void InsertSort(int a[], int l, int r)
{
for(int i = l + 1; i <= r; i++)
{
if(a[i - 1] > a[i])
{
int t = a[i];
int j = i;
while(j > l && a[j - 1] > t)
{
a[j] = a[j - 1];
j--;
}
a[j] = t;
}
}
}
//寻找中位数的中位数
int FindMid(int a[], int l, int r)
{
if(l == r) return a[l];
int i = 0;
int n = 0;
for(i = l; i < r - 5; i += 5)
{
InsertSort(a, i, i + 4);
n = i - l;
swap(a[l + n / 5], a[i + 2]);
}
//处理剩余元素
int num = r - i + 1;
if(num > 0)
{
InsertSort(a, i, i + num - 1);
n = i - l;
swap(a[l + n / 5], a[i + num / 2]);
}
n /= 5;
if(n == l) return a[l];
return FindMid(a, l, l + n);
}
//寻找中位数的所在位置
int FindId(int a[], int l, int r, int num)
{
for(int i = l; i <= r; i++)
if(a[i] == num)
return i;
return -1;
}
//进行划分过程
int Partion(int a[], int l, int r, int p)
{
swap(a[p], a[l]);
int i = l;
int j = r;
int pivot = a[l];
while(i < j)
{
while(a[j] >= pivot && i < j)
j--;
a[i] = a[j];
while(a[i] <= pivot && i < j)
i++;
a[j] = a[i];
}
a[i] = pivot;
return i;
}
int BFPTR(int a[], int l, int r, int k)
{
int num = FindMid(a, l, r); //寻找中位数的中位数
int p = FindId(a, l, r, num); //找到中位数的中位数对应的id
int i = Partion(a, l, r, p);
int m = i - l + 1;
if(m == k) return a[i];
if(m > k) return BFPTR(a, l, i - 1, k);
return BFPTR(a, i + 1, r, k - m);
}
int main()
{
int n, k;
scanf("%d", &n);
for(int i = 0; i < n; i++)
scanf("%d", &a[i]);
scanf("%d", &k);
printf("The %d th number is : %d
", k, BFPTR(a, 0, n - 1, k));
for(int i = 0; i < n; i++)
printf("%d ", a[i]);
puts("");
return 0;
}
/**
10
72 6 57 88 60 42 83 73 48 85
5
*/ 关于本算法最坏时间复杂度为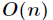
的证明可以参考《算法导论》9.3节，即112页，有详细分析。
原文链接：https://blog.csdn.net/wyq_tc25/article/details/51801885