干草塔

干草塔

给出一个长度为n的正整数序列({a_i}),求将其划分成经可能多的区间的数目，并保证任意一个区间的数字和大于它下一个相邻的区间里数字之和，(nleq 10^5)。

解

首先贪心猜测结论，第一个区间划分的长度最小是最优解

---

证明：假设不是

那么存在一种方案，第一个区间划分的比它长，还比他优，如下图(序列抽象化成了一个矩形，竖线表示两区间之间的边界)

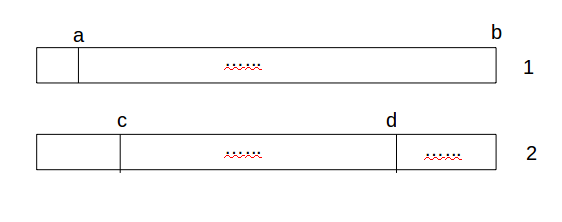
显然可以在方案2中可以找到一个位置d，使c-d中划分的区间数同方案1的位置a-b相同，易知a-b完全包含c-d，因此必然c-d中会存在一个区间被a-b完全包含，假设不成立，必然c-d的每个区间正上方都有方案1中的竖线，如下图

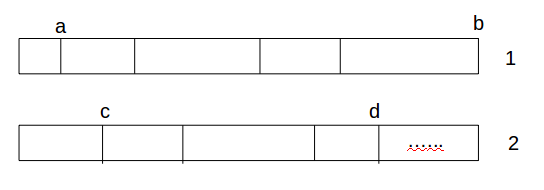
这样必然会导致a-b中区间划分的段数大于c-d中区间划分的段数，故矛盾。

于是寻找这个位置，如下图，即a-b完全包含c-d

此时我们只需要把d以后的分派方案复制给1,既可以让1和2一样优秀，于是矛盾，从而得证。

---

因此自然想到设倒推，设(f_i)表示从第i个数到第n个数划分的最大区间数的第一段区间的数字之和，显然有,设(s_i)为(a_isim a_n)的数字和。

[f_i=min_{i<jleq n,s_i-s_jgeq f_j}{s_i-s_j} ]

注意到(s_i)单调递减，考虑单调队列，原转移方程可以写作

[f_i=s_i+min_{i<jleq n,s_igeq f_j+s_j}{-s_j} ]

于是不难得知，(s_i)单调递减意味着决策集合，必然在不断扩大，不会缩小，我们只要维护什么决策点可以被计算，而最优解用一个变量替代即可，此时只需要维护一个(f_j+s_j)单调递增的单调队列,队列里面储存决策点，记队首决策点j，对于队首操作，只要看其(f_j+s_j)与(s_i)的大小决定是否弹出队首，如果被弹出，用其(-s_j)值与最优解比较大小即可，而记队尾决策点为k，至于进入新的决策点i，如果不能维护单调性，i不但先可以被决策，而且结果更优（(-s_i)单调递增），于是k应该被删去。

转移时顺便维护区间数即可，时间复杂度显然(O(n))。

参考代码：

#include <iostream>
#include <cstdio>
#define il inline
#define ri register
#define Size 100010
using namespace std;
int s[Size],h[Size],f[Size],
    T[Size],L,R,D;
il void read(int&);
int main(){
    int n;read(n);
    for(int i(1);i<=n;++i)read(s[i]);
    for(int i(n);i;--i)s[i]+=s[i+1];
    L=1,R=0,D=n+1;
    for(int i(n);i;--i){
        while(L<=R&&f[T[L]]+s[T[L]]<=s[i]){
            if(-s[T[L]]<-s[D])D=T[L];++L;
        }f[i]=s[i]-s[D],h[i]=h[D]+1;
        while(L<=R&&f[i]+s[i]<=f[T[R]]+s[T[R]])--R;
        T[++R]=i;
    }printf("%d",h[1]);
    return 0;
}
il void read(int &x){
    x&=0;ri char c;while(c=getchar(),c<'0'||c>'9');
    while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
}