给定某空间中(直线空间或平面空间)n个点,请找出它们中的最近点对。你需要完成下列任务:
1、随机产生或手工输入n个点的坐标。
2、输出最近的两个点的坐标。
3、算法尽可能效率高。
解决方案:
针对问题,主要包括两个方面的问题,一是在直线空间求最近点对,二是在平面空间求最近点对。具体解决办法如下:
(1)直线空间求最近点对问题
求最近点对如果直接用蛮力法,即有n个点,从第一个点开始依次算出两点直接的距离,进行大小比较,求出最小值,其时间效率为O(n^2)。那有没有效率更高一点的办法呢?结果当然是有的,那就是采用迭代法(时间效率为O(n*logn),先找出一组点中的中间点,使得在中间点左边的x坐标小于中间点x坐标,中间点右边的x坐标大于中间点x坐标,分成左右两组,用第一组左边组X最大值与右边组X最小值相减即得当前最短距离,在依次迭代,最后递归合并求出最终最短距离。
分治法方案具体代码如下:
package com.liuzhen.ex_two;
public class ClosestPionts {
//初始化一个随机数组
public static int[] initializationArray(int n){
int[] result = new int[n];
for(int i = 0;i < n;i++)
result[i] = (int)(Math.random()*1000); //采用随机函数随机生成1~1000之间的数
return result;
}
//返回数组中最大值
public static int getArrayMax(int a[] , int first , int end){
int max = a[first];
for(int i = first;i < end;i++){
if(max < a[i])
max = a[i];
}
return max;
}
//返回数组中最小值
public static int getArrayMin(int a[] , int first , int end){
int min = a[first];
for(int i = first;i < end;i++){
if(min > a[i])
min = a[i];
}
return min;
}
//交换数组a[n]中两个数的值
public static void swapArray(int a[] , int i , int j){
int temp = a[i];
a[i] = a[j];
a[j] = temp;
}
//采用分治法将数组a[n]分成两组,满足a[n1]<m,a[n2]>m(其中n1+n2 = n)
public static int divideArray(int a[],int first,int end){
int max = getArrayMax(a,first,end);
int min = getArrayMin(a,first,end);
double m = (max + min)/2.0;
//System.out.println("分治法算出中位数m:"+m);
int i = first , j = end-1;
//int a1 = 0;
for( ;i+1 <= j;){
while(a[i] < m && i+1 <= j)
i++;
while(a[j] > m && i+1 <= j)
j--;
// a1++;
// System.out.println("第"+a1+"此交换时a[i] = "+a[i]+" i = "+i+" a[j] = "+a[j]+" j = "+j);
swapArray(a,i,j); //a[i]大于m的值与a[j]小于m的值进行交换,但数组的位置不变
}
//System.out.println("分组后,返回的序号j值是:"+(j));
return j;
}
//采用递归法合并最短距离值,返回最短距离的点
public static int[] getMinDistancePoint(int a[] , int result[],int n ,int first , int end) {
if(end-first <= 1){ //递归终止条件
return result;
}
int j = divideArray(a,first,end);
int minDistance = result[1] - result[0]; //最短距离两点之间的距离大小
if(minDistance > getArrayMin(a,j,end)-getArrayMax(a,first,j))
{
result[0] = getArrayMax(a,first,j); //最短距离两点中数值最小的点
result[1] = getArrayMin(a,j,end); //最短距离两点中数值最小的点
}
int result_one[] = getMinDistancePoint(a,result,2,first,j); //递归
int minDistance_one = result_one[1] - result_one[0];
int result_two[] = getMinDistancePoint(a,result,2,j,end); //递归
int minDistance_two = result_two[1] - result_two[0];
if(minDistance > minDistance_one)
result = result_one;
if(minDistance > minDistance_two)
result = result_two;
return result;
}
public static void main(String[] args){
int a[] = new int[10];
int b[] = new int[2];
b[0] = 0;
b[1] = 100;
a = initializationArray(15);
String one_text = "";
for(int i = 0;i < 15;i++){
one_text += "直线随机点Point["+i+"] = "+a[i]+"
";
//System.out.print("数组a["+i+"] = "+a[i]+"
");
}
int result[] = getMinDistancePoint(a,b,2,0,15);
//System.out.println("result[0] = "+result[0]+"
"+"result[1] = "+result[1]);
one_text += "最短距离点对第1点result[0] = "+result[0]+"
"+"最短距离点对第2点result[1] = "+result[1];
System.out.print(one_text);
}
}
结果为
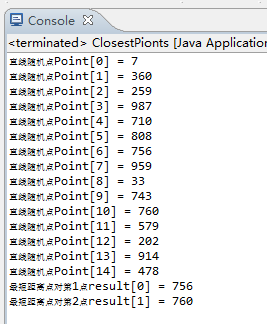
(2)平面空间求最近点对问题
平面空间教直线空间求最近点对问题就变得更加复杂一点,在此就只讨论使用蛮力法求解平面空间求最近点对问题,如有对平面使用分治法求解感兴趣的同学请看本文末尾参考资料2。
蛮力法方案具体如下:
由于是在平面,点坐标表示为(x,y),在此先创建一个Point类(方便后续功能类实现):
package com.liuzhen.ex_two;
public class Point {
private int x; //平面点中的x坐标
private int y; //平面点中的y坐标
//未给类对象初始化时,默认点坐标为(0,0)
public Point(){
this.x = 0;
this.y = 0;
}
public Point(int x,int y){
this.x = x;
this.y = y;
}
//给x赋值
public void setX(int x){
this.x = x;
}
//给y赋值
public void setY(int y){
this.y = y;
}
//返回x
public int getX(){
return x;
}
//返回y
public int getY(){
return y;
}
}
package com.liuzhen.ex_two;
public class ClosestPionts {//平面中求两点最短距离问题解法
//初始化一个平面中n个点,具体点的坐标值随机生成
public static Point[] initializationPlaneArray(int n){
Point result[] = new Point[n];
for(int i = 0;i < n;i++){
int x1 = (int)(Math.random()*50); //采用随机函数随机生成1~100之间的数
int y1 = (int)(Math.random()*50);
result[i] = new Point(x1,y1);
}
return result;
}
//蛮力法直接求平面中两点之间的最短距离,返回最短距离的两点坐标
public static Point[] getMinDistancePlanePoint(Point a[],int n){
Point result[] = new Point[2];
double min = 10000; //定义两点之间最短距离变量,初始化为10000
for(int i = 0;i < n;i++){
int x = a[i].getX();
int y = a[i].getY();
for(int j = i+1;j < n;j++){
int x1 = a[j].getX();
int y1 = a[j].getY();
long minSquare = (x-x1)^2 + (y-y1)^2; //利用数学中求两点之间距离公式,得到两点之间距离的平方
double min1 = Math.sqrt(minSquare); //求两点之间距离的中间变量
if(min > min1){
min = min1;
result[0] = new Point(x,y);
result[1] = new Point(x1,y1);
}
}
}
return result;
}
public static void main(String[] args){
String two_text = "";
Point c[] = initializationPlaneArray(15);
for(int i = 0;i < 15;i++){
two_text += "Point["+i+"] = "+"("+c[i].getX()+","+c[i].getY()+")"+"
";
//System.out.println("c["+i+"] = "+"("+c[i].getX()+","+c[i].getY()+")");
}
//System.out.println(two_text);
Point back[] = getMinDistancePlanePoint(c,15);
for(int i = 0;i < 2;i++){
two_text += "距离最短的两点第"+(i+1)+"个点坐标是:"+"("+back[i].getX()+","+back[i].getY()+")"+"
";
//System.out.println("距离最短的两点第"+(i+1)+"个点坐标是:"+"("+back[i].getX()+","+
//back[i].getY()+")");
}
System.out.println(two_text);
}
}
结果为
