1 问题描述
1.1实验题目
设M1和M2是两个n×n的矩阵,设计算法计算M1×M2 的乘积。
1.2实验目的
(1)提高应用蛮力法设计算法的技能;
(2)深刻理解并掌握分治法的设计思想;
(3)理解这样一个观点:用蛮力法设计的算法,一般来说,经过适度的努力后,都可以对其进行改进,以提高算法的效率。
1.3实验要求
(1)设计并实现用BF(Brute-Force,即蛮力法)方法求解矩阵相乘问题的算法;
(2)设计并实现用DAC(Divide-And-Conquer,即分治法)方法求解矩阵相乘问题的算法;
(3)以上两种算法的输入既可以手动输入,也可以自动生成;
(4)对上述两个算法进行时间复杂性分析,并设计实验程序验证分析结果;
(5)设计可供用户选择算法的交互式菜单(放在相应的主菜单下)。
2 解决方案
2.1 分治法原理简述
分治法的设计思想是:将一个难以直接解决的大问题,分割成一些规模较小的相同问题,以便各个击破,分而治之。
分治策略是:对于一个规模为n的问题,若该问题可以容易地解决(比如说规模n较小)则直接解决,否则将其分解为k个规模较小的子问题,这些子问题互相独立且与原问题形式相同,递归地解这些子问题,然后将各子问题的解合并得到原问题的解。这种算法设计策略叫做分治法。
如果原问题可分割成k个子问题,1<k≤n ,且这些子问题都可解并可利用这些子问题的解求出原问题的解,那么这种分治法就是可行的。由分治法产生的子问题往往是原问题的较小模式,这就为使用递归技术提供了方便。在这种情况下,反复应用分治手段,可以使子问题与原问题类型一致而其规模却不断缩小,最终使子问题缩小到很容易直接求出其解。这自然导致递归过程的产生。分治与递归像一对孪生兄弟,经常同时应用在算法设计之中,并由此产生许多高效算法。
分治法所能解决的问题一般具有以下几个特征:
-
该问题的规模缩小到一定的程度就可以容易地解决
-
该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质。
-
利用该问题分解出的子问题的解可以合并为该问题的解;
-
该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题。
2.2 分治法求解矩阵相乘原理
首先了解一下传统计算矩阵相乘的原理:

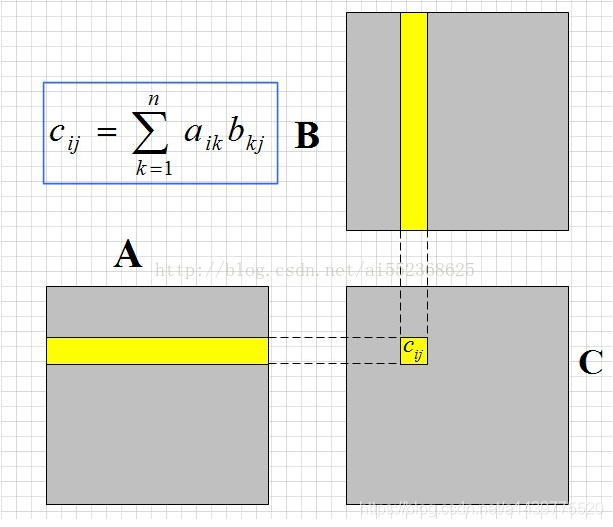
其次,看一下优化后的矩阵相乘法原理:

最后,看一下本文利用分治法求解矩阵相乘的原理(PS:本文求解其效率不是最高,主要是体验一下分治法,重点在于分治法):
注意:使用分治法求解两个nxn阶矩阵相乘,其中n值为2的幂值,否则只能使用蛮力法计算。


本文具体源码主要根据以上分块矩阵方法,先分块(即使用分治法),然后递归求解。
2.3 具体实现源码
package com.liuzhen.dac;
public class Matrix {
//初始化一个随机nxn阶矩阵
public static int[][] initializationMatrix(int n){
int[][] result = new int[n][n];
for(int i = 0;i < n;i++){
for(int j = 0;j < n;j++){
result[i][j] = (int)(Math.random()*10); //采用随机函数随机生成1~10之间的数
}
}
return result;
}
//蛮力法求解两个nxn和nxn阶矩阵相乘
public static int[][] BruteForce(int[][] p,int[][] q,int n){
int[][] result = new int[n][n];
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
result[i][j] = 0;
for(int k=0;k<n;k++){
result[i][j] += p[i][k]*q[k][j];
}
}
}
return result;
}
//分治法求解两个nxn和nxn阶矩阵相乘
public static int[][] DivideAndConquer(int[][] p,int[][] q,int n){
int[][] result = new int[n][n];
//当n为2时,返回矩阵相乘结果
if(n == 2){
result = BruteForce(p,q,n);
return result;
}
//当n大于3时,采用采用分治法,递归求最终结果
if(n > 2){
int m = n/2;
int[][] p1 = QuarterMatrix(p,n,1);
int[][] p2 = QuarterMatrix(p,n,2);
int[][] p3 = QuarterMatrix(p,n,3);
int[][] p4 = QuarterMatrix(p,n,4);
// System.out.println();
// System.out.print("矩阵p1值为:");
// PrintfMatrix(p1,m);
// System.out.println();
// System.out.print("矩阵p2值为:");
// PrintfMatrix(p2,m);
// System.out.println();
// System.out.print("矩阵p3值为:");
// PrintfMatrix(p3,m);
// System.out.println();
// System.out.print("矩阵p4值为:");
// PrintfMatrix(p4,m);
int[][] q1 = QuarterMatrix(q,n,1);
int[][] q2 = QuarterMatrix(q,n,2);
int[][] q3 = QuarterMatrix(q,n,3);
int[][] q4 = QuarterMatrix(q,n,4);
int[][] result1 = QuarterMatrix(result,n,1);
int[][] result2 = QuarterMatrix(result,n,2);
int[][] result3 = QuarterMatrix(result,n,3);
int[][] result4 = QuarterMatrix(result,n,4);
result1 = AddMatrix(DivideAndConquer(p1,q1,m),DivideAndConquer(p2,q3,m),m);
result2 = AddMatrix(DivideAndConquer(p1,q2,m),DivideAndConquer(p2,q4,m),m);
result3 = AddMatrix(DivideAndConquer(p3,q1,m),DivideAndConquer(p4,q3,m),m);
result4 = AddMatrix(DivideAndConquer(p3,q2,m),DivideAndConquer(p4,q4,m),m);
result = TogetherMatrix(result1,result2,result3,result4,m);
}
return result;
}
//获取矩阵的四分之一,并决定返回哪一个四分之一
public static int[][] QuarterMatrix(int[][] p,int n,int number){
int rows = n/2; //行数减半
int cols = n/2; //列数减半
int[][] result = new int[rows][cols];
switch(number){
case 1 :
{
// result = new int[rows][cols];
for(int i=0;i<rows;i++){
for(int j=0;j<cols;j++){
result[i][j] = p[i][j];
}
}
break;
}
case 2 :
{
// result = new int[rows][n-cols];
for(int i=0;i<rows;i++){
for(int j=0;j<n-cols;j++){
result[i][j] = p[i][j+cols];
}
}
break;
}
case 3 :
{
// result = new int[n-rows][cols];
for(int i=0;i<n-rows;i++){
for(int j=0;j<cols;j++){
result[i][j] = p[i+rows][j];
}
}
break;
}
case 4 :
{
// result = new int[n-rows][n-cols];
for(int i=0;i<n-rows;i++){
for(int j=0;j<n-cols;j++){
result[i][j] = p[i+rows][j+cols];
}
}
break;
}
default:
break;
}
return result;
}
//把均分为四分之一的矩阵,聚合成一个矩阵,其中矩阵a,b,c,d分别对应原完整矩阵的四分中1、2、3、4
public static int[][] TogetherMatrix(int[][] a,int[][] b,int[][] c,int[][] d,int n){
int[][] result = new int[2*n][2*n];
for(int i=0;i<2*n;i++){
for(int j=0;j<2*n;j++){
if(i<n){
if(j<n){
result[i][j] = a[i][j];
}
else
result[i][j] = b[i][j-n];
}
else{
if(j<n){
result[i][j] = c[i-n][j];
}
else{
result[i][j] = d[i-n][j-n];
}
}
}
}
return result;
}
//求两个矩阵相加结果
public static int[][] AddMatrix(int[][] p,int[][] q,int n){
int[][] result = new int[n][n];
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
result[i][j] = p[i][j]+q[i][j];
}
}
return result;
}
//控制台输出矩阵
public static void PrintfMatrix(int[][] matrix,int n){
for(int i=0;i<n;i++){
System.out.println();
for(int j=0;j<n;j++){
System.out.print(" ");
System.out.print(matrix[i][j]);
}
}
}
public static void main(String args[]){
int[][] p = initializationMatrix(8);
int[][] q = initializationMatrix(8);
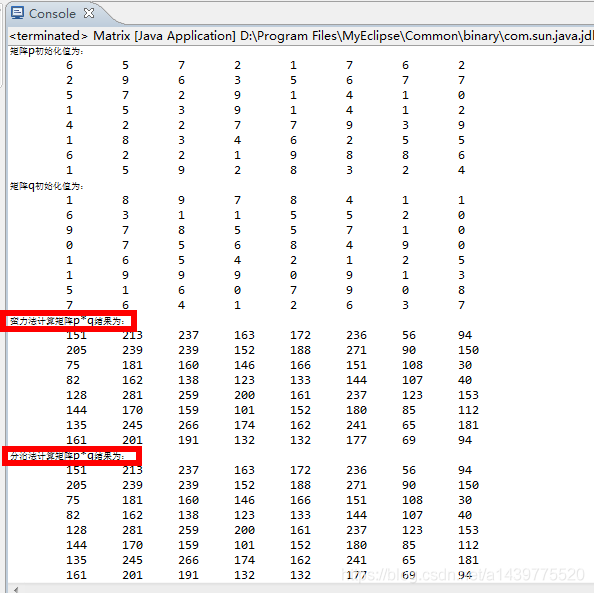
System.out.print("矩阵p初始化值为:");
PrintfMatrix(p,8);
System.out.println();
System.out.print("矩阵q初始化值为:");
PrintfMatrix(q,8);
int[][] bf_result = BruteForce(p,q,8);
System.out.println();
System.out.print("蛮力法计算矩阵p*q结果为:");
PrintfMatrix(bf_result,8);
int[][] dac_result = DivideAndConquer(p,q,8);
System.out.println();
System.out.print("分治法计算矩阵p*q结果为:");
PrintfMatrix(dac_result,8);
}
}
2.4 运算结果截图