[问题描述]
根据给定的若干权值可以构造出一颗哈夫曼树。构造的哈夫曼树可能不唯一,但是按照下面的选取原则所构造出来的哈夫曼树应该是唯一的。
(1)每次选取优先级最低的两个结点,优先级最低的作为左子树,优先级高的作为右子树;
(2)结点优先级大小的比较首先比较它们的权值,权值大的优先级高,权值小的优先级低,权值相等的按照位置关系来比较,位置在前面的优先级低,位置在后面的优先级高。
(3)增加的新结点位置依次往后。
根据你所构造的哈夫曼树来设计每个权值的哈夫曼编码(左子树0右子树1),并计算该哈夫曼树的WPL值。
[输入]
包含多组数据
每组数据包含2行,第一行输入权值个数n(0<n<20),第2行为顺序输入的n个权值,均为整数(小于100),
[输出]
对于每组数据,输出n+1行,前面n行为每个权值所对应的赫夫曼编码(按照输入顺序给出),第n+1行用来输出你所构造的哈夫曼树的WPL值。
[样例输入]
5
11 4 2 5 7
6
2 3 4 7 8 9
[样例输出]
11
011
010
00
10
64
1110
1111
110
00
01
10
80
PS:
他这个是特别版的哈夫曼树,相同的权值时,位置靠左面的会小,
所以你查询的时候,先靠左查询,其他不懂得在评论
哈夫曼树相关的几个名词
路径:在一棵树中,一个结点到另一个结点之间的通路,称为路径。图 1 中,从根结点到结点 a 之间的通路就是一条路径。
路径长度:在一条路径中,每经过一个结点,路径长度都要加 1 。例如在一棵树中,规定根结点所在层数为1层,那么从根结点到第 i 层结点的路径长度为 i - 1 。图 1 中从根结点到结点 c 的路径长度为 3。
结点的权:给每一个结点赋予一个新的数值,被称为这个结点的权。例如,图 1 中结点 a 的权为 7,结点 b 的权为 5。
结点的带权路径长度:指的是从根结点到该结点之间的路径长度与该结点的权的乘积。例如,图 1 中结点 b 的带权路径长度为 2 * 5 = 10 。
树的带权路径长度为树中所有叶子结点的带权路径长度之和。通常记作 “WPL” 。例如图 1 中所示的这颗树的带权路径长度为:
WPL = 7 * 1 + 5 * 2 + 2 * 3 + 4 * 3
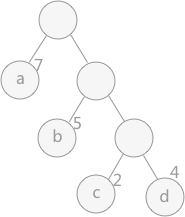
图1 哈夫曼树
什么是哈夫曼树
当用 n 个结点(都做叶子结点且都有各自的权值)试图构建一棵树时,如果构建的这棵树的带权路径长度最小,称这棵树为“最优二叉树”,有时也叫“赫夫曼树”或者“哈夫曼树”。
在构建哈弗曼树时,要使树的带权路径长度最小,只需要遵循一个原则,那就是:权重越大的结点离树根越近。在图 1 中,因为结点 a 的权值最大,所以理应直接作为根结点的孩子结点。
构建哈夫曼树的过程
对于给定的有各自权值的 n 个结点,构建哈夫曼树有一个行之有效的办法:
在 n 个权值中选出两个最小的权值,对应的两个结点组成一个新的二叉树,且新二叉树的根结点的权值为左右孩子权值的和;
在原有的 n 个权值中删除那两个最小的权值,同时将新的权值加入到 n–2 个权值的行列中,以此类推;
重复 1 和 2 ,直到所以的结点构建成了一棵二叉树为止,这棵树就是哈夫曼树。

图 2 哈夫曼树的构建过程
图 2 中,(A)给定了四个结点a,b,c,d,权值分别为7,5,2,4;第一步如(B)所示,找出现有权值中最小的两个,2 和 4 ,相应的结点 c 和 d 构建一个新的二叉树,树根的权值为 2 + 4 = 6,同时将原有权值中的 2 和 4 删掉,将新的权值 6 加入;进入(C),重复之前的步骤。直到(D)中,所有的结点构建成了一个全新的二叉树,这就是哈夫曼树。
import java.util.ArrayList;
import java.util.Collections;
import java.util.Scanner;
public class Demo10哈弗们数 {
public static class TreeNode implements Comparable<TreeNode>{
int val;
boolean bool;
TreeNode left;
TreeNode right;
TreeNode(int x) {
val = x;
}
@Override
public int compareTo(TreeNode o) {
// TODO 自动生成的方法存根
if(this.val>o.val){
return 1;
}
else if(this.val<o.val){
return -1;
}
else {
if(this.bool){
return 1;
}
else if(o.bool){
return -1;
}
}
return 0;
}
}
static TreeNode tree = new TreeNode(0);
static ArrayList<TreeNode> list = new ArrayList<TreeNode>();
static ArrayList<String> list1 = new ArrayList<String>();
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
while(sc.hasNext()){
tree = new TreeNode(0);
list = new ArrayList<TreeNode>();
list1 = new ArrayList<String>();
int sum = 0;
int n = sc.nextInt();
int[] num = new int[n];
for (int i = 0; i < n; i++) {
num[i] = sc.nextInt();
TreeNode tree11 = new TreeNode(num[i]);
list.add(tree11);
}
Collections.sort(list);
// Arrays.sort(num);
madetree();
for (int i = 0; i < num.length; i++) {
findtree(tree, num[i], "");
System.out.println( list1.get(i));
sum+=num[i]*list1.get(i).length();
}
System.out.println(sum);
// System.out.println(list1.size());
}
}
public static void findtree(TreeNode node, int n, String s) {
if (node.val == n && !node.bool) {
list1.add(s);
return;
}
if (node.left != null)
findtree(node.left, n, s + "0");
if (node.right != null)
findtree(node.right, n, s + "1");
return;
}
public static void madetree() {
boolean flag = true;
while (list.size() != 1) {
Collections.sort(list);
// int a = list.get(0);
// int b = list.get(1);
// if (a > b) {
// int temp = a;
// a = b;
// b = temp;
// }
TreeNode treeleft = list.get(0);
TreeNode treeright = list.get(1);
list.remove(0);
list.remove(0);
TreeNode treemid = new TreeNode(treeleft.val+treeright.val);
treemid.left = treeleft;
treemid.right = treeright;
treemid.bool = true;
tree = treemid;
// if (flag) {
// flag = false;
//
// TreeNode treeleft1 = null;
// TreeNode treeright1 = null;
//
// if (treemid.val > tree.val) {
// treeleft1 = tree;
// treeright1 = treemid;
//
// } else {
// treeleft1 = treemid;
// treeright1 = tree;
// }
// TreeNode treemid1 = new TreeNode(tree.val + treemid.val);
// treemid1.left = treeleft1;
// treemid1.right = treeright1;
// treemid1.bool = true;
// if (tree.val != 0) {
// tree = treemid1;
// } else {
// tree = treemid;
// }
// }
list.add(tree);
}
}
}