Java实现 LeetCode 218 天际线问题

218. 天际线问题

城市的天际线是从远处观看该城市中所有建筑物形成的轮廓的外部轮廓。现在，假设您获得了城市风光照片（图A）上显示的所有建筑物的位置和高度，请编写一个程序以输出由这些建筑物形成的天际线（图B）。

Buildings Skyline Contour

每个建筑物的几何信息用三元组 [Li，Ri，Hi] 表示，其中 Li 和 Ri 分别是第 i 座建筑物左右边缘的 x 坐标，Hi 是其高度。可以保证 0 ≤ Li, Ri ≤ INT_MAX, 0 < Hi ≤ INT_MAX 和 Ri - Li > 0。您可以假设所有建筑物都是在绝对平坦且高度为 0 的表面上的完美矩形。

例如，图A中所有建筑物的尺寸记录为：[ [2 9 10], [3 7 15], [5 12 12], [15 20 10], [19 24 8] ] 。

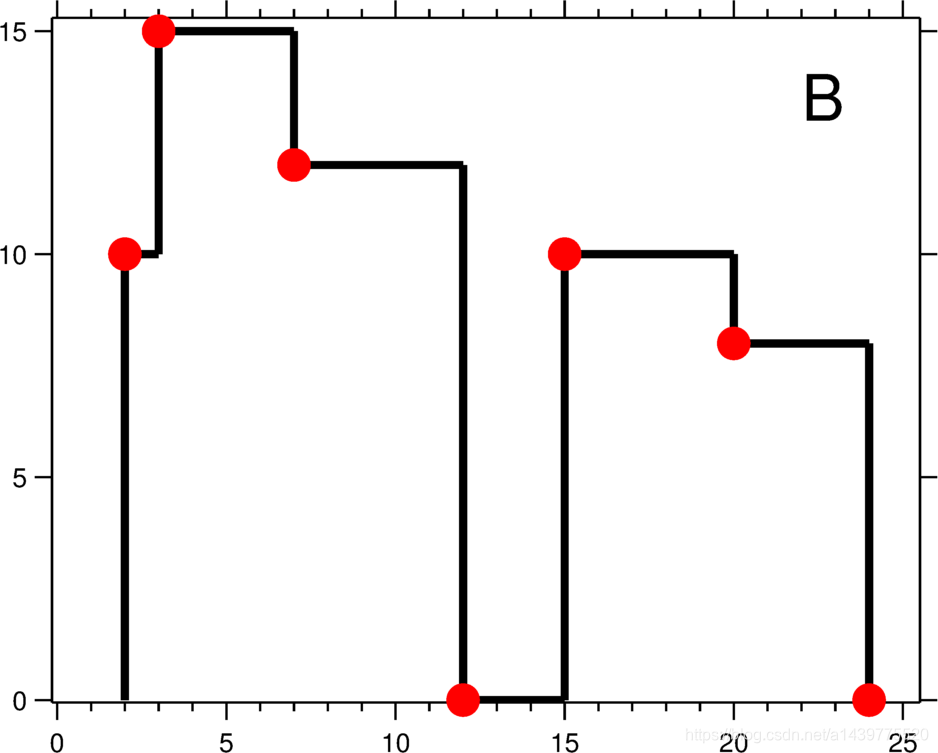
输出是以 [ [x1,y1], [x2, y2], [x3, y3], … ] 格式的“关键点”（图B中的红点）的列表，它们唯一地定义了天际线。关键点是水平线段的左端点。请注意，最右侧建筑物的最后一个关键点仅用于标记天际线的终点，并始终为零高度。此外，任何两个相邻建筑物之间的地面都应被视为天际线轮廓的一部分。

例如，图B中的天际线应该表示为：[ [2 10], [3 15], [7 12], [12 0], [15 10], [20 8], [24, 0] ]。

说明:

任何输入列表中的建筑物数量保证在 [0, 10000] 范围内。
输入列表已经按左 x 坐标 Li 进行升序排列。
输出列表必须按 x 位排序。
输出天际线中不得有连续的相同高度的水平线。例如 […[2 3], [4 5], [7 5], [11 5], [12 7]…] 是不正确的答案；三条高度为 5 的线应该在最终输出中合并为一个：[…[2 3], [4 5], [12 7], …]

class Solution {
   // 线段树 
    public List<List<Integer>> getSkyline(int[][] buildings) {
        int len = buildings.length;
        if (len == 0) return new ArrayList<>();
        return segment(buildings, 0, len - 1);
    }

    private List<List<Integer>> segment(int[][] buildings, int l, int r) {
        // 创建返回值
        List<List<Integer>> res = new ArrayList<>();

        // 找到树底下的结束条件 -> 一个建筑物
        if (l == r) {
            res.add(Arrays.asList(buildings[l][0], buildings[l][2])); // 左上端坐标
            res.add(Arrays.asList(buildings[l][1], 0)); // 右下端坐标
            return res;
        }

        int mid = l + (r - l) / 2; // 取中间值

        // 左边递归
        List<List<Integer>> left = segment(buildings, l, mid);

        // 右边递归
        List<List<Integer>> right = segment(buildings, mid + 1, r);

        // 左右合并

        // 创建left 和 right 的索引位置
        int m = 0, n = 0;
        // 创建left 和 right 目前的高度
        int lpreH = 0, rpreH = 0;
        // 两个坐标
        int leftX, leftY, rightX, rightY;
        while (m < left.size() || n < right.size()) {

            // 当有一边完全加入到res时，则加入剩余的那部分
            if (m >= left.size()) res.add(right.get(n++));
            else if (n >= right.size()) res.add(left.get(m++));

            else { // 开始判断left 和 right
                leftX = left.get(m).get(0); // 不会出现null，可以直接用int类型
                leftY = left.get(m).get(1);
                rightX = right.get(n).get(0);
                rightY = right.get(n).get(1);
                //看我这两个矩形谁靠左
                if (leftX < rightX) {
                    //左面还比以前高，就加左面
                   if (leftY > rpreH) res.add(left.get(m));
                   //左面比右面高，我要加入左面点的以及以前右面的的高度，因为我马上就有新高度了2，10
                   else if (lpreH > rpreH) res.add(Arrays.asList(leftX, rpreH));
                 //  用我左面的高替换我以前右面的高
                    lpreH = leftY;
                    m++;
                } else if (leftX > rightX) {
                   if (rightY > lpreH) res.add(right.get(n));
                   else if (rpreH > lpreH) res.add(Arrays.asList(rightX, lpreH));
                    rpreH = rightY;
                    n++;
                } else { // left 和 right 的横坐标相等
                  if (leftY >= rightY && leftY != (lpreH > rpreH ? lpreH : rpreH)) res.add(left.get(m));
                    else if (leftY <= rightY && rightY != (lpreH > rpreH ? lpreH : rpreH)) res.add(right.get(n));
                    lpreH = leftY;
                    rpreH = rightY;
                    m++;
                    n++;
                }
            }
        }
        return res;
    }

}