结对开发——最大联通子数组的和

一、题目及要求

题目:返回一个二维整数数组中最大联通子数组的和。

要求：

输入一个二维整形数组，数组里有正数也有负数。

求所有子数组的和的最大值。要求时间复杂度为O(n)。

程序要使用的数组放在一个叫 input.txt 的文件中， 文件格式是:

数组的行数,

数组的列数,

每一行的元素

每一个数字都是有符号32位整数，当然，行数和列数都是正整数。

二、设计思想

因为每一个数字都是有符号32位整数，所以选择了long型。从文件中读取，采用c++输入输出流。矩阵中的数是随机生成的，可能会有正有负，所以要首先判断二维数组中哪些位置上的数是正数，利用另一个二维数组记录正数的位置，然后判断哪些数是连通的，我的思路是先判断两个数的行数（列数）是否相同，如果相同，再判断列数（行数）是否相邻，如果相邻即证明两个数连通，计算每个连通块的数值的和，然后再连通不同的块，计算其和，最后比较其中的最大值，即为二维整数数组中最大联通子数组的和。

三、源代码

#include<iostream>
#include<fstream>
using namespace std;

long Max(long n,long a[],long *smark,long *mmark)
{
    long b[100]={0};
    long sum1=0,max1=0,i;
    for(i=0;i<n;i++)
    {
        if(sum1<0)
        {
            sum1=a[i];
        }
        else
        {
            sum1=sum1+a[i];
        }
        b[i]=sum1;
    }
    max1=b[0];
    for(i=0;i<n;i++)
    {
        if (max1<b[i]) 
         {
             max1= b[i];
             *mmark = i;
         }
    }
     for (i = *mmark;i >= 0;i--) 
    {
        if (b[i] == a[i]) 
        {
             *smark = i;
             break;
        }
    }
     return max1;
}

int main()
{
    long m,n,i,j,t2,c[2];
    long sum,smark,mmark;
    long up[100],down[100],t[100];
    long a[100][100],b[100];
	ifstream infile;
    infile.open("input.txt", ios::in);
	  if(infile.is_open() == false)
	  {
         cerr << "open error!" << endl;
         exit(1);
	  }
    
    cout<<"二维数组的行数和列数：";
     for(i=0;i<2;i++) 
     {
	 infile >> c[i];
     
     }          //在显示器上顺序显示个数
	 m=c[0];
	 n=c[1];
	 cout<<m<<" "<<n<<endl;
    cout<<"数组为"<<endl;
    for(i=0;i<m;i++)
    {
        for(j=0;j<n;j++)
        {
            infile>>a[i][j];
			cout<<a[i][j]<<"   ";
        }
		if(j%n==0)
		{
			cout<<endl;
		}
    }
    //把二维数组按行分解为几个一维数组
    for(i=0;i<m;i++)
    {
        for(j=0;j<n;j++)
        {
            b[j]=a[i][j];
        }
        sum=Max(n,b,&smark,&mmark);
        up[i]=smark;                                    
        down[i]=mmark;
        t[i]=sum;

    }
    t2=t[0];
    for(i=0;i+1<m;i++)
    {
        if(up[i]<=down[i+1] && down[i]>=up[i+1])
        {
            t2+=t[i+1];
        }
         for(j=up[i];j<up[i+1];j++)
        {
            if(a[i+1][j]>0) t2+=a[i+1][j];                   //判别独立正数
        }

    }
	 cout<<"最大联通子数组和为";
     cout<<t2<<endl;
	 return 0;

}

四、结果截图

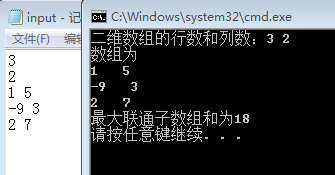
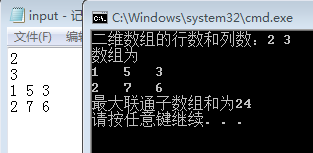
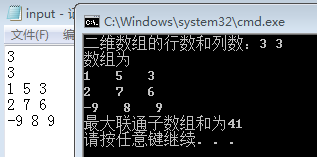
五、项目计划日志

日期&&任务	听课	编写程序	阅读相关书籍	网上查找资料	日总计
周一	100		30	30	160
周二		120	30	30	180
周三		30	30	10	70
周四	100	20	30		150
周五		120	30	30	180
周六		145	30	10	85
周日		200	30
周总计	200	635	210	110	1155

时间记录日志

3/28

日期	开始时间	结束时间	中断时间	净时间	活动	备注
3/28	14：00	15：50	10	100	听课	软件工程上课
	21：04	21:  34	0	30	阅读书籍	《构建之法》
	22：10	22： 40	0	30	网上查找资料	查阅安卓相关资料
3/29	18:00	18:30	0	30	阅读书籍	《构建之法》
	19：00	21：30	20	120	编写程序	结对开发- 安卓APP
	22:  15	22:  45	0	30	网上查找资料	查阅安卓相关资料
3/30	19:  25	20： 00	5	30	编写程序	结对开发- 安卓APP
	22：00	22： 30	0	30	阅读书籍	《构建之法》
	22：40	22： 50	0	10	查找资料	查阅安卓相关资料
3/31	14：00	15:  50	10	100	上课	软件工程上课
	18：26	18： 50	4	20	编写程序	结对开发- 联通版
	22:00	22:30	0	30	阅读书籍	《构建之法》
4/1	14:  00	16:  20	20	120	编写程序	结对开发- 安卓APP
	11：23	12： 00	7	30	网上查找资料	查阅安卓相关资料
	21:00	21:30	0	30	阅读书籍	《构建之法》
4/2	7： 00	7： 30	0	30	阅读书籍	阅读《构建之法》
	10： 00	13： 00	35	145	编写程序	结对开发- 安卓APP
	9:   45	9： 55	0	10	网上查找资料	查阅安卓相关资料
4/3	8：20	12:  00	20	200	编写程序	结对开发-联通版
	15: 23	16： 00	7	30	阅读书籍	阅读《构建之法》

缺陷记录日志

日期	编号	类型	引入阶段	排除阶段	修复时间	备注
3/31	1	20	编码	编译	4	最开始没有定义long型
3/31	2	20	编码	编译	1	文件打开有问题
4/1	3	20	编码	编译	7	当数组长度为0时，无法正常跳出

同组的小伙伴：http://www.cnblogs.com/qizhonh/p/5360641.html