[NOIP2015]运输计划
题目背景
公元 2044 年,人类进入了宇宙纪元。
题目描述
L 国有 n 个星球,还有 n-1 条双向航道,每条航道建立在两个星球之间,这 n-1 条航道连通了 L 国的所有星球。
小 P 掌管一家物流公司,该公司有很多个运输计划,每个运输计划形如:有一艘物
流飞船需要从 ui 号星球沿最快的宇航路径飞行到 vi 号星球去。显然,飞船驶过一条航道 是需要时间的,对于航道 j,任意飞船驶过它所花费的时间为 tj,并且任意两艘飞船之 间不会产生任何干扰。
为了鼓励科技创新,L 国国王同意小 P 的物流公司参与 L 国的航道建设,即允许小 P 把某一条航道改造成虫洞,飞船驶过虫洞不消耗时间。
在虫洞的建设完成前小 P 的物流公司就预接了 m 个运输计划。在虫洞建设完成后, 这 m 个运输计划会同时开始,所有飞船一起出发。当这 m 个运输计划都完成时,小 P 的 物流公司的阶段性工作就完成了。
如果小 P 可以自由选择将哪一条航道改造成虫洞,试求出小 P 的物流公司完成阶段 性工作所需要的最短时间是多少?
输入输出格式
输入格式:
输入文件名为 transport.in。
第一行包括两个正整数 n、m,表示 L 国中星球的数量及小 P 公司预接的运输计划的数量,星球从 1 到 n 编号。
接下来 n-1 行描述航道的建设情况,其中第 i 行包含三个整数 ai, bi 和 ti,表示第
i 条双向航道修建在 ai 与 bi 两个星球之间,任意飞船驶过它所花费的时间为 ti。
接下来 m 行描述运输计划的情况,其中第 j 行包含两个正整数 uj 和 vj,表示第 j个 运输计划是从 uj 号星球飞往 vj 号星球。
输出格式:
输出 共1行,包含1个整数,表示小P的物流公司完成阶段性工作所需要的最短时间。
输入输出格式
输入样例1#:
6 3
1 2 3
1 6 4
3 1 7
4 3 6
3 5 5
3 6
2 5
4 5
输出样例1#:
11
说明
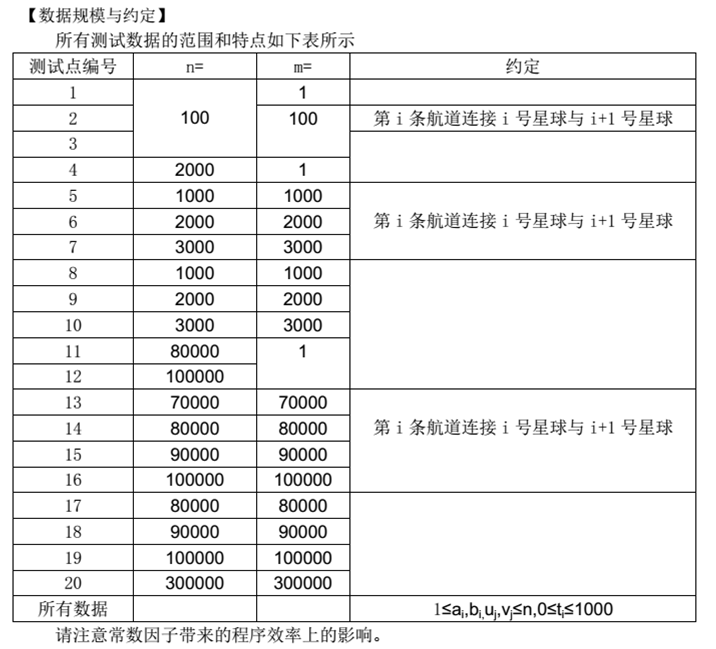
题目大概就是要使一条边的权值变为零,使得选择的所有路径的长度值最大值最小。
考虑二分答案,但这个检验怎么搞啊?
对于一个二分长度mid,先把那些比它长的标记一下记录为num个,之后枚举每一条边,如果覆盖这条边的所有路径数为num,且这条边的权值>=(MAX-mid)。
然后我还是不会搞,所以去看大佬们写的题解,说是要树上差分,我*,这又是什么鬼,今天一定要好好学习一下,就拿这题练手。
对于一个(u,v)点对,f[u]++,f[v]++,f[lca(u,v)]-=2,这样一来如果对i的子树的f求和,得到的值就是(i,fa[i])这条边被用了几次。
这样检验就能在O(n+m)完成。
lca我只会写树剖啊。
这数据是不是有点奇怪啊,我有一个点差点T了...(好把,其实应该是蒟蒻我太弱了~_~)
代码:
1 //2017.11.2 2 //tree 差分 二分 3 #include<iostream> 4 #include<cstdio> 5 #include<cstring> 6 using namespace std; 7 inline int read(); 8 int Max(int x,int y){return x>y?x:y;} 9 int ABS(int x){return x>0?x:-x;} 10 namespace lys{ 11 const int N = 3e5 + 7 ; 12 struct edge{ 13 int to; 14 int next; 15 int w; 16 }e[N*3]; 17 int sum[N],f[N],pre[N],fa[N],siz[N],dep[N],top[N],lca[N],len[N],u[N],v[N],dis[N],d[N],son[N]; 18 bool used[N]; 19 int n,m,cnt,M; 20 void add(int x,int y,int w){ 21 e[++cnt].to=y;e[cnt].next=pre[x];pre[x]=cnt;e[cnt].w=w; 22 e[++cnt].to=x;e[cnt].next=pre[y];pre[y]=cnt;e[cnt].w=w; 23 } 24 void dfs1(int node,int deep){ 25 dep[node]=deep; 26 siz[node]=1; 27 int i,v; 28 for(i=pre[node];~i;i=e[i].next){ 29 v=e[i].to; 30 if(v==fa[node]) continue ; 31 fa[v]=node; 32 d[v]=e[i].w; 33 dfs1(v,deep+1); 34 siz[node]+=siz[v]; 35 if(siz[son[node]]<siz[v]) son[node]=v; 36 } 37 } 38 void dfs2(int node,int tp,int ds){ 39 top[node]=tp; 40 dis[node]=ds+d[node]; 41 if(!son[node]) return ; 42 dfs2(son[node],tp,dis[node]); 43 int i,v; 44 for(i=pre[node];~i;i=e[i].next){ 45 v=e[i].to; 46 if(v==fa[node]||v==son[node]) continue ; 47 dfs2(v,v,0); 48 } 49 } 50 void LCA(int x,int y,int pos){ 51 int f1,f2; 52 while(true){ 53 f1=top[x],f2=top[y]; 54 if(f1==f2){ 55 if(dep[x]<dep[y]) lca[pos]=x; 56 else lca[pos]=y; 57 len[pos]+=ABS(dis[x]-dis[y]); 58 return ; 59 } 60 if(dep[f1]<dep[f2]){ 61 len[pos]+=dis[y]; 62 y=fa[f2]; 63 } 64 else{ 65 len[pos]+=dis[x]; 66 x=fa[f1]; 67 } 68 } 69 } 70 void dfs(int node){ 71 int i,v; 72 sum[node]=f[node]; 73 f[node]=0; 74 for(i=pre[node];~i;i=e[i].next){ 75 v=e[i].to; 76 if(v==fa[node]) continue ; 77 dfs(v); 78 sum[node]+=sum[v]; 79 } 80 } 81 bool chk(int mid){ 82 int num=0; 83 for(int i=1;i<=m;i++) if(len[i]>mid) num++,used[i]=true ; 84 for(int i=1;i<=m;i++) 85 if(used[i]) f[u[i]]++,f[v[i]]++,f[lca[i]]-=2,used[i]=false ; 86 dfs(1); 87 for(int i=1;i<=n;i++) if(sum[i]>=num&&d[i]>=(M-mid)) return true ; 88 return false ; 89 } 90 int main(){ 91 int i,x,y,w; 92 n=read(); m=read(); 93 memset(pre,-1,sizeof pre); 94 for(i=1;i<n;i++){ 95 x=read(); y=read(); w=read(); 96 add(x,y,w); 97 } 98 dfs1(1,1),dfs2(1,1,0); 99 for(i=1;i<=m;i++){ 100 u[i]=read(); v[i]=read(); 101 LCA(u[i],v[i],i); 102 M=Max(M,len[i]); 103 } 104 int l=0,r=M,mid; 105 while(l<r){ 106 mid=(l+r)>>1; 107 if(chk(mid)) r=mid; 108 else l=mid+1; 109 } 110 printf("%d ",l); 111 return 0; 112 } 113 } 114 int main(){ 115 lys::main(); 116 return 0; 117 } 118 inline int read(){ 119 int kk=0,ff=1; 120 char c=getchar(); 121 while(c<'0'||c>'9'){ 122 if(c=='-') ff=-1; 123 c=getchar(); 124 } 125 while(c>='0'&&c<='9') kk=kk*10+c-'0',c=getchar(); 126 return kk*ff; 127 }