入阵曲
题目描述
小 F 很喜欢数学,但是到了高中以后数学总是考不好。
有一天,他在数学课上发起了呆;他想起了过去的一年。一年前,当他初识算法竞赛的 时候,觉得整个世界都焕然一新。这世界上怎么会有这么多奇妙的东西?曾经自己觉得难以 解决的问题,被一个又一个算法轻松解决。
小 F 当时暗自觉得,与自己的幼稚相比起来,还有好多要学习的呢。
一年过去了,想想都还有点恍惚。
他至今还能记得,某天晚上听着入阵曲,激动地睡不着觉,写题写到鸡鸣时分都兴奋不 已。也许,这就是热血吧。
也就是在那个时候,小 F 学会了矩阵乘法。让两个矩阵乘几次就能算出斐波那契数列的 第 10100 项,真是奇妙无比呢。
不过,小 F 现在可不想手算矩阵乘法——他觉得好麻烦。取而代之的,是一个简单的小 问题。他写写画画,画出了一个 n×m 的矩阵,每个格子里都有一个不超过 kk 的正整数。
小 F 想问问你,这个矩阵里有多少个不同的子矩形中的数字之和是 kk 的倍数? 如果把一个子矩形用它的左上角和右下角描述为 (x1,y1,x2,y2),其中x1≤x2,y1≤y2; 那么,我们认为两个子矩形是不同的,当且仅当他们以 (x1,y1,x2,y2) 表示时不同;也就是 说,只要两个矩形以 (x1,y1,x2,y2) 表示时相同,就认为这两个矩形是同一个矩形,你应该 在你的答案里只算一次。
输入输出格式
输入格式:
从标准输入中读入数据。
输入第一行,包含三个正整数 n,m,k。
输入接下来 n 行,每行包含 m 个正整数,第 i 行第 j 列表示矩阵中第 i 行第 j 列 中所填的正整数 1ai,j。
输出格式:
输出到标准输出中。
输入一行一个非负整数,表示你的答案。
输入输出样例
输入样例1#:
2 3 2
1 2 1
2 1 2
输出样例1#:
6
说明
【样例 1 说明】
这些矩形是符合要求的: (1, 1, 1, 3),(1, 1, 2, 2),(1, 2, 1, 2),(1, 2, 2, 3),(2, 1, 2, 1),(2, 3, 2, 3)。
子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难,可以尝试只解 决一部分测试数据。
每个测试点的数据规模及特点如下表:(图来自luogu)
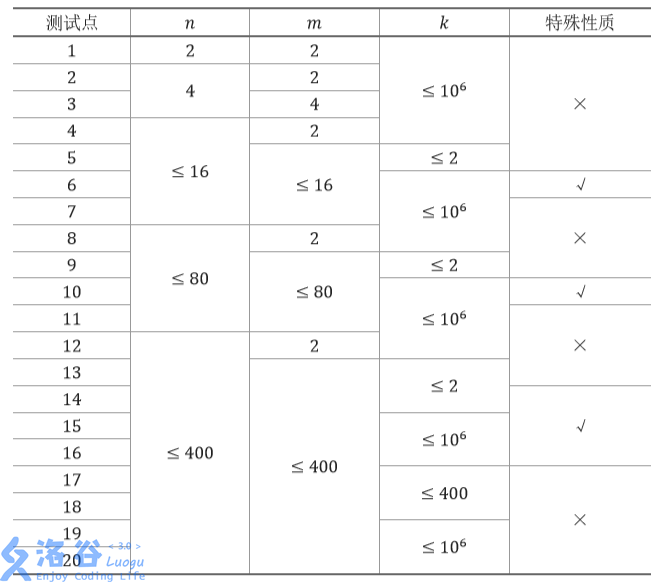
特殊性质:保证所有 ai,j 均相同。
处理前缀和,暴力枚举矩形,时间复杂度O(n4),得分:60。
注意到如果是一行的情况,记录r[m]表示前缀和mod k = m 的个数,贡献为:C2r[m],如果为m为0,还要再加上r[m]。
压行,枚举每一种列数,时间复杂度O(n3)。
代码:
1 //2017.11.2 2 //前缀和同余 3 #include<iostream> 4 #include<cstdio> 5 #include<cstring> 6 using namespace std; 7 typedef long long ll ; 8 inline int read(); 9 namespace lys{ 10 const int N = 4e2 + 7 ; 11 int a[N][N],r[1000007],find[N]; 12 bool used[N]; 13 int n,m,k; 14 ll ans; 15 int main(){ 16 int i,j,t,x,y,z; 17 n=read(); m=read(); k=read(); 18 for(i=1;i<=n;i++) 19 for(j=1;j<=m;j++){ 20 a[i][j]=read(),a[i][j]=(a[i][j]+a[i-1][j]+a[i][j-1]-a[i-1][j-1]+k)%k; 21 } 22 for(i=1;i<=n;i++){ 23 for(j=1;j+i-1<=n;j++){ 24 memset(used,false,sizeof used); 25 for(t=1;t<=m;t++){ 26 r[(a[j+i-1][t]-a[j-1][t]+k)%k]++; 27 find[t]=(a[j+i-1][t]-a[j-1][t]+k)%k; 28 } 29 for(t=1;t<=m;t++){ 30 if(used[t]) continue ; 31 if(!find[t]) ans+=r[find[t]]; 32 ans+=1LL*(r[find[t]]-1)*(r[find[t]])/2; 33 r[find[t]]=0; 34 used[t]=true ; 35 } 36 } 37 } 38 printf("%lld ",ans); 39 return 0; 40 } 41 } 42 int main(){ 43 lys::main(); 44 return 0; 45 } 46 inline int read(){ 47 int kk=0,ff=1; 48 char c=getchar(); 49 while(c<'0'||c>'9'){ 50 if(c=='-') ff=-1; 51 c=getchar(); 52 } 53 while(c>='0'&&c<='9') kk=kk*10+c-'0',c=getchar(); 54 return kk*ff; 55 }