斐波那契
题目描述
小 C 养了一些很可爱的兔子。 有一天,小 C 突然发现兔子们都是严格按照伟大的数学家斐波那契提出的模型来进行 繁衍:一对兔子从出生后第二个月起,每个月刚开始的时候都会产下一对小兔子。我们假定, 在整个过程中兔子不会出现任何意外。
小 C 把兔子按出生顺序,把兔子们从 1 开始标号,并且小 C 的兔子都是 1 号兔子和 1 号兔子的后代。如果某两对兔子是同时出生的,那么小 C 会将父母标号更小的一对优先标 号。
如果我们把这种关系用图画下来,前六个月大概就是这样的:
图来自luogu:

其中,一个箭头 A → B 表示 A 是 B 的祖先,相同的颜色表示同一个月出生的兔子。
为了更细致地了解兔子们是如何繁衍的,小 C 找来了一些兔子,并且向你提出了 m 个 问题:她想知道关于每两对兔子 a_iai和 b_ibi ,他们的最近公共祖先是谁。你能帮帮小 C 吗?
一对兔子的祖先是这对兔子以及他们父母(如果有的话)的祖先,而最近公共祖先是指 两对兔子所共有的祖先中,离他们的距离之和最近的一对兔子。比如,5 和 7 的最近公共祖 先是 2,1 和 2 的最近公共祖先是 1,6 和 6 的最近公共祖先是 6。
输入输出格式
输入格式:
从标准输入读入数据。 输入第一行,包含一个正整数 m。 输入接下来 m 行,每行包含 2 个正整数,表示 a_iai 和 b_ibi 。
输出格式:
输出到标准输出中。 输入一共 m 行,每行一个正整数,依次表示你对问题的答案。
输入输出样例
输入样例1#:
5
1 1
2 3
5 7
7 13
4 12
输出样例1#:
1
1
2
2
4
说明
【数据范围与约定】 子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难,可以尝试只解 决一部分测试数据。 每个测试点的数据规模及特点如下表:
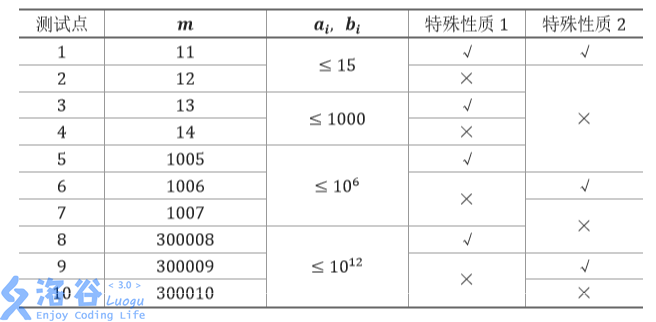
特殊性质 1:保证 ai,bi 均为某一个月出生的兔子中标号最大的一对兔子。例如,对 于前六个月,标号最大的兔子分别是 1, 2, 3, 5, 8, 13。
特殊性质 2:保证∣ai−bi∣≤1。
我一开始还以为是有什么公式可以算,真的是神经病。
发现每一个节点减去一个最大的斐波那契数就是其父亲节点,这有很多方法可以证明,比较严谨的是数学归纳法。
理解的话(找规律,证明只是求个安心,oi不需要证明),其实仔细想想就会发现第n个月的数量为f(n)=f(n-1)+f(n-2),每n+1月增加f(n+1)-f(n)=f(n-1)。
注意每次新增加的节点会在1那边开始加起,为f(n-1)+1,结束应该是下一个月连在1的开始也就应该是f(n)+1,而在这一个月是增加了f(n-1),而显然f(n-1)就是小于[f(n-1)+1,f(n)]的最大的斐波那契数。
那我们的命题就得证,虽说可能证的不严谨,但的确是这么一回事。
接下来还有比较坑爹的代码部分,我开始也发现了这个,但不晓得会有什么用,后来才知道就是很暴力的往上爬,爬到一样的就行了,真的是好朴素啊。
还有就是一个个爬还会TLE,要求真多,一个数不可能减去两个一样的斐波那契数,所以就一次减到完,能减就减。[蒟蒻打了二分查找结果TLE]
时间复杂度:O(60m)因为f60就超过10^12,真的是可恶。
代码:
1 //2017.11.2 2 //math 3 #include<iostream> 4 #include<cstdio> 5 #include<cstring> 6 using namespace std; 7 typedef long long ll ; 8 inline ll read(); 9 namespace lys{ 10 const ll inf = 1e12 ; 11 ll f[66]; 12 int m; 13 ll a,b; 14 void swap(ll &x,ll &y){int t=x;x=y;y=t;} 15 int main(){ 16 int i,l,r,mid; 17 scanf("%d",&m); 18 f[0]=1,f[1]=1; 19 for(i=2;i<=61;i++) f[i]=f[i-1]+f[i-2]; 20 while(m--){ 21 a=read(); b=read(); 22 for(i=60;i>=1;i--){ 23 if(a==b) break ; 24 if(a>f[i]) a-=f[i]; 25 if(b>f[i]) b-=f[i]; 26 } 27 printf("%lld ",a); 28 } 29 return 0; 30 } 31 } 32 int main(){ 33 lys::main(); 34 return 0; 35 } 36 inline ll read(){ 37 ll kk=0,ff=1; 38 char c=getchar(); 39 while(c<'0'||c>'9'){ 40 if(c=='-') ff=-1; 41 c=getchar(); 42 } 43 while(c>='0'&&c<='9') kk=kk*10+c-'0',c=getchar(); 44 return kk*ff; 45 }