感觉题质量挺好的,能学到东西或者完善技能树。
A了8题,实际上只有7题,有一题队友抬的,dp还是较弱项感觉。
这场感觉数学和思维偏重,开场签了A,B后就停滞了,挂机了一个多小时,还以为要2题结束了。
后来手推反倒是过了当时过的人还不多的E,信心又回来了,状态就上来啦。
顺序是ABEGDFCH,密集过题是1.5~3.5小时过了5题。前10分钟过了两题,(盲目)分析下似乎只要在线2个小时的高效状态就比较不错了。
记录一下思维。赛中没过的贴个代码。
按顺序来吧。
E.做计数
给的式子平方之后,就是要找sqrt(i*j)是整数的组合,记i*j=t 枚举sqrt(t),找t*t的因子即可。
话说我怎么看到这种多少对i,j,k就想到fft了。。。。。最近是不是做fft太多了。想了几分钟fft就排除了。。。
G.判正误
开场10分钟之后看到自闭的题,因为显然取模运算之后的数算出来的答案和原来不一样,也就是令人困惑的点。
但实际上仔细想想,YES的条件十分的苛刻,一旦YES,等式成立,那么这个等式按照任意质数模数算出来都应该同样是成立的。
所以对多个模数快速幂算一下即可,如果都成立,则YES,否则NO。
出题人卡了1e9+7,因为这个实在太常用了,似乎有随便换一个较大的质数就过的代码,实际上很不保险,知道你的模数,可以卡你的。
pow都可以过,有点晕。
D.数三角
看到题,n=500,算了下C(n,3)发现正好2e7左右,于是就开始写暴力,1s能过应该不是问题。。
写了暴力,就判钝角,然后忘了判共线,组不成三角形的情况,WA了一发就过了。
赛后补了n2log的做法,实际上n可以出到更大,建议参考HDU5784。
F.拿物品
交了5发错误的贪心策略,有先拿差值最大,先拿各自值最大等等策略的贪心。
最后冷静下来玩了临界情况的样例,当对方能得到很大的值,你是阻止对方拿?还是管自己拿大?然后就出来了,是拿a+b最大。
题解给的实际上非常有说服力。建议参考题解的证明。
C.算概率
开场自闭题2,最原始想法是组合数枚举嘛,就是你n个题做对k个,有C(n,k)的选法,但这样肯定做不了。
灵光乍现,或者参考群友提到的概率dp(虽然我没做过概率dp...)
想到dp,然后你就会了。
dp[i][j]记录 i 道题做对 j 道的概率。
然后转移很自然,就是 dp[i-1][j]*这道题做错 + dp[i-1][j-1]*这道题做对的概率。
二维dp的思路比较清晰。
然后实际上可以优化掉第二维。。。就是因为每次只与前一次有关,第二重循环反向枚举,滚动掉第二维?背包?(学了下,但还是不太会) 但复杂度n^2跑不了,数组开二维问题也不大。
(这就体现了dp弱项了....)
H.施魔法
就是排完序后 找 每段长度>=k的不重叠子段 使得总cost最小,cost为两个端点的差值。
队友抬的题,这题我比赛里也只会n^2的dp,
比赛时交了一发TLE的n^2的dp...实际上了就可以从式子上优化到O(n).
我是这么写的
for(int i=k;i<=n;++i)
{ for(int j=0;j<=i-k;++j) { dp[i]=min(dp[i],dp[j]+a[i]-a[j+1]); } }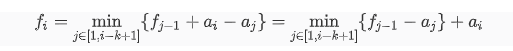
其实是跟题解里的式子一样的,第一个等号出来了,关键在于第二个等号,我们发现对于第二个循环枚举j来说,a[i]是多余的,可以提出来,然后剩下dp[j]-a[j+1]。
其实我们枚举第二个循环的目的就找这个最小的dp[j]-a[j+1],但这个式子只与当前的自变量有关,我们可以直接用一个pre变量在算的同时维护掉,省去这个第二重枚举。
就是dp递推转移式子的化简来实现dp复杂度的优化。
赛后给的题解里还是能学到挺多的感觉。
1 #include <bits/stdc++.h> 2 #ifndef ONLINE_JUDGE 3 #define debug(x) cout << #x << ": " << x << endl 4 #else 5 #define debug(x) 6 #endif 7 using namespace std; 8 typedef long long ll; 9 const int MAXN=3e5+7; 10 const int INF=0x3f3f3f3f; 11 const int MOD=1e9+7; 12 13 int dp[MAXN]; 14 int a[MAXN]; 15 16 int main() 17 { 18 ios::sync_with_stdio(false); 19 cin.tie(0); 20 int n,k; 21 cin>>n>>k; 22 for(int i=1;i<=n;++i) cin>>a[i]; 23 if(k==1) cout<<0<<endl; 24 else 25 { 26 memset(dp,0x3f,sizeof(dp)); 27 sort(a+1,a+n+1); 28 int pre=-a[1]; 29 for(int i=k;i<=n;++i) 30 { 31 dp[i]=pre+a[i]; 32 pre=min(pre,dp[i-k+1]-a[i-k+2]); 33 } 34 cout<<dp[n]<<endl; 35 } 36 return 0; 37 }
I.建通道
比赛里感觉思路大致方向对了,但没想好连边方式。导致想不好...
就是求个特殊位运算的最小生成树。
显然相同的v值之间无需建边,cost=0,就排序去重一下即可。剩下的点m个;
我们还需要在剩下m个点连m-1条边。注意此处的特判,别判n-1,而是去重后的点数-1。
然后找到最小的二进制位有0,有1,答案就是(m-1)*这位权值,为啥,因为所有的当前位这位二进制为1的点都可以和为0的这个点连,反之亦然。然后写了个O(30n)的写法。
出题人的写法统计二进位01存在性统计 用 & 和 | 扫一遍就更巧妙啦。学到了
1 #include <bits/stdc++.h> 2 #ifndef ONLINE_JUDGE 3 #define debug(x) cout << #x << ": " << x << endl 4 #else 5 #define debug(x) 6 #endif 7 using namespace std; 8 typedef long long ll; 9 const int MAXN=2e5+7; 10 const int INF=0x3f3f3f3f; 11 const int MOD=1e9+7; 12 13 int v[MAXN]; 14 15 int main() 16 { 17 ios::sync_with_stdio(false); 18 cin.tie(0); 19 int n; 20 cin>>n; 21 for(int i=0;i<n;++i)cin>>v[i]; 22 sort(v,v+n); 23 ll m=unique(v,v+n)-v; 24 if(m==1) cout<<0<<endl; 25 else 26 { 27 28 for(int i=0;i<=30;++i) 29 { 30 int cnt0=0,cnt1=0; 31 for(int j=0;j<m;++j) 32 { 33 if((v[j]&(1ll<<i))==0) cnt0++; 34 else cnt1++; 35 } 36 if(cnt0&&cnt1) 37 { 38 cout<<1ll*(1ll<<i)*(m-1)<<endl; 39 break; 40 } 41 } 42 } 43 return 0; 44 }
J.求函数
又是道可以学习的题。这种题之前还没遇到过。代入一下发现,就是 (((k(k(k(k*1+b)+b)+b)+b))) 这样的嵌套式子,拆开来就是题解给的那个式子。
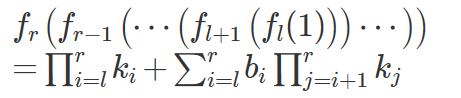
然后明确这个式子的区间合并方式,(这题的灵魂)就过了。
左边那个显然直接乘就好。
右边那个,.....好吧我讲不清,建议看题解,反正数学式子感觉到了就行...(逃~
https://ac.nowcoder.com/discuss/364961?type=101&order=0&pos=6&page=3
然后线段树分别维护这两个值就行,区间合并函数写好,或者重载一个运算符就行。
1 #include <bits/stdc++.h> 2 #ifndef ONLINE_JUDGE 3 #define debug(x) cout << #x << ": " << x << endl 4 #else 5 #define debug(x) 6 #endif 7 #define lson (o<<1) 8 #define rson (o<<1|1) 9 using namespace std; 10 typedef long long ll; 11 const int maxn=2e5+7; 12 const int INF=0x3f3f3f3f; 13 const int MOD=1e9+7; 14 15 struct node 16 { 17 ll k,b; 18 node(ll x=0,ll y=0):k(x),b(y){} 19 friend node operator + (const node &x,const node &y) 20 { 21 return {x.k*y.k%MOD,(x.b*y.k+y.b)%MOD}; 22 } 23 }t[maxn<<2]; 24 ll k[maxn],b[maxn]; 25 void build(int o,int l,int r) 26 { 27 if(l==r) 28 { 29 t[o]={k[l],b[l]}; 30 return ; 31 } 32 int mid=l+r>>1; 33 build(lson,l,mid); 34 build(rson,mid+1,r); 35 t[o]=t[lson]+t[rson]; 36 } 37 38 void update(int o,int l,int r,int pos,int k,int b) 39 { 40 if(l==r) 41 { 42 t[o]={k,b}; 43 return ; 44 } 45 int mid=l+r>>1; 46 if(pos<=mid) update(lson,l,mid,pos,k,b); 47 else update(rson,mid+1,r,pos,k,b); 48 t[o]=t[lson]+t[rson]; 49 } 50 node query(int o,int l,int r,int ql,int qr) 51 { 52 if(ql<=l && qr>=r) return t[o]; 53 int mid=l+r>>1; 54 if(qr<=mid) return query(lson,l,mid,ql,qr); 55 if(ql>mid) return query(rson,mid+1,r,ql,qr); 56 return query(lson,l,mid,ql,qr)+query(rson,mid+1,r,ql,qr); 57 } 58 59 int main() 60 { 61 int n,m; 62 scanf("%d%d",&n,&m); 63 for(int i=1;i<=n;++i) scanf("%lld",&k[i]); 64 for(int i=1;i<=n;++i) scanf("%lld",&b[i]); 65 build(1,1,n); 66 for(int i=0,op,l,r;i<m;++i) 67 { 68 scanf("%d",&op); 69 if(op==1) 70 { 71 int pos,x,y; 72 scanf("%d%d%d",&pos,&x,&y); 73 update(1,1,n,pos,x,y); 74 } 75 else 76 { 77 scanf("%d%d",&l,&r); 78 node res=query(1,1,n,l,r); 79 printf("%lld ",(res.k+res.b)%MOD); 80 } 81 } 82 return 0; 83 }
结束啦,逃...