简要赘述
良心出题人 (zhx) ,暴力的分给定十分充足,足足有 (200+) 题目也比较水。
预计得分 : (310)
实际得分 : (280)
(100 + 30 + 100 + 50)
(rank 5/83)
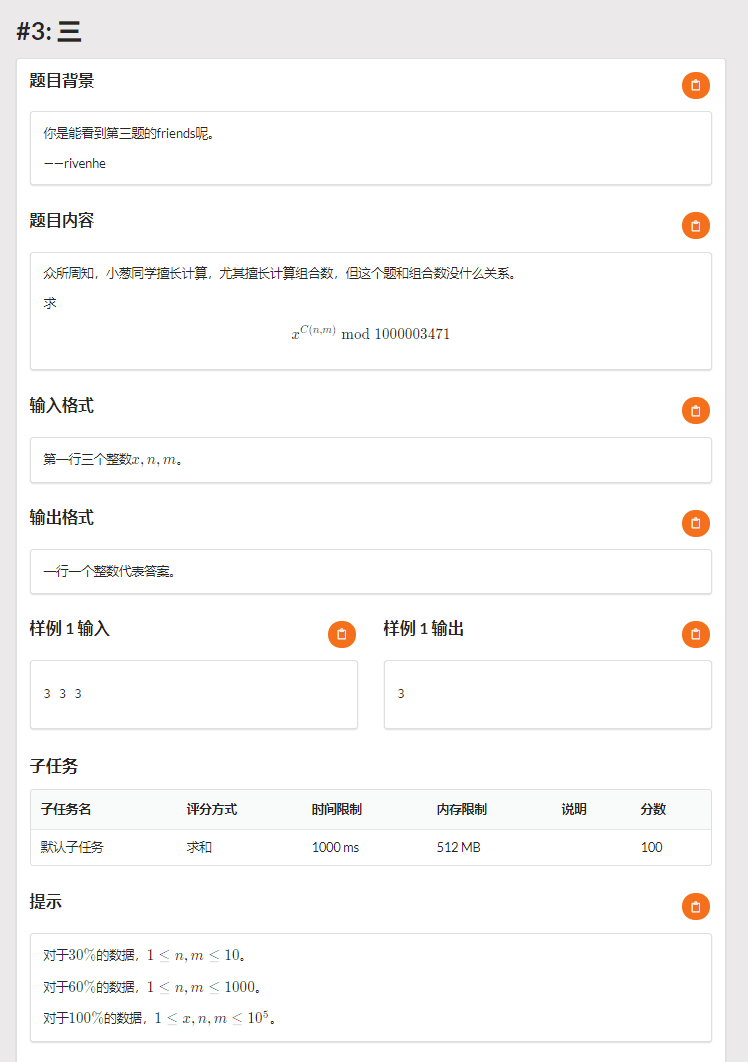
T1
高精度取膜
【(solution)】 : 直接类比读入取模,我们用字符串储存,然后直接 (*10) 取模即可
signed main() {
string s ; cin >> s ;
int y = read() , ret = 0;
for(qwq int i = 0 ; i < s.size() ; i++)
ret = (ret * 10 + (s[i] - '0')) % y ;
printf("%lld
" , ret) ;
return 0 ;
}
T2
用 (m) 种不同的 (1 imes 1) , (2 imes 2) 的两类方块 (这两类方块都有 (m) 种) 用这些正方形的块来覆盖 (2 imes n) 的长方形 。 (nleq 10^ 9)
【(solution)】 :
我们有显然的递推式 (f_i = m^3 imes (f_{i - 1} + 2 imes f_{i -2}))
signed main() {
n = read() , m = read() ;
f[0] = 1 ; f[1] = m * m * m ;
for(qwq int i = 2 ; i <= n ; i ++)
f[i] = f[i - 2] * 2 * m * m * m + f[i - 1] * m * m * m ;
printf("%lld
" , f[n]) ;
return 0 ;
}
我们发现 (n) 特别的大。并且我们发现 (f_i) 可以由 (f_{i-1}) 和 (f_{i-2}) 转移而来, 和斐波那契数列数列一样,我们考虑用矩阵加速。则就有
则我们就能够得到
当时在考试上写矩阵加速的我,傻逼的将初始化矩阵写翻了。
(Code)
/*
By : Zmonarch
知识点:
*/
#include <bits/stdc++.h>
#define int long long
#define qwq register
#define inf 2147483647
using namespace std ;
const int kmaxn = 1e6 + 10 ;
const int kmod = 1e9 + 7 ;
inline int read() {
int x = 0 , f = 1 ; char ch = getchar() ;
while(!isdigit(ch)) {if(ch == '-') f = - 1 ; ch = getchar() ;}
while( isdigit(ch)) {x = x * 10 + ch - '0' ; ch = getchar() ;}
return x * f ;
}
int n , m ;
int f[kmaxn] ;
struct Matrix {
int a[3][3] ;
Matrix() {memset(a , 0 , sizeof(a)) ;}
} ;
// f[i] = f[i - 2] * 2 * m ^3 + f[i - 1] * m ^ 3
Matrix operator ^ (const Matrix &m1 , const Matrix &m2)
{
Matrix m3 ; //m3.n = m1.n , m3.m = m2.m ;
for(qwq int i = 1 ; i <= 2 ; i++)
for(qwq int k = 1 ; k <= 2 ; k++)
for(qwq int j = 1 ; j <= 2 ; j++)
m3.a[i][j] = (m3.a[i][j] + m1.a[i][k] * m2.a[k][j]) % kmod ;
return m3 ;
}
Matrix quick(Matrix a , int b) {
Matrix ret ;
for(qwq int i = 1 ; i <= 2 ; i++) ret.a[i][i] = 1 ;
while(b)
{
if(b & 1) ret = ret ^ a;
a = a ^ a ;
b >>= 1 ;
}
return ret ;
}
signed main() {
n = read() , m = read() ;
Matrix base ; //base.m = base.n = 2 ;
base.a[1][1] = m % kmod * m % kmod * m % kmod ;
base.a[1][2] = 1 ;
base.a[2][1] = 2 * m % kmod * m % kmod * m % kmod;
base.a[2][2] = 0 ;
Matrix ans ;
ans.a[1][1] = m % kmod * m % kmod * m % kmod ; ans.a[1][2] = 1;
ans = ans ^ quick(base , n - 1) ;
printf("%lld
" , ans.a[1][1]) ;
return 0 ;
}
T3
求解 (x^{C_{n}^m} mod 1000003471)
哈哈哈,从 (szt) 那里嫖来的。
【(solution)】:
我们用 (mod = 1000003471) 写这个数太麻烦了,以 (mod) 代表一下。
我们发现 (mod) 是一个质数,我们就能知道我们可以用欧拉定理优化一波
(x^{C_{n}^{m} mod varphi(mod)})
(varphi(mod)) 我们发现这玩意不是个质数。
两种方法
- 1000003470 可以分解为 (2×3×5×53×677×929)
我们发现其实这个也就能将其搞一下 (a ext{%} 2 = 0 , a ext{%}5 = 0 dots a ext{%}929 = 0) 我们也就能够得到 (6) 个同余方程,我们用中国剩余定理莽上,就能够求解了。
std 干得
- 我们发现这是一个 (exlucas) 定理的板子,我们直接莽上。
我干得
/*
By : Zmonarch
知识点:欧拉定理,扩展卢卡斯定理
*/
#include <bits/stdc++.h>
#define int long long
#define qwq register
#define inf 2147483647
using namespace std ;
const int kmaxn = 1e6 + 10 ;
const int kmod = 1000003471 ;
inline int read() {
int x = 0 , f = 1 ; char ch = getchar() ;
while(!isdigit(ch)) {if(ch == '-') f = - 1 ; ch = getchar() ;}
while( isdigit(ch)) {x = x * 10 + ch - '0' ; ch = getchar() ;}
return x * f ;
}
int tot ;
int c[kmaxn] , d[kmaxn] , b[kmaxn];
/*int eular(int p) {
int phi = p ;
for(int i = 2 ; i <= sqrt(p) ; i++)
{
if(p % i == 0)
{
phi = phi / i * (i - 1) ;
while(p % i == 0) p /= i ;
}
}
if(p > 1) phi = phi / p * (p - 1) ;
return phi ;
}*/
inline int Qpow(int a,int b, qwq int mod) {
int ans = 1;
while (b) {
if (b & 1) ans = ans * a % mod;
a = a * a % mod;
b >>= 1;
}
return ans;
}
inline int ExGCD (int a, int b, int &x, int &y) {
if (!b) {x = 1, y = 0;return a ;}
int d = ExGCD (b, a % b, x, y);
int tmp = x;
x = y;
y = tmp - (a / b) * y;
return d;
}
inline int Inv (int a, int mod) {
int x = 0, y = 0;
ExGCD (a, mod, x, y);
return (x % mod + mod) % mod;
}
inline int Calc (int n, int p, int pk) {
if (n == 0) return 1;
int ans = 1;
for (qwq int i = 1; i <= pk; i ++)
if (i % p) ans = ans * i % pk;
ans = Qpow (ans, n / pk, pk);
for (qwq int i = 1; i <= n % pk; i ++)
if (i % p) ans = ans * i % pk;
return ans * Calc (n / p, p, pk) % pk;
}
inline int C (int n, int m, int p, int pk) {
if (n == 0 || m == 0 || n == m) return 1;
if (n < m) return 0;
int nn = Calc (n, p, pk), mm = Calc (m, p, pk), nm = Calc (n - m, p, pk), cnt = 0, k = n - m;
while (n) n /= p, cnt += n;
while (m) m /= p, cnt -= m;
while (k) k /= p, cnt -= k;
return nn * Inv (mm, pk) % pk * Inv (nm, pk) % pk * Qpow (p, cnt, pk) % pk;
}
inline int CRT () {
int M = 1, ans = 0;
for (qwq int i = 1; i <= tot; i ++) M *= c[i];
for (qwq int i = 1; i <= tot; i ++) d[i] = Inv (M / c[i], c[i]);
for (qwq int i = 1; i <= tot; i ++) ans += b[i] * (M / c[i]) * d[i];
return (ans % M + M) % M;
}
inline int ExLucas (int n, int m, int p) {
int tmp = sqrt (p);
for (qwq int i = 2; i <= tmp && p >= 1; i ++)
{
int pk = 1;
while (p % i == 0) p /= i, pk *= i;
if (pk > 1) b[++ tot] = C (n, m, i, pk), c[tot] = pk;
}
if (p > 1) b[++ tot] = C (n, m, p, p), c[tot] = p;
return CRT() ;
}
signed main() {
//int p = Eular(kmod) ; 我为什么还要筛一遍
int p = kmod - 1; //质数的话就是 varphi(n) = n - 1
int x = read() , n = read() , m = read() ;
int k = ExLucas(n , m , p) ; // C(n ,m) % p
//printf("%lld
" ,k) ;
int ret = Qpow(x , k , kmod) ;
printf("%lld" , ret) ;
return 0 ;
}
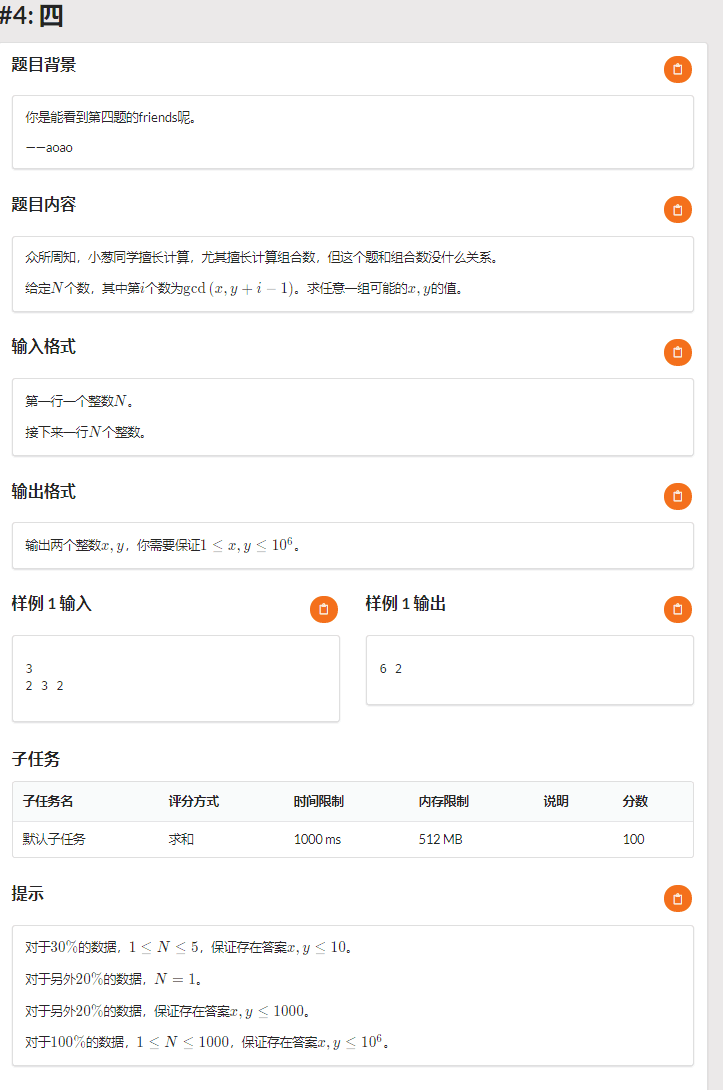
T4
给定 (n) 个数 (a_i),求解使得 (a_i = gcd(x , y + i - 1)) 成立的任意 (x,y) 、
【(solution)】 ;
- 暴力 : 我们可以直接枚举 (x,y) 看一下是否能够成立 , 你能得到 (30) 分。
我们特判一下 (n = 1) 的时候,直接输出那个数,我们能得到 (20) 分。
int gcd(int a , int b){ return !b ? a : gcd(b , a % b) ;}
signed main() {
int n = read() ;
if(n == 1) { int num = read() ; printf("%lld %lld" , num , num) ; ; return 0 ; }
for(qwq int i = 1 ; i <= n ; i++) a[i] = read() ;
for(qwq int i = 1 ; i <= n ; i++)
{
for(qwq int x = 1 ; x <= 10 ; x++)
{
for(qwq int y = 1 ; y <= 10 ; y++)
{
if(a[i] == gcd(x , y + i - 1))
{
printf("%lld %lld" , x , y) ;
return 0 ;
}
}
}
}
return 0 ;
}
- 正解:我们可以显然的看出 (x = lcm_{i = 1}^{n} a_i) 的,但是 (y) 显然不是那么乐观,我们搞搞化简,我们发现这么个玩意
我们发现这玩意是个 (excrt) , 模板莽上。
这里选择用大数翻倍法 : (1.) 好写, (2.) 没写过,练一下。
/*
By : Zmonarch
知识点:
*/
#include <bits/stdc++.h>
#define int long long
#define qwq register
#define inf 2147483647
using namespace std ;
const int kmaxn = 1e6 + 10 ;
const int kmod = 98244353 ;
inline int read() {
int x = 0 , f = 1 ; char ch = getchar() ;
while(!isdigit(ch)) {if(ch == '-') f = - 1 ; ch = getchar() ;}
while( isdigit(ch)) {x = x * 10 + ch - '0' ; ch = getchar() ;}
return x * f ;
}
int a[kmaxn] ;
int gcd(int a , int b){ return !b ? a : gcd(b , a % b) ;}
void merge(int &n1 , int &m1 , int n2 , int m2) {
if(m1 < m2) swap(m1 , m2) , swap(m1 , m2) ;
while(n1 % m2 != n2) n1 += m1 ;
m1 = m1 / gcd(m1 , m2) * m2 ;
}
signed main() {
int n = read() ;
for(qwq int i = 1 ; i <= n ; i++) a[i] = read() ;
int x = 1 ;
for(qwq int i = 1 ; i <= n ; i++)
x = x / gcd(x , a[i]) * a[i] ;
int n1 = 0 , m1 = 1 ;
for(qwq int i = 1 ; i <= n ; i++)
{
int n2 = ((1 - i) % a[i] + a[i]) % a[i] ;
int m2 = a[i] ;
merge(n1 , m1 , n2 , m2) ;
}
printf("%lld %lld
" , x , n1) ;
return 0 ;
}
Std
钟神的代码确定不要一下吗?
(T1)
#include<cstdio>
#include<cstdlib>
#include<cstring>
using namespace std;
int m;
char s[100010];
int main()
{
scanf("%s",s+1);
scanf("%d",&m);
int l=strlen(s+1);
long long ans=0;
for (int a=1;a<=l;a++)
ans=(ans*10+s[a]-'0')%m;
printf("%lld
",ans);
return 0;
}
(T2)
#include<cstdio>
#include<cstdlib>
#include<cstring>
using namespace std;
const int mo=1000000007;
int n,m;
struct matrix
{
int z[2][2];
matrix()
{
memset(z,0,sizeof(z));
}
}m1,m2;
matrix operator*(const matrix &m1,const matrix &m2)
{
matrix m3;
for (int a=0;a<2;a++)
for (int b=0;b<2;b++)
for (int c=0;c<2;c++)
m3.z[a][c] =(m3.z[a][c]+1ll*m1.z[a][b]*m2.z[b][c])%mo;
return m3;
}
int main()
{
scanf("%d%d",&n,&m);
if (n==1) printf("%lld
",1ll*m*m%mo*m%mo);
else
{
m1.z[0][0]=1;
m1.z[0][1]=1ll*m*m%mo*m%mo;
m2.z[0][0]=0;m2.z[1][0]=1;
m2.z[0][1]=2ll*m*m%mo*m%mo;
m2.z[1][1]=1ll*m*m%mo*m%mo;
while (n)
{
if (n&1) m1=m1*m2;
m2=m2*m2;
n>>=1;
}
printf("%d
",m1.z[0][0]);
}
return 0;
}
(T3)
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
const int mo=1000003471;
int pcnt,plist[10];
int x,n,m,C[1000][1000];
int gcd(int a,int b)
{
if (!b) return a;
else return gcd(b,a%b);
}
int pow(int a,int b,int mo)
{
int ans=1;
while (b)
{
if (b&1) ans=1ll*ans*a%mo;
a=1ll*a*a%mo;
b>>=1;
}
return ans;
}
int get(int n,int m,int p)
{
C[0][0]=1;
for (int a=1;a<p;a++)
{
C[a][0]=1;
for (int b=1;b<=a;b++)
{
C[a][b]=C[a-1][b-1]+C[a-1][b];
if (C[a][b]>=p) C[a][b]-=p;
}
}
int ans=1;
while (n!=0 || m!=0)
{
ans=1ll*ans*C[n%p][m%p]%p;
n/=p;
m/=p;
}
return ans;
}
void merge(int &v1,int &m1,int v2,int m2)
{
if (m1<m2) swap(v1,v2),swap(m1,m2);
while (v1%m2!=v2)
v1+=m1;
m1=m1/gcd(m1,m2)*m2;
}
int work(int n,int m)
{
int v1=0,n1=1;
for (int a=1;a<=pcnt;a++)
{
int v2=get(n,m,plist[a]),n2=plist[a];
merge(v1,n1,v2,n2);
}
return v1;
}
int main()
{
int v=mo-1;
for (int a=2;a<=v;a++)
if (v%a==0)
{
plist[++pcnt]=a;
while (v%a==0)
v/=a;
}
scanf("%d%d%d",&x,&n,&m);
printf("%d
",pow(x,work(n,m),mo));
return 0;
}
(T4)
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<algorithm>
using namespace std;
int n,z[1010];
int gcd(int a,int b)
{
if (!b) return a;
else return gcd(b,a%b);
}
void merge(int &v1,int &m1,int v2,int m2)
{
if (m1<m2) swap(v1,v2),swap(m1,m2);
while (v1%m2!=v2)
v1+=m1;
m1=m1/gcd(m1,m2)*m2;
}
int main()
{
scanf("%d",&n);
for (int a=1;a<=n;a++)
scanf("%d",&z[a]);
int x=1;
for (int a=1;a<=n;a++)
x=x/gcd(x,z[a])*z[a];
int v1=0,m1=1;
for (int a=1;a<=n;a++)
{
int v2=((1-a)%z[a]+z[a])%z[a];
int m2=z[a];
merge(v1,m1,v2,m2);
}
printf("%d %d
",x,v1);
return 0;
}