递归(Recursive):
递归是一种算法,在函数中调用自身的算法称为递归。它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解。
用递归法解决问题的特点
- 一个问题可以被分解成多个小问题,求解小问题后即可得到大问题的解。
- 大问题与分解后的小问题,除了数据规模不同,求解思路完全一样。
- 存在明确的递归终止条件。
递归三要素
- 函数定义(这个函数的功能是什么)
- 递归终止条件
- 函数等价关系式:只需关注如何将从大问题转换小问题,不用关注小问题怎样得到解(假设小问题已经得到解)
递归例题
1. 斐波那契数列
斐波那契数列的是这样一个数列:1、1、2、3、5、8、13、21、34....,即第一项 f(1) = 1,第二项 f(2) = 1.....,第 n 项目为 f(n) = f(n-1) + f(n-2)。求第 n 项的值是多少。
- 函数定义:
假设fib(n) 是求解第n项的值,即得到:
int fib(int n){
}
- 递归终止条件
当n = 1 或 n = 2时,f(1) = f(2) = 1。递归结束条件即为 n <= 2,
int fib(int n){
if(n <= 2)
return 1;
}
- 函数关系式:
斐波那契数列的递推式为f(n) = f(n-1) + f(n-2),
int fib(int n){
if(n <= 2)
return 1;
return f(n-1) + f(n-2);
}
2. 归并排序
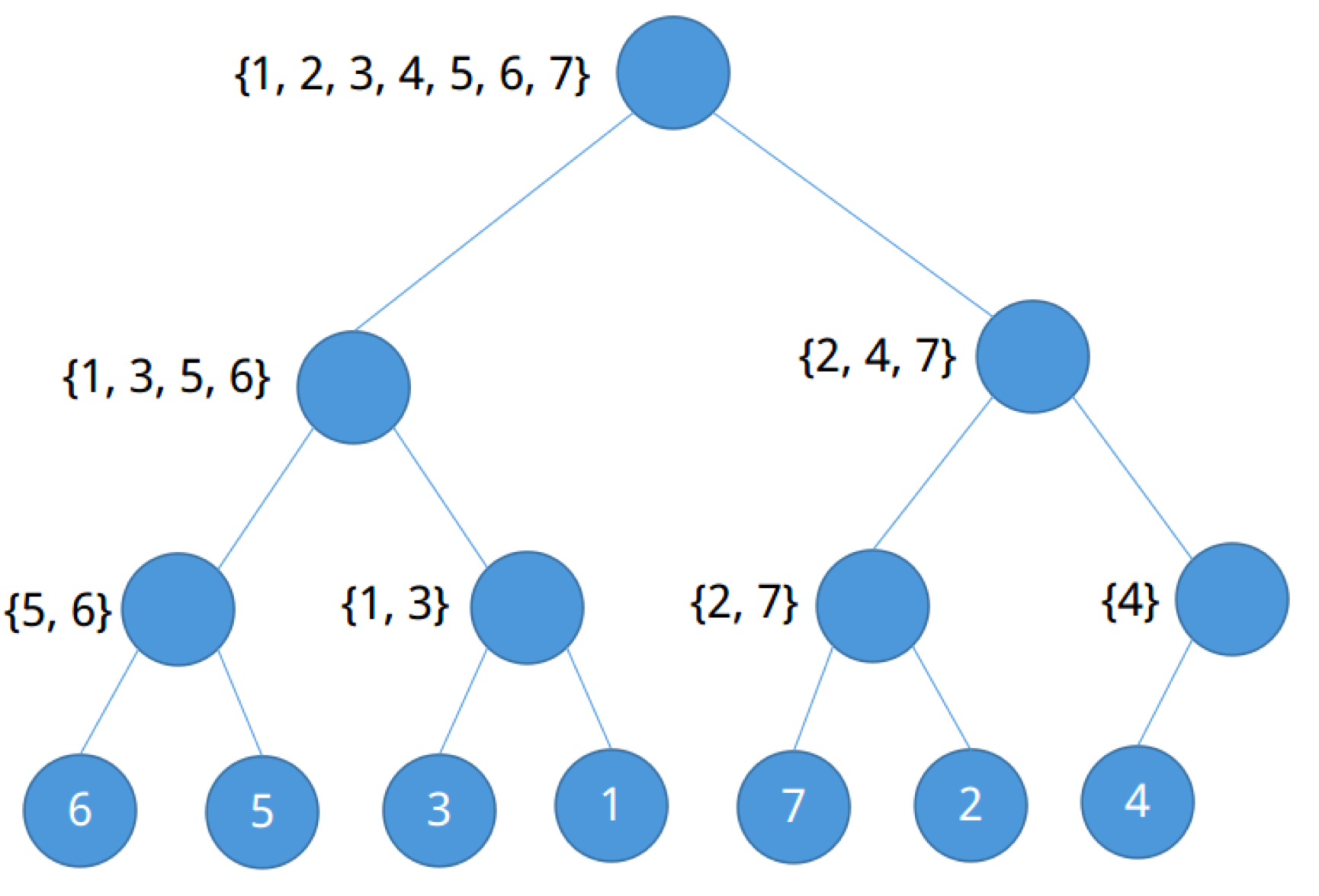
使用归并排序,排列{6,5,3,1,7,2,4}。
如上图所示,为了对整个序列进行排序,不断的将原始序列划分为最小序列,当为子序列长度为1时不可再分,此时即为递归终止条件。
为了得到一个有序序列,需要再将最小序列逐个合并得到最后答案。
#include<iostream>
#include<vector>
#include "merge_sort.h"
using namespace std;
void merge_sort(int left, int right, vector<int> &arr)
{
//递归终止条件
if (left >= right)
return;
int mid = (right + left)/ 2;
merge_sort(left, mid, arr);
merge_sort(mid + 1, right, arr);
merge(left, mid, right, arr);
}
//两两归并
void merge(int left, int mid, int right, vector<int> &arr)
{
vector<int> temp(arr.size());
int i = left; //左序列指针
int j = mid + 1; //右序列指针
int index = 0;//临时指针
while (i <= mid && j <= right)
{
if (arr[i] <= arr[j])
temp[index++] = arr[i++];
else
temp[index++] = arr[j++];
}
while (i <= mid) {//将左边剩余元素填充进temp中
temp[index++] = arr[i++];
}
while (j <= right) {//将右序列剩余元素填充进temp中
temp[index++] = arr[j++];
}
//将temp中的元素全部拷贝到原数组中
index = 0;
while (left <= right) {
cout <<left << endl;
arr[left++] = temp[index++];
}
}
int main()
{
vector<int> arr = { 8, 6,2,3,1,5,7,4};
merge_sort(0, arr.size()-1, arr);
for (int i = 0; i < arr.size(); i++)
{
cout << arr[i] << ' ';
}
cout << endl;
system("pause");
return 0;
}