2021.1.26 学习KMP算法

学习视频：https://www.bilibili.com/video/BV1Px411z7Yo/?spm_id_from=333.788.videocard.10
文本摘录：https://www.zhihu.com/question/21923021/answer/1032665486

KMP算法是一种字符串匹配算法，可以在 O(n+m) 的时间复杂度内实现两个字符串的匹配。
字符串匹配问题：字符串 P 是否为字符串 S 的子串？如果是，它出现在 S 的哪些位置？” 其中 S 称为主串；P 称为模式串。

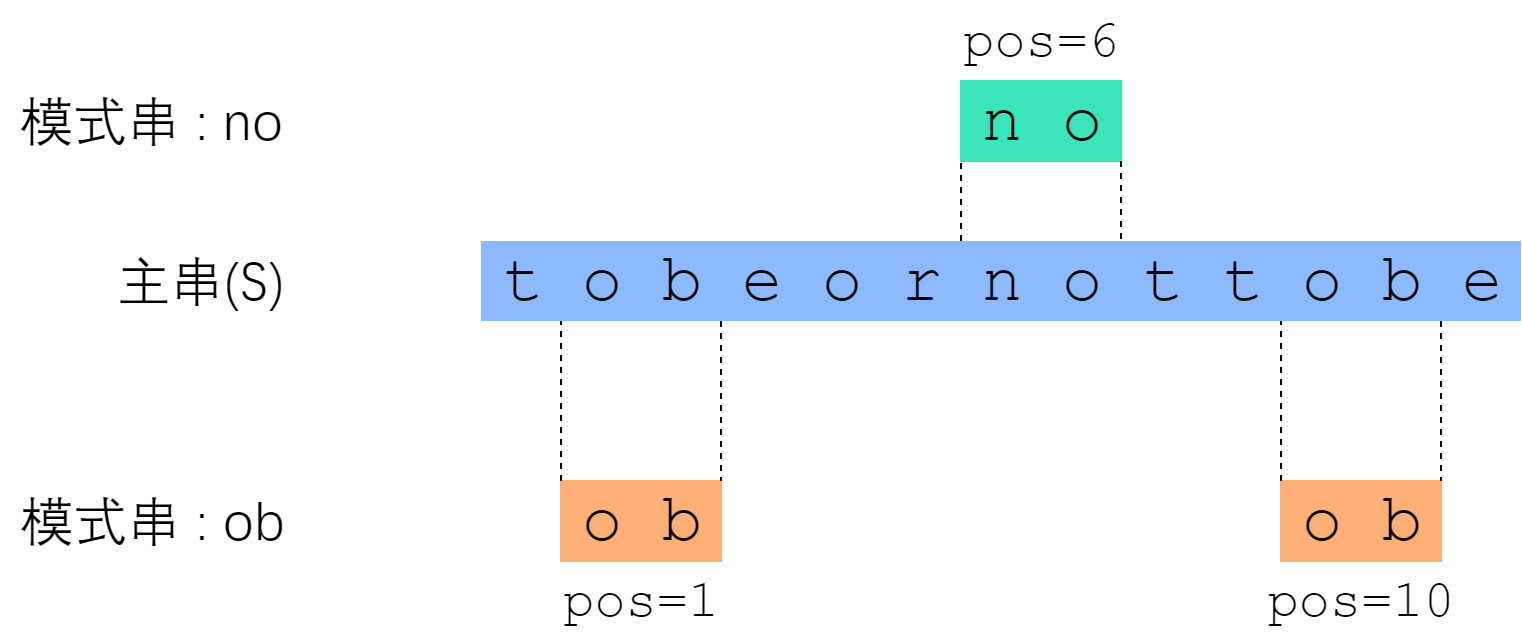
1. 朴素算法-Brute-Force
   最朴素的方式即是从前往后逐字符比较，一旦遇到不相同的字符，就返回False；如果两个字符串都结束了，仍然没有出现不对应的字符，则返回True。
   示意图如下：
   
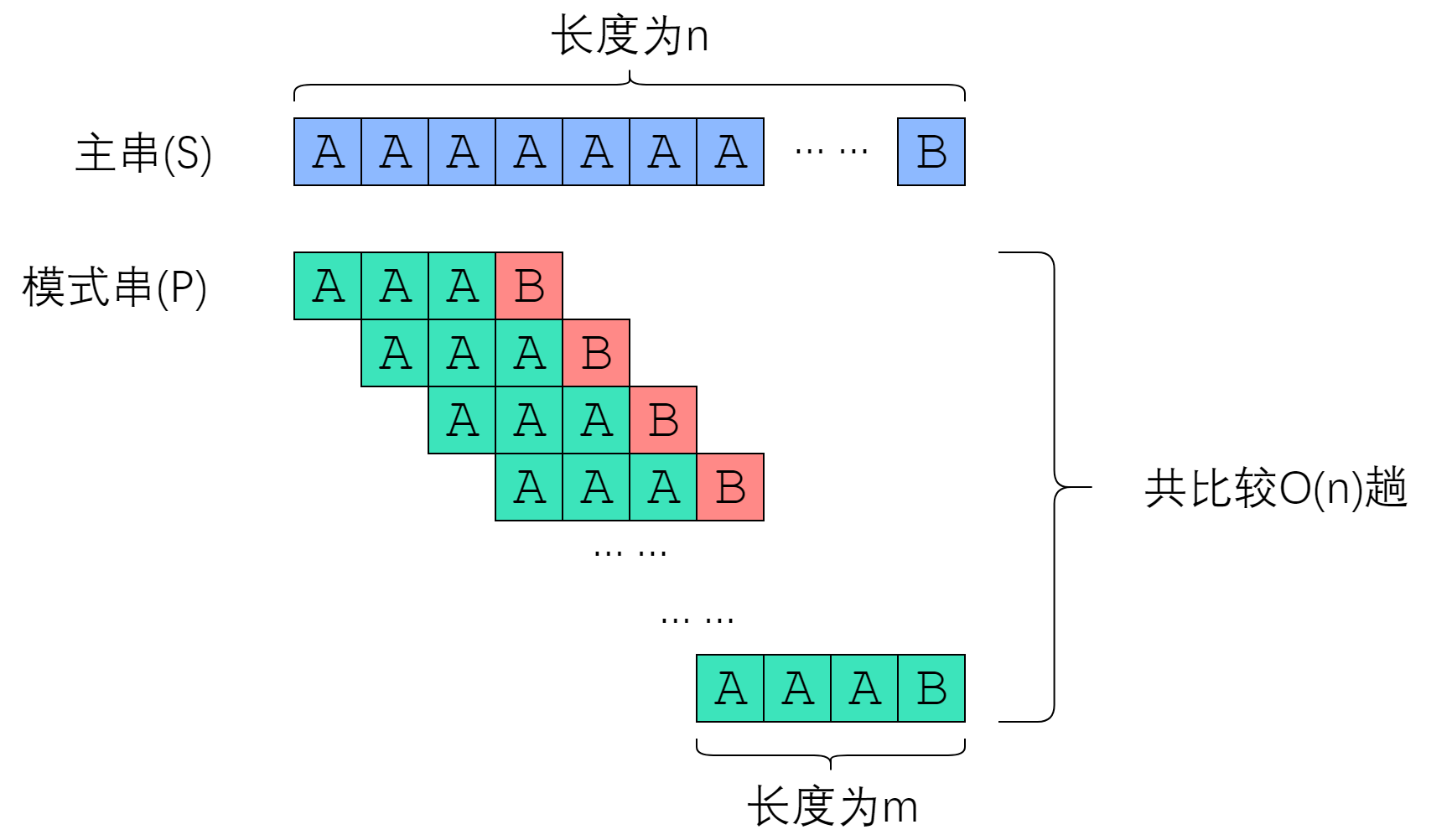
   这种方式的时间复杂度为O(nm),效率非常低。
   在 Brute-Force 中，如果从 S[i] 开始的那一趟比较失败了，算法会直接开始尝试从 S[i+1] 开始比较。这种行为，属于典型的“没有从之前的错误中学到东西”。我们应当注意到，一次失败的匹配，会给我们提供宝贵的信息——如果 S[i : i+len(P)] 与 P 的匹配是在第 r 个位置失败的，那么从 S[i] 开始的 (r-1) 个连续字符，一定与 P 的前 (r-1) 个字符一模一样！即可得主串的某一个子串等于模式串的某一个前缀。
   
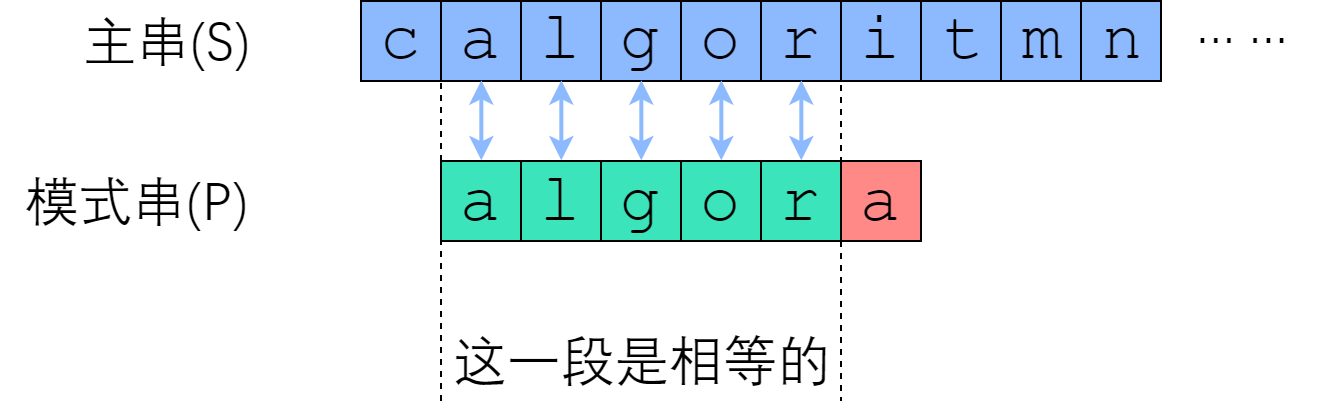
   2.KMP算法
   跳过一些不可能匹配成功的字符串比较，尽量减少比较的趟数。
   假设在匹配过程中，P[0] 到 P[i] 这一段子串中，前k个字符与后k个字符一模一样。如果在 P[r]失配, 那我们可以拿前k个字符顶替后K个字符的位置，让匹配继续下去！示意图如下：
   
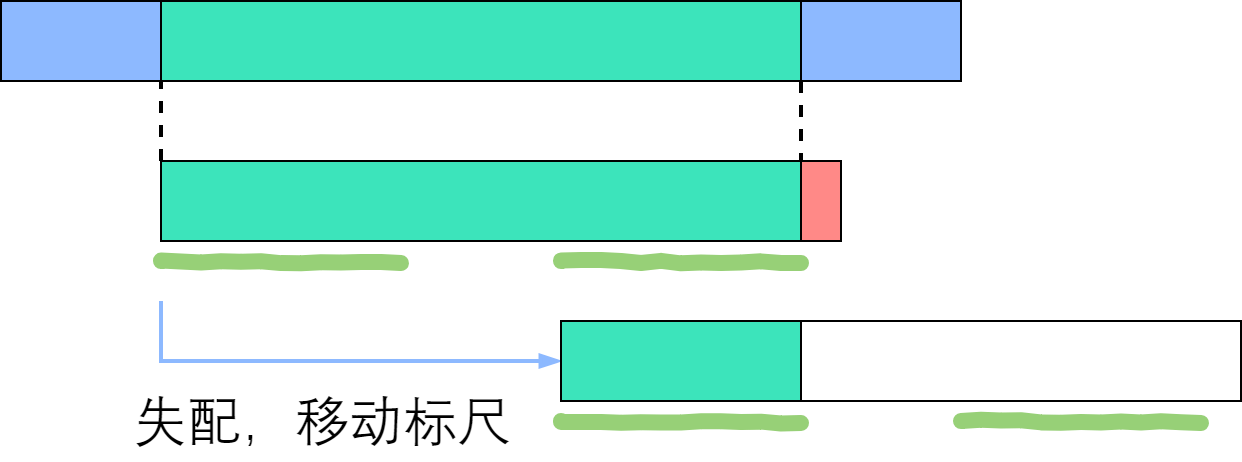
   由此可以看出绿色部分是控制模式串移动的关键-最长公共前后缀。
2. 最长公共前后缀
   前缀：包含首字母不包含尾字母的子串
   后缀：包含尾字母不包含首字母的字串
   例子：ababa
   前缀集：{”a”, ”ab”, ”aba”, ”abab”}
   后缀集：{”baba”, ”aba”, ”ba”, ”a”}
   公共前后缀集：{”a”, ”aba”}，其中最长的元素为”aba”，长度为3。
   基于上述知识，可以试图来理解KMP的核心部分-PMT（部分匹配表），PMT中的值是字符串的前缀集合与后缀集合的交集中最长元素的长度。
   为了编程的方便， 一般不直接使用PMT数组，而是将PMT数组向后偏移一位。我们把新得到的这个数组称为next数组。在把PMT进行向右偏移时，第0位的值，我们将其设成了-1，这只是为了编程的方便，并没有其他的意义。
   例如：abababca字符串的PMT和next
   

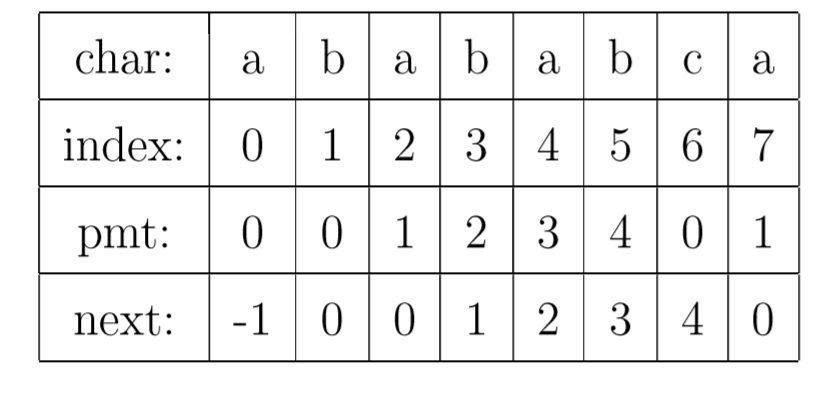
现在，我们看一下如何编程快速求得next数组。其实，求next数组的过程完全可以看成字符串匹配的过程，即以模式字符串为主字符串，以模式字符串的前缀为目标字符串，一旦字符串匹配成功，那么当前的next值就是匹配成功的字符串的长度。（注意next数组是pmt数组右移一位后的结果）
求最长公共前缀pmt数组：

pmt数组右移一位得next数组：

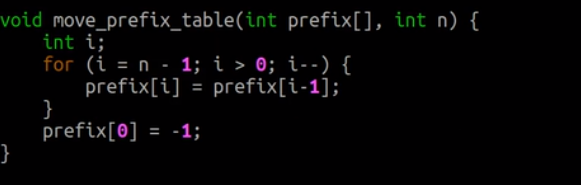
由此可以得出KMP算法：