lower_bound && upper_bound

 用lower_bound进行二分查找

●在从小到大排好序的基本类型数组上进行二分查找。

　　这是二分查找的一种版本，试图在已排序的[first,last)中寻找元素value。如果[first,last)具有与value相等的元素（s），便返回一个迭代器，指向其中第一个元素。如果没有这样的元素存在，便返回“假设这样的元素存在是应该出现的位置”。也就是说，它会返回一个迭代器，指向第一个“不小于value的元素”。如果value大于[first,last)内的任何一个元素，则返回last。以稍许不同的观点来看lower_bound，其返回值是“在不破坏顺序状态的原则下，可插入value的第一个位置”。如下图

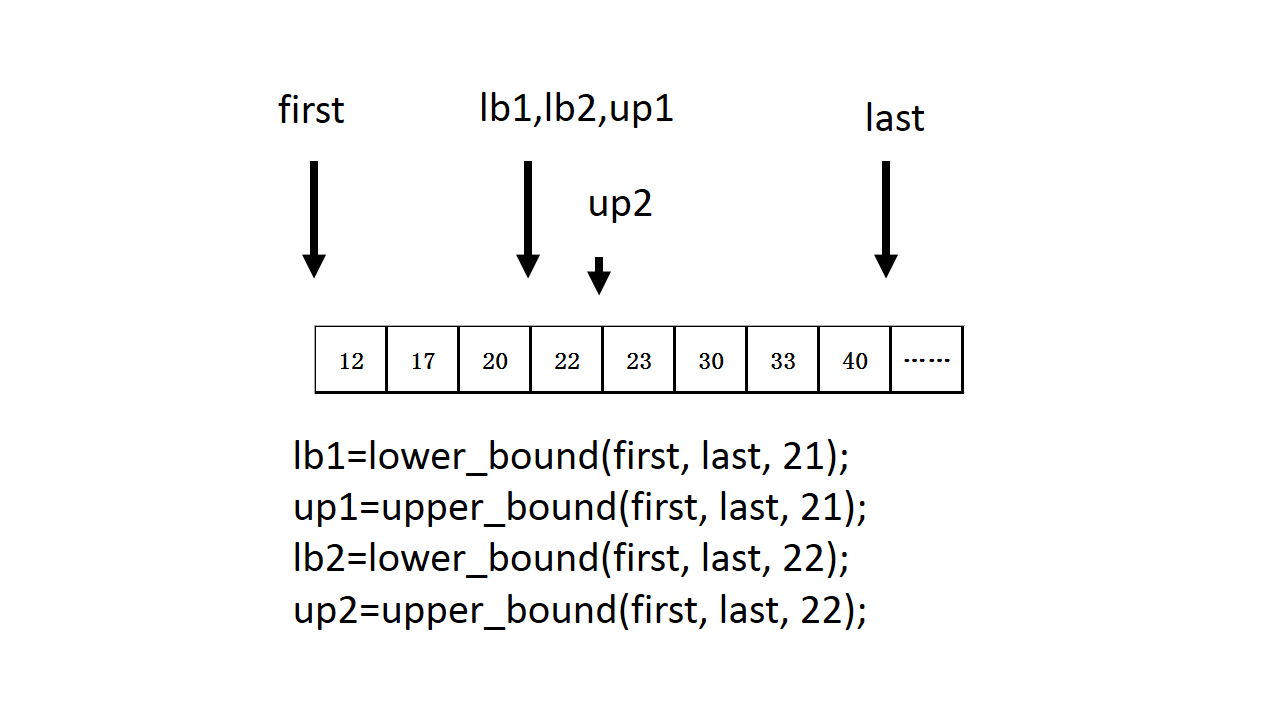
　　具体的用法是：

　　I

　　在对元素类型为T的从小到大排好序的基本类型的数组中进行查找。

　　 T * lower_bound ( 数组名 + n1, 数组名 + n2 , 值 );

　　* p 是查找区间里下标最小的，大于等于“值”的元素。如果找不到，p指向下标为n2的元素。

　　II

　　在元素为任意的T类型、按照自定义排序规则排好序的数组中进行查找。

　　T * lower_bound ( 数组名 + n1, 数组名 + n2, 值 , 排序规则结构名());

　　返回一个指针 T * P；

　　* P是查找区间里下标最小的，按自定义排序规则，可以排在“值”后面的元素。如果找不到，p指向下标为n2的元素。

　　这个算法有两个版本，版本1采用operator<进行比较，版本2采用仿函数comp。更正式地说，版本1返回[first,last)中最远的迭代器i，使得[first,i)中的每个迭代器j都满足 *j < value。版本2返回[first,last)中最远的迭代器i，使[first,i)中的每个迭代器j都满足“comp(j *, value)为真”。

　　函数原型就不给了，讲一讲用法就行了。

用upper_bound进行二分查找

　　算法upper_bound是二分查找（binary_search）的另一个版本。它试图在已排序的[first,last)中寻找value。更明确地说，它会返回 “在不破坏顺序的情况下，可插入 value的最后一个合适的位置”。

　　　由于STL规范“区间圈定”时的起头和结尾并不对称（是的，[first,last)包含first但不包含last），所以 upper_bound 与lower_bound 的返回值意义大有不同。如果你查找某值，而它的确出现在区间内，则 lower_bound 返回的是一个指向该元素的迭代器。然而upper_bound 不这么做。因为upper_bound所返回的是在不破坏排序状态的情况下，value 可被插入的“最后一个”合适的位置。如果value存在，那么它返回的迭代器将指向value的下一位置，而非指向value本身。

　　upper_bound有两个版本，版本一采用operator < 进行比较，版本二采用仿函数comp。更正式地说，版本一返回[first，last） 区间内最远的迭代器i，使[first,i)内的每一个迭代器j都满足 "value < *j"不为真。版本二返回[first,last)区间内最远的迭代器i，使[first,last)中的每个迭代器j都满足"comp( value , *j )不为真"。

　　下面是upper_bound的具体用法：

　　I

　　在元素类型为T的从小到大排好序的基本类型的数组中进行查找：

　　T * upper_bound ( 数组名 + n1, 数组名 + n2, 值)；

　　返回一个指针 T * p；

　　*p 是查找区间里下标最小的、大于“值”的元素。如果找不到，p指向下标为n2的元素。

　　II

　　在元素为任意的T类型、按照自定义排序规则排好序的数组中进行查找

　　T * upper_bound( 数组名 + n1, 数组名 + n2  ,  值 ,排序规则结构名());

　　返回一个指针 T * p；

　　* p是查找区间里下标最小的，按自定义排序规则，必须排在“值”后面的元素。如果找不到，p指向下标为n2的元素。

lower_bound&upper_bound用法实例

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
struct rule
{
    bool operator() ( const int & a1, const int & a2)
    {
        return a1%10 < a2%10;// 按照个位数由小到大排序 
    }
};
void print(int a[],int size)
{
    for(int i = 0;i < size;i ++)
        cout << a[i] << ",";
    cout << endl;
}
#define NUM 7
int main()
{
    int a[NUM] = { 12,5,3,5,98,21,7};
    sort(a,a+NUM);
    print(a,NUM);// =>3,5,5,7,12,21,98,
    
    int * p = lower_bound( a, a + NUM, 5);
    cout << *p << "," << p-a << endl; //=>5,1
    
    p = upper_bound ( a, a + NUM, 5);
    cout << *p << endl;//=>7
    cout << * upper_bound ( a, a+NUM, 13)<< endl;//=>21
    
    sort( a, a + NUM, rule()); 
    print( a, NUM);//=>21,12,3,5,5,7,98,
    
    cout << * lower_bound ( a, a + NUM , 16, rule()) << endl;//=>7
    
    cout << lower_bound ( a, a + NUM , 25, rule()) - a <<endl;//=>3
    
    cout << upper_bound ( a, a + NUM, 18, rule()) - a <<endl;//=>7

    if ( upper_bound ( a , a + NUM , 18 , rule()) == a + NUM)
        cout << "NOT FOUND" << endl; //=>not found

    cout << * upper_bound ( a, a + NUM, 5 , rule()) << endl;//=>7

    cout << * upper_bound ( a, a + NUM, 4 , rule()) << endl;//=>5
    return 0;
}