Educational Codeforces Round 125 (Rated for Div. 2) E. Star MST

折磨了我三天的\(DP\)，终于看懂啦。
首先，如果想要有题目要求的效果，那么最短的边一定都是与\(1\)相连的，就是一个菊花图，生成树里的边就是最短的边。

\(f[i][j]\)表示已经有\(i\)个点与\(1\)相连，且最大权值不超过\(j\)的方案。

那么我们考虑如何从\(j\)转移到\(j + 1\)，看下图，已经连接了\(i\)个点，且最大值不超过\(j\)。

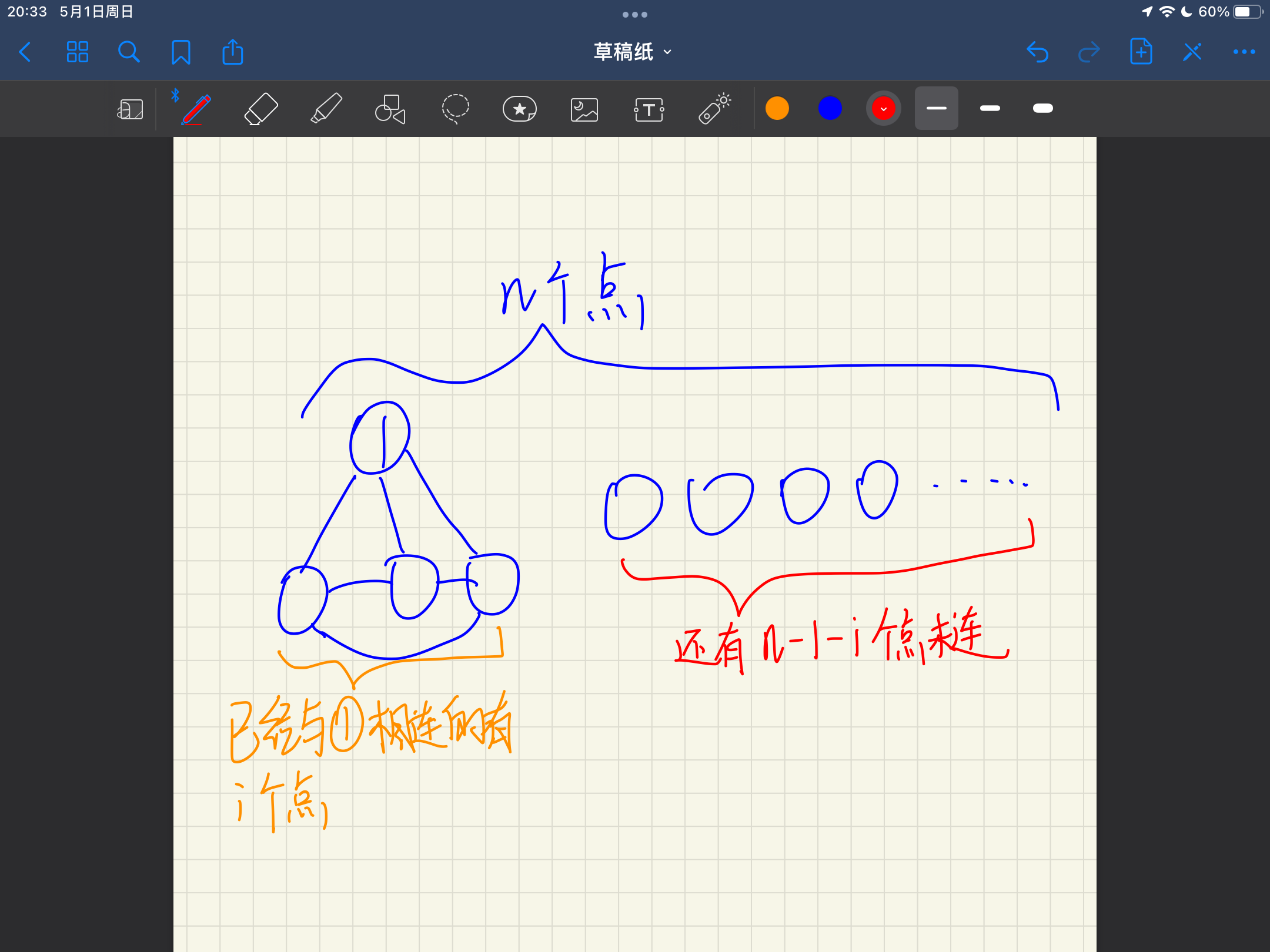
那么我们从右边\(n-1-i\)个点中选\(t\)个点\(1\)号点相连，令它们的边权是\(j + 1\)，那么也就是说现在有\(i + t\)个点的与\(1\)相连的那条边权已经确定了，这就是我们的\(f[i + t][j + 1]\)的状态。

那么对于现在已经选定的这\(i + t\)个点，右边t个点内部只要边权满足\([j + 1, k]\)就可以随便连，然后\(i\)个点与\(t\)个点之间同样只要满足\([j + 1, k]\)就可以随便连。

(为了图的美观，左边\(i\)个点与右边\(t\)个点先不画边了)

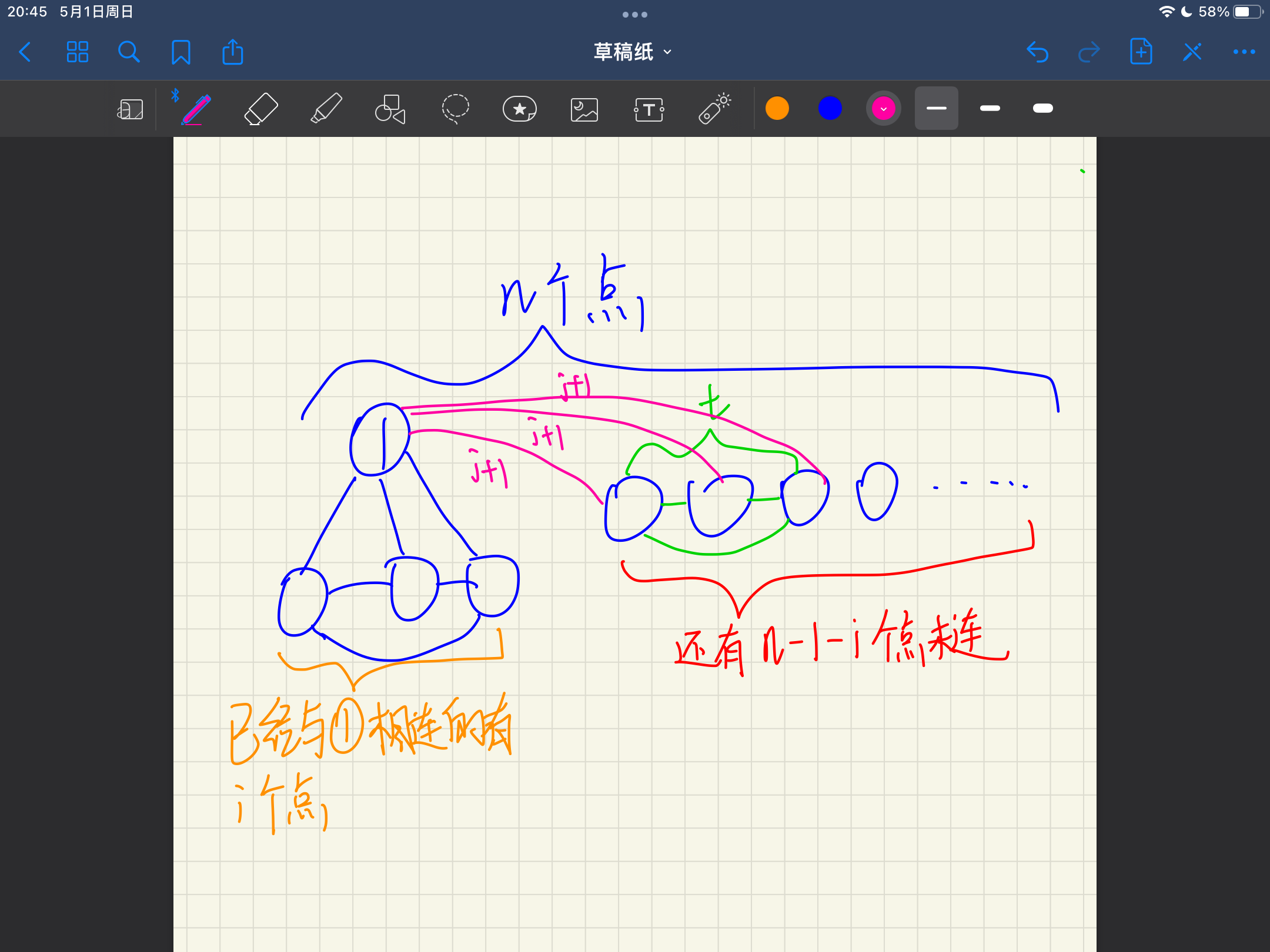
粉红色表示边权为\(i + 1\)的边，绿色表示\(t\)个点内部连线，边权满足\([j + 1, k]\)，连接\(\cfrac{t * (t - 1)}{2}\)条，左边\(i\)个点与右边\(t\)个点相连有\(i * t\)条，边权有\(k - (j + 1) + 1 = k - j\)中选择，所以可以得出状态方程了：

\[f[i + t][j + 1] += f[i][j] * C_{n - 1 - i}^{t} * (k - j)^{t * i + \frac{t * (t - 1)}{2}} \]

结果：\(f[n - 1][k]\)表示往\(1\)结点添加\(n - 1\)个点，最大边权为\(k\)

#include <bits/stdc++.h>

using namespace std;

using ll = long long;

const int Mod = 998244353;
const int N = 300;
ll f[N][N]; //与1相连的点有i个 且最大边权不超过j的方案数
ll C[N][N];

ll qmi(ll a, ll b) {
	ll res = 1;
	while (b) {
		if (b & 1) res = res * a % Mod;
		b >>= 1;
		a = a * a % Mod;
	}

	return res % Mod; 
}

int main() {
	
	int n, k;
	cin >> n >> k;
	for (int i = 0; i < N; i++) {
		for (int j = 0; j <= i; j++) {
			if (!j) C[i][j] = 1;
			else C[i][j] = (C[i - 1][j] + C[i - 1][j - 1]) % Mod;
		}
	}
	f[0][0] = 1;
	for (int i = 0; i <= n - 1; i++) { //已经有i个点合并进来
		for (int j = 0; j <= k; j++) { //最大边权不超过j 
			for (int t = 0; t <= n - i - 1; t++) { //从剩余的点中选t个的边权是i + 1
				f[i + t][j + 1] = (f[i + t][j + 1] + f[i][j] * C[n - 1 - i][t] % Mod * qmi(k - j, t * i + t * (t - 1) / 2) % Mod) % Mod;
			}
		}
	}

	cout << f[n - 1][k] << "\n";

	return 0;
}