P1126 机器人搬重物

题目大意：

一个网格，机器人只能走格点，不能走框内，而障碍物是在框内的，机器人有五个指令：向前走一步、向前走两步、向前走三步、向左转、向右转，每个指令都需要花费1秒中的时间，计算机器人从起点到终点花费的最少时间（原题链接：P1126 机器人搬重物）
如图（图片来自洛谷）：

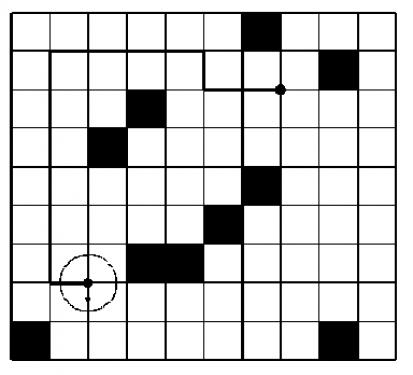
输入格式：

第一行：(N)，(M)表示图大小，接下来(N)行就是图，(0)表示空地，(1)表示障碍物，接下来一行起点(x)，(y)，终点(xx)，(yy)，初始方向(dir)（一个大写字母）：东(E)，南(S)，西(W)，北(N)

输出格式：

一个整数，表示机器人完成任务所需的最少时间。如果无法到达，输出(−1)。

输入：

9 10
0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 0 1 0
0 0 0 1 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 1 0 0 0 0
0 0 0 1 1 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 1 0
7 2 2 7 S

输出：

12

思路：

第一个问题：机器人只能走格点，而障碍物在框内，换句话说就是障碍物的四个顶点机器人都是不可以走的，因此我们可以干脆把原来的图转化成格点图（这个我在做的时候是想到了的。。。）。
转化这个操作在草稿纸上模拟一下就懂了，于是就有了下边的代码。

if(g[i][j] == 1) //转化
{
     mp[i-1][j-1] = 1;
     mp[i-1][j] = 1;
     mp[i][j-1] = 1;
     mp[i][j] = 1;
}

再引用一个图吧~~（来自洛谷题解），

转化后了，就相当于这样。
(BFS)还是挺好写的，这图难就难在方向处理，太蛋疼了，看了那位仁兄的题解才懂的。
大的想法：先枚举四个方向，然后再枚举走1~3步，要注意的是我们切换方向的时候也需要用最短的时间来切换，于是我们就用一个数组来存从当前方向转向到最优方向花的时间，代码如下：

mindi[5] = {0, 1, 2, 1, 0}

再再引用一个图吧~~，比如我们在正北方向，那么转到最优方向的时间如下（题目中我们默认它顺时针转动，不过逆时针也可以啦）：

再就是转向问题了（用(i)枚举四个方向）：用(fdi)数组存方向，用(ffdi)存转动i后的方向。

int fdi[5] = {0, 1, 4, 2, 3}
ffdi[5] = {0, 1, 3, 4, 2}

相关代码：

int ffx = ffdi[t.di] + i; //顺时针旋转i次后后到达的方向编号
if(ffx == 5) ffx = 1;
else if(ffx == 6) ffx = 2;
else if(ffx == 7) ffx = 3;
else if(ffx == 8) ffx = 4;
ffx = fdi[ffx];

比如当前在东(E)方向，也就是方向：(4)，(ffx = ffdi[t.di] + i = ffdi[4] + 1 = 3), (ffx = fdi[3] = 2),顺时针转一下到方向(2)，即南(S)方向。

再枚举1~3步：
类似于(Dijkstra)的判断：(t.res+spin+1 < dist[nx][ny] || dist[nx][ny] == -1 ) && mp[nx][ny] == 0 如果距离更小 或者 没有到达过 并且点可走：更新距离，入队列。

总代码：

#include <iostream>
#include <queue>
#include <cstring>

using namespace std;

const int N = 55, M = 100;

int g[N][N], mp[M][M];
int n, m;
int x, y, xx, yy;
int dist[M][M];
int mindi[5] = {0, 1, 2, 1, 0};
int fdi[5] = {0, 1, 4, 2, 3}, ffdi[5] = {0, 1, 3, 4, 2}; //
int fx[5] = {0, -1, 1, 0, 0}, fy[5] = {0, 0, 0, -1, 1}; //只走x方向 或者只走y方向
int dir; //起点方向

struct node
{
    int sx, sy;
    int di;
    int res;
};

void direction(char *op)
{
    switch(*op)
    {
        case 'N': dir = 1; break;
        case 'S': dir = 2; break;
        case 'W': dir = 3; break;
        case 'E': dir = 4; break;
    }
    return;
}

void bfs(int x, int y)
{
    node start; //起点
    start.sx = x, start.sy = y, start.di = dir, start.res = 0;
    memset(dist, -1, sizeof dist);
    queue<node> q;
    q.push(start);
    dist[x][y] = 0;

    while(q.size())
    {
        node d;
        auto t = q.front();
        q.pop();

        for(int i = 1; i <= 4; i++)
        {
            int spin = mindi[i]; //切换方向的最短旋转次数

            int ffx = ffdi[t.di] + i; //顺时针旋转i次后后到达的方向编号
            if(ffx == 5) ffx = 1;
            else if(ffx == 6) ffx = 2;
            else if(ffx == 7) ffx = 3;
            else if(ffx == 8) ffx = 4;
            ffx = fdi[ffx];
            for(int j = 1; j <= 3; j++) //走1~3步
            {
                int nx = t.sx + fx[ffx] * j, ny = t.sy + fy[ffx] * j;
                if(nx <= 0 || nx >= n || ny <= 0 || ny >= m || ((nx == x) && (ny == y)) || mp[nx][ny] == 1) 
                    break; //起点或者障碍物或者越界
                if((t.res+spin+1 < dist[nx][ny] || dist[nx][ny] == -1 ) &&  mp[nx][ny] == 0)
                {
                    d.sx = nx, d.sy = ny, d.di = ffx, d.res = t.res + spin + 1;
                    dist[nx][ny] = d.res;
                    q.push(d);
                }
            }
        }
    }    
}

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
    {
        for(int j = 1; j <= m; j++)
        {
            cin >> g[i][j];
            if(g[i][j] == 1) //转化
            {
                mp[i-1][j-1] = 1;
                mp[i-1][j] = 1;
                mp[i][j-1] = 1;
                mp[i][j] = 1;
            }
        }
    }
    char op[2];
    cin >> x >> y >> xx >> yy >> op;
    direction(op);
    bfs(x, y);
    
    cout << dist[xx][yy] << endl;
    system("pause");
    return 0;
}

这道绿题花了两个小时的时间(AC)，然后写了一个小时的博客，太菜了，太菜了。。。