二分图（染色法判断二分图 求二分图的最大匹配）

二分图

设(G=(V,E))是一个无向图，如果顶点(V)可分割为两个互不相交的子集((A,B))，并且图中的每条边(（i，j）)所关联的两个顶点(i)和(j)分别属于这两个不同的顶点集((A, B))，则称图(G)为一个二分图。
因此如果一个图是二分图，它一定不含有奇数环。


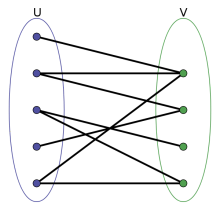
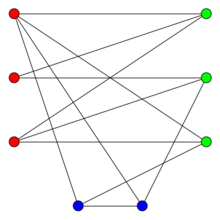
图来自百度百科

染色法判断二分图

给定一个n个点m条边的无向图，图中可能存在重边和自环。

请你判断这个图是否是二分图。

输入格式
第一行包含两个整数n和m。

接下来m行，每行包含两个整数u和v，表示点u和点v之间存在一条边。

输出格式
如果给定图是二分图，则输出“Yes”，否则输出“No”。

数据范围
(1 leq n,m leq 10^5)
输入样例：
4 4
1 3
1 4
2 3
2 4
输出样例：
Yes

思路：

时间复杂度(O(n+m))如果有奇数环，那么染色的过程中则一定会出现矛盾，就是一条边的两个端点一定是不同颜色的，例如

因此这就是个dfs的过程。

代码

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;

const int N = 100010, M = 200010;

int n, m;
int h[N], e[M], ne[M], idx;
int color[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

bool dfs(int u, int c)
{
    color[u] = c;

    for(int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        if(!color[j]) //如果没有被染色
        {
            if(!dfs(j, 3-c)) return false; //3-c: 3-1=2, 3-2=1
        }
        else if(color[j] == c) return false; //如果发生冲突
    }

    return true;
}

int main()
{
    cin >> n >> m;

    memset(h, -1, sizeof h);

    while(m--)
    {
        int a, b;
        cin >> a >> b;
        add(a, b), add(b, a);
    }

    bool flag = true;
    for(int i = 1; i <= n; i++)
    {
        if(!color[i])
        {
            if(!dfs(i, 1)) //说明发生冲突了
            {
                flag = false;
                break;
            }
        }
    }

    if(flag) puts("Yes");
    else puts("No");

    return 0;
}

求二分图最大匹配：匈牙利算法

给定一个二分图，其中左半部包含n1个点（编号1_{n1），右半部包含n2个点（编号1}n2），二分图共包含m条边。

数据保证任意一条边的两个端点都不可能在同一部分中。

请你求出二分图的最大匹配数。

二分图的匹配：给定一个二分图(G)，在(G)的一个子图(M)中，(M)的边集({E})中的任意两条边都不依附于同一个顶点，则称(M)是一个匹配。

二分图的最大匹配：所有匹配中包含边数最多的一组匹配被称为二分图的最大匹配，其边数即为最大匹配数。

输入格式
第一行包含三个整数 n1、 n2 和 m。

接下来m行，每行包含两个整数u和v，表示左半部点集中的点u和右半部点集中的点v之间存在一条边。

输出格式
输出一个整数，表示二分图的最大匹配数。

数据范围
(1 leq n1,n2 leq 500)
(1 leq u leq n1)
(1 leq v leq n2)
(1 leq m leq 10^5)
输入样例：
2 2 4
1 1
1 2
2 1
2 2
输出样例：
2

思路：

举个很形象的例子，相当于男孩女孩找对象，看图（自己做的，很丑陋。。）

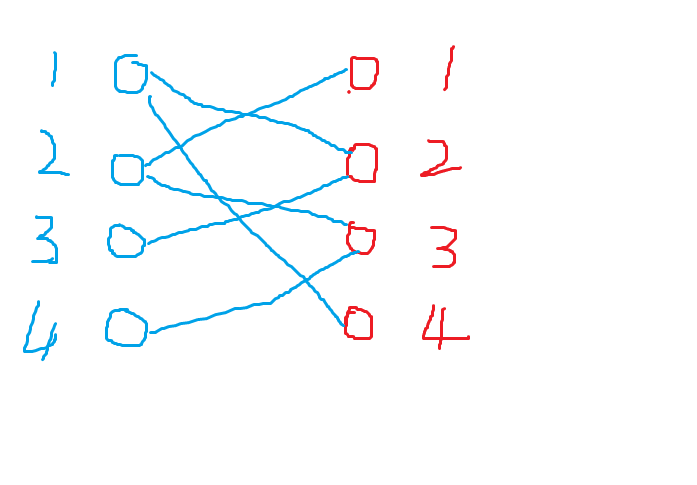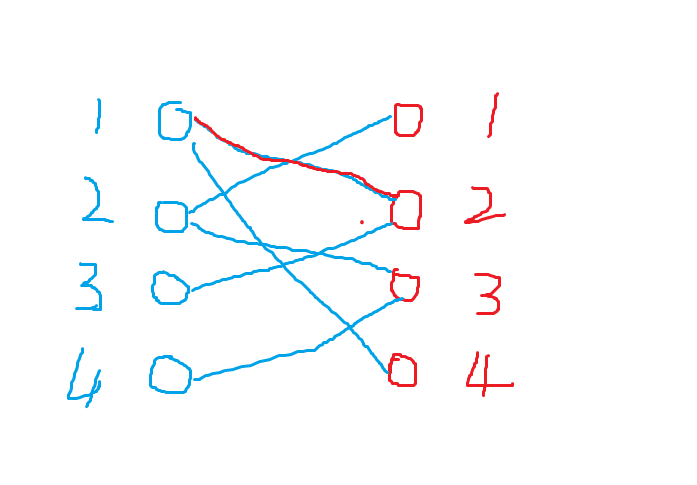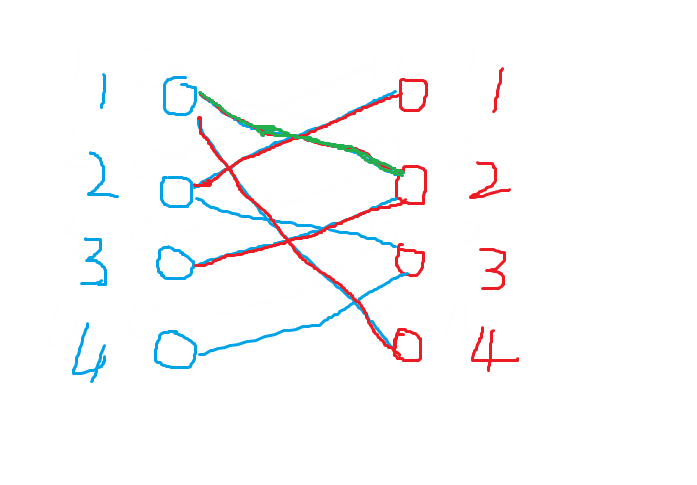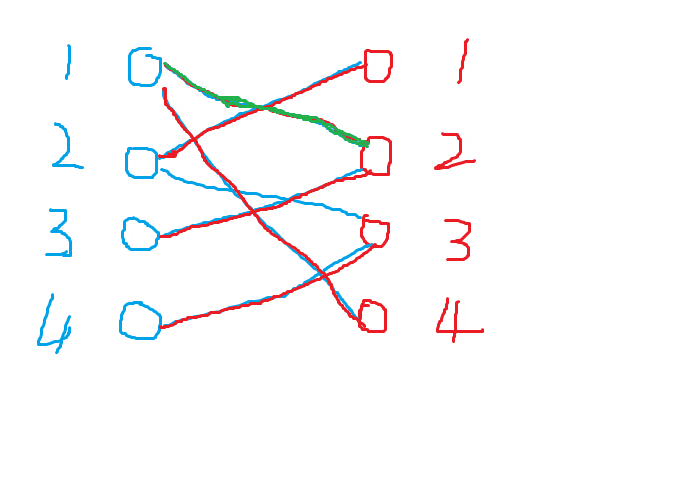
蓝点表示男生，红点表示女生。
从男1开始，先遍历看上的女生（女2，女4），发现女2单身，于是与之牵手，用红线连接。
男2，遍历其看上的女生（女1，女3），发现女1单身，于是与之牵手。
男3，只看上了女2，但是发现其已经有对象了，但是他没有放弃，勇敢追求，终于追上了女2，于是男1就被绿了，（我们根据女2找到男1给他匹配对象），但是男一还有备胎，于是与女4牵手。（男1的经历就体现了匈牙利算法核心）
男4，只看上了女3，并发现她单身，牵手，所有男生都找到了对象。
匹配完毕，于是最大匹配就是4。
所以：对于一件事，想做就勇敢的去做，做错比错过要好。-----yxc（哈哈哈）

代码

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 510, M = 100010;
int n1, n2, m;
int h[N], e[M], ne[M], idx;
int match[N];
bool st[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

bool find(int x)
{
    for(int i = h[x]; i != -1; i = ne[i]) //遍历这个当前男孩子看上的女孩子
    {
        int j = e[i];
        if(!st[j]) //如果之前没有考虑过
        {
            st[j] = true;//先做标记
            if(match[j] == 0 || find(match[j])) //妹子没有匹配到一个男生 或者 可以为当前妹子找到下家男生 这个妹子就空出来了
            {
                match[j] = x;
                return true;
            }
        }
    }   
    return false;
}

int main()
{
    ios::sync_with_stdio(false), cin.tie(0);
    
    cin >> n1 >> n2 >> m;
    memset(h, -1, sizeof h);
    while(m--)
    {
        int a, b;
        cin >> a >> b;
        add(a, b);
    }

    int res = 0;
    for(int i = 1; i <= n1; i++) //遍历每一个点
    {
        memset(st, false, sizeof st);
        if(find(i)) res++;
    }

    cout << res << endl;

    return 0;
}