软件工程实践2017第二次作业

作业链接
GitHub：Sudoku

解题思路：

    这次作业，用的时间并没有很多，开学前基本都在走亲戚加上在家比较懒散，只有几个零散的下午。开始看题目后，在纸上写写画画，感觉可以通过生成一个3x3的宫，然后通过这个宫去进行行列变换，这样就可以得到整个数独盘，实践的时候发觉这样子变换的话代码似乎很难写，搜索了一下，发现有一种简便写法（真是简练又巧妙ORZ）,依葫芦画瓢，从两种扩充到八种，写完后却发现我的方案数不够。由于首位置固定，那么全排列方案数就只有 8！，每个排列有8种变换规则（暂时想到8种 拿123 456 789作为3x3的一宫，其他变换规则为123 789 456 | 132 798 465 | 132 465 798 | 147 258 369 | 147 369 258 | 174 285 396 | 174 396 285），因此总的方案数就只有322560种。以下是此种方法的代码

#include<bits/stdc++.h>
using namespace std;

const int tran1[3][3] = {{0,1,2},{1,2,0},{2,0,1}}; 
const int tran2[3][3] = {{0,1,2},{2,0,1},{1,2,0}};  
const int tran3[3][3] = {{0,2,1},{2,1,0},{1,0,2}};
const int tran4[3][3] = {{0,2,1},{1,0,2},{2,1,0}};

int a[10] = {6,1,2,3,4,5,7,8,9};
int sudoku[3][3];

void show1(const int tran[][3]){
	for (int i = 0;i < 9;i++){
		for (int j = 0;j < 9;j++){
			printf("%2d",sudoku[tran[j/3][i%3]][tran[i/3][j%3]]);
		}
		cout << endl;
	}
	cout << endl << endl;
}

void show2(const int tran[][3]){
	for (int i = 0;i < 9;i++){
		for (int j = 0;j < 9;j++){
			 printf("%2d",sudoku[tran[i/3][j%3]][tran[j/3][i%3]]); 
		}
		cout << endl;
	}
	cout << endl << endl;
}


int main(){
	//freopen("output.txt","w",stdout);
	int n,cnt = 0;
	cin >> n;
	do
	{
		if (cnt == n)	break;
		for (int i = 0;i < 3;i++)	for (int j = 0;j < 3;j++)	sudoku[i][j] = a[3*i + j];
		if (cnt + 8 <= n){
			show1(tran1);show2(tran1);
			show1(tran2);show2(tran2);
			show1(tran3);show2(tran3);
			show1(tran4);show2(tran4);
			cnt += 8;
		}else {
			int x = n - cnt;
			switch(x){
				case 7:show1(tran1),cnt++;
				case 6:show2(tran1),cnt++;
				case 5:show1(tran2),cnt++;
				case 4:show2(tran2),cnt++;
				case 3:show1(tran3),cnt++;
				case 2:show2(tran3),cnt++;
				case 1:show1(tran4),cnt++;
			}
		}
		
	}while (next_permutation(a + 1,a + 9));
	return 0;
}

    此种方法走不通后，在进一步查资料的过程，找到一篇文章

根据文章描述的生成算法，如果按照1-9遍历搜索会导致每次生成的数独盘与第一次生成的相同，因此将这步改成随机1-9中的某数开始搜索。

设计实现

• Sudoku类用来生成数独盘，包括三个函数：generateBoard(int,int)是生成数独的核心，validNum(int) 用来判断随机的数是否符合数独规则，displayBoard(ofstream &)（后续优化 I/O操作时改成了displayBoard()）则是打印数独终盘到文件；
• Process类用来处理命令行传入的参数，包含两个函数：isNumber(char* ) 用来判断传入的字符串是否是纯数字，convertToNum(char* )用来将传入的字符串转化为数字。

代码说明

以下代码是生成数独的核心代码

• 数独首位置被固定，我的是被固定为6，因此按照我的搜索策略，我从第一行第二列开始搜索
• 判断数独是否填完，没有则按照从左到右，从上到下的顺序搜索
• 随机一个数val，按照val-9，1-val顺序进行检测（调用validNum(int row,int col,int num)检测），找到符合的数字则填空，跳到步骤1
• 若所有数都不符合数独规则，则返回上一个空，将值置为0，继续搜索可能解，跳至步骤1
• 生成整个终盘

bool Sudoku::generateBoard(int row, int col) {
	//终止条件 
	if (row == 8 && col == 9) {
		return true;
	}

	//按列填，填满一列，换行 
	if (col == 9) {
		row++;
		col = 0;
	}


	int randNum = (rand() % 9) + 1;
	//int randNum = e() % 9 + 1;

	for (int i = randNum; i <= 9; i++) {
		if (validNum(row, col, i)) {
			board[row][col] = i;

			//回溯 
			if (generateBoard(row, col + 1)) {
				return true;
			}
			else {
				board[row][col] = 0;
			}

		}
	}

	for (int i = randNum; i > 0; i--) {
		if (validNum(row, col, i)) {
			board[row][col] = i;

			//回溯 
			if (generateBoard(row, col + 1)) {
				return true;
			}
			else {
				board[row][col] = 0;
			}
		}
	}

	return false;
}

另外，十分感谢助教在整个实践过程的帮助。一开始，我的数独终盘在单次运行的时候，生成的每一个数独都是一样的，但是不同次运行的数独不一样。改了一下午都没思绪，一直以为是伪随机的问题，用时间做随机种子，时间精度不够，然后在网上找了很多随机方法来进一步提高时间精度，或者是每次运行生成随机种子其一，其二等等，但是都没有解决这个问题，最后在助教帮助下，我每次生成的时候没有将上一次数组中的棋盘数据清空，导致了这个问题。

测试运行

此外，找到的这篇文章还顺带讲了生成唯一解初盘的生成的方法，正好对应了附加题，但是这个方法的结论我还没想懂是怎么来的。。。

PSP

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划	20	30
· Estimate	· 估计这个任务需要多少时间	20	30
Development	开发	560	860
· Analysis	· 需求分析 (包括学习新技术)	180	300
· Design Spec	· 生成设计文档	0	0
· Design Review	· 设计复审 (和同事审核设计文档)	0	0
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	20	20
· Design	· 具体设计	60	60
· Coding	· 具体编码	90	120
· Code Review	· 代码复审	60	60
· Test	· 测试（自我测试，修改代码，提交修改）	150	300
Reporting	报告	120	70
· Test Report	· 测试报告	30	30
· Size Measurement	· 计算工作量	30	20
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	60	20
合计		700	960

性能测试

为了便于项目的调试运行，我将项目中配置属性的命令行参数设为 -c 10000（上传至GitHub的项目也包括这一设置）
下图是运行数据量为10000的分析报告


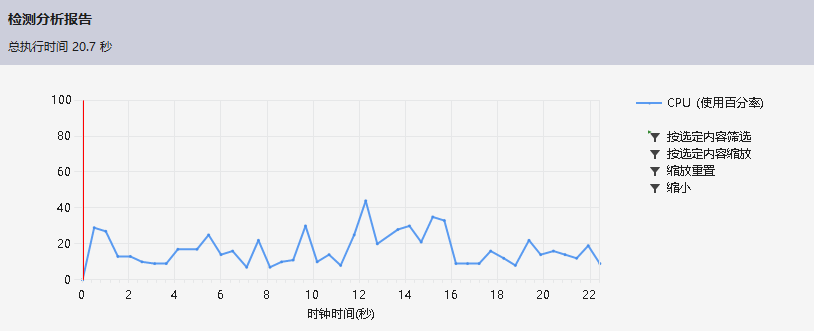
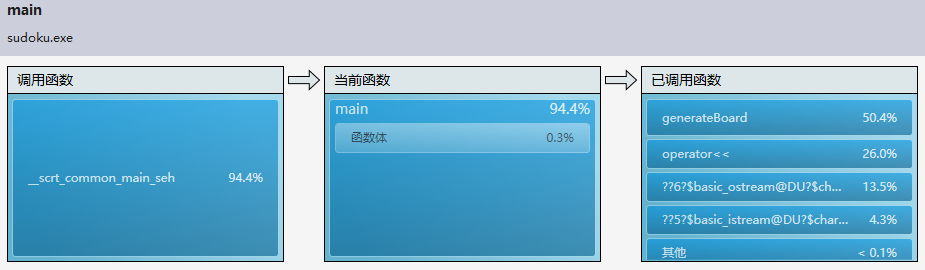
从图中可以看出，生成数独终盘的核心函数generateBoard(int row,int col)占比50%左右，而另外占了一大半时间的为I/O操作。


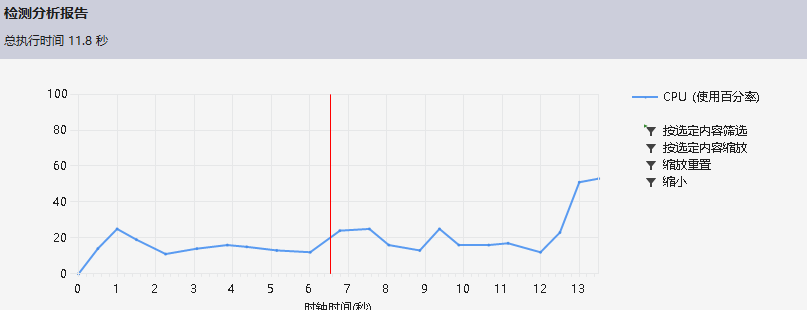
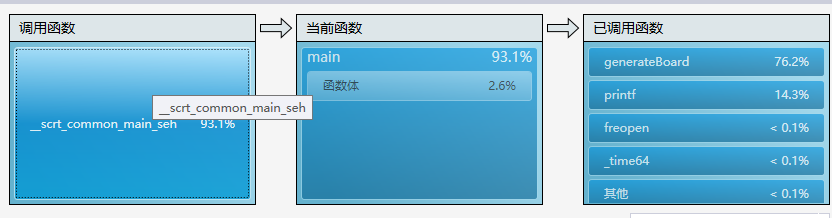
之前有听别人说过，C系文件操作的可能会比C++的快，因此我尝试着将I/O操作改成C系函数。将I/O操作函数改成C系的函数后，同样是10000的数据量，但是时间缩短了将近一半。改成freopen进行读写时，VS提示不安全，建议使用freopen_s，查阅了资料后，成功改成C系函数。

void Sudoku::displayBoard() {
	for (int i = 0; i < 9; i++) {
		for (int j = 0; j < 9; j++) {
			//j ? fout << " " << board[i][j] : fout << board[i][j];
			j ? fprintf(stdout,"%2d", board[i][j]) : fprintf(stdout,"%d", board[i][j]);
		}
		fprintf(stdout,"
");
		//fout << endl;
	}
	fprintf(stdout,"
");
	//fout << endl;
}

//main部分
FILE *stream;
freopen_s(&stream, "sudoku.txt", "w", stdout);
//ofstream fout;
//fout.open("./sudoku.txt");
int n = process.convertToNum(argv[2]);
srand((unsigned int)time(NULL));
while (n--) {
    Sudoku sudoku;
    sudoku.generateBoard(0, 1);
    //sudoku.displayBoard(fout);
    sudoku.displayBoard();
    }
//fout.close();

对于调用者/被调用者关系


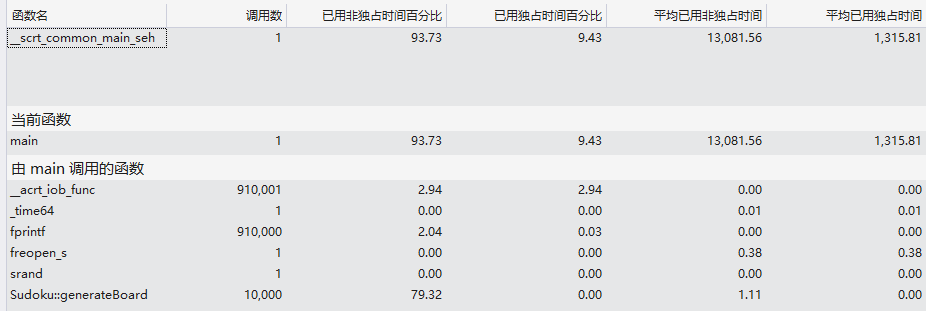
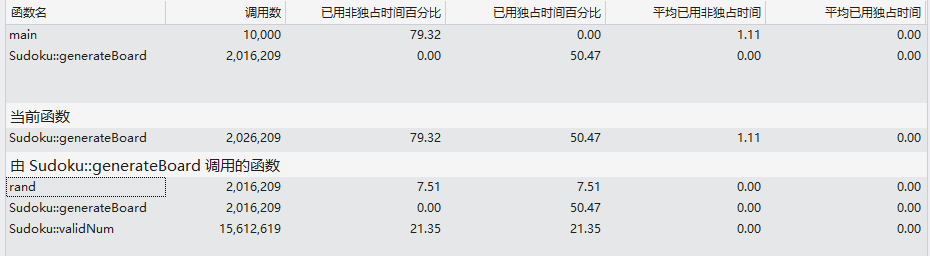
以上图中，generateBoard(int,int)在程序中占用的时间占了绝大部分，但是此部分暂时还没有能力想到如何去优化。对于validNum(int,int,int)调用次数之多，但是如果通过改写这个函数使之包含在generateBoard(int,int)函数中，将破坏代码可读性，因此没有考虑将validNum(int,int,int)的功能直接在generateBoard(int,int)中处理。

    此外，代码覆盖率还没弄成功，之前试了AxoCover，ReSharper都没有在VS2017社区版成功使用，今天助教新给的C++ Coverage Validator x64还没搞懂怎么用。而单元测试之前看了知道了大概是怎么一回事，但是到了今天也只会写一些简单的Assert::AreEqual()判断