稀疏子空间聚类综述
摘要：本文对已有稀疏子空间聚类方法的模型、算法和应用等方面进行详细阐述, 并分析存在的不足, 指出进一步研究的方向 。
稀疏子空间聚类：
1.对于给定的一组数据，建立子空间表示模型
2.寻找数据在低维子空间中的表示系数
3.根据表示系数矩阵构造相似度矩阵（也称关联矩阵：用一个矩阵来表示各个点和每条边之间的关系）
4.最后利用谱聚类方法，如规范化割 (Normalized cut, Ncut)获得数据的聚类结果
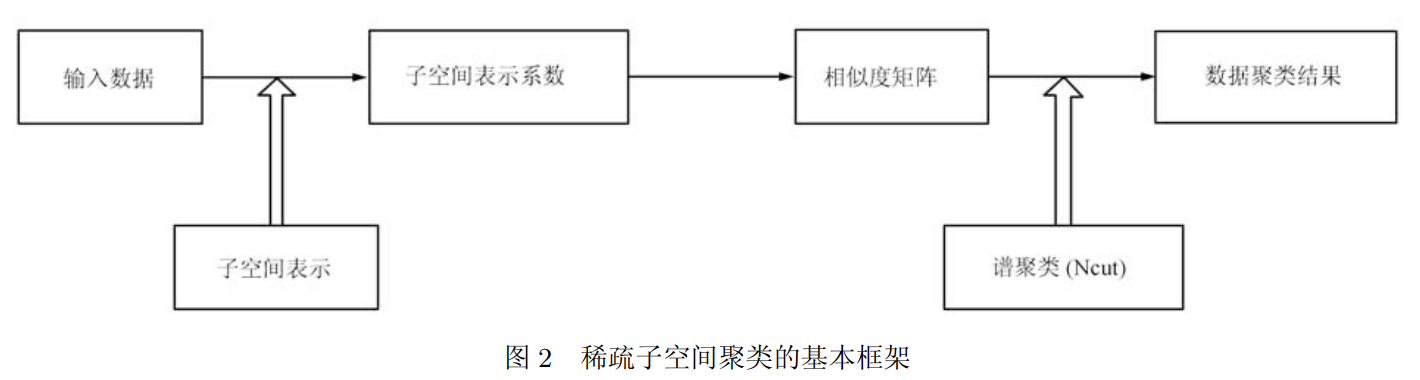
利用数据在特定空间的稀疏性更有效地表示数据或揭示数据的本质特征
基本思想：将数据
表示为所有其他数据的线性组合
一般地, 稀疏子空间聚类模型可以统一描述为如下优化问题 ：
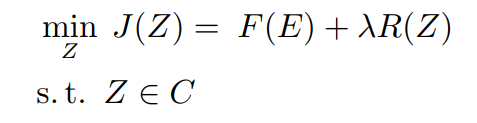
稀疏子空间的研究主要围绕以下几个方面:
（1) 正则项 R(Z) 的设计, 目的是使得子空间表示系数矩阵具有良好的有利于子空间聚类的结构
（2) 数据项 F (E) 的设计, 使其对各种噪声鲁棒
（3) 快速算法的设计
（4) 应用方面的探索
在一定条件下，SSC和LLR的模型分别采用稀疏和低秩正则项保证了表示系数矩阵的块对角结构，但SSC的模型得到的子空间表示系数矩阵可能过于稀疏，LLR型得到的子空间表示系数矩阵可能不稀疏，针对这些问题，后续提出了一系列改进的模型和方法。
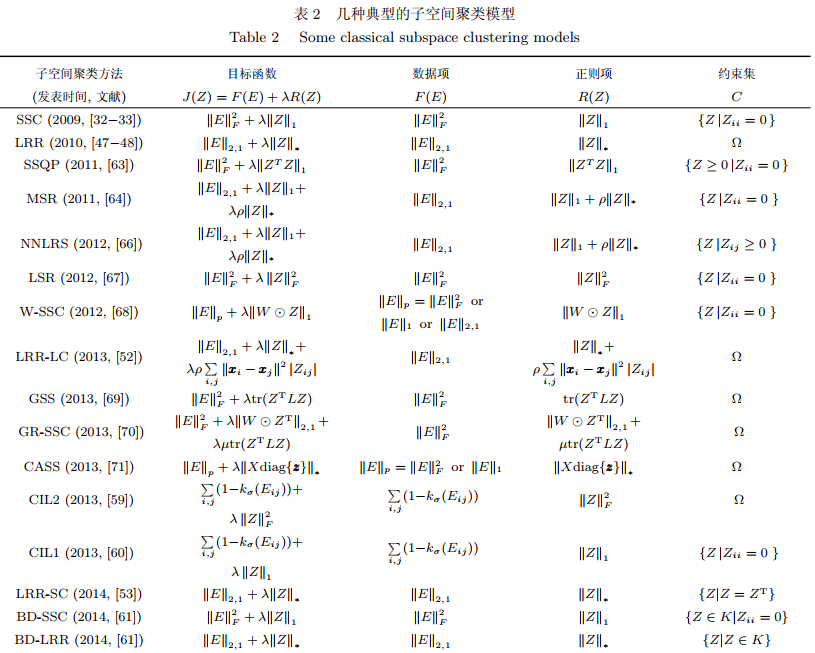
稀疏子空间聚类的性能取决于两个方面:
一方面, 模型对各种噪声、 数据缺损、 奇异数据的鲁棒性取决于数据项;
另一方面, 子空间表示系数矩阵的结构取决于正则项. 现有模型选择不同的度量来设计数据项与正则项, 存在一定的局限性。