二分图及其匹配的基本问题
不务正业系列,简单写一下二分图作业里的题解。课件剽窃自Y老师(老师别打我)
二分图
概念
二分图又称作二部图,是图论中的一种特殊模型。
设 (G=(V,E)) 是一个无向图,如果顶点(V)可分割为两个互不相交的子集((A,B)),并且图中的每条边((i,j))所关联的两个顶点 (i) 和 (j) 分别属于这两个不同的顶点集((i_{A},j_{B})),则称图(G)为一个二分图。(——from) 百度百科
-
二分图:通俗地来讲,把一个图的顶点划分为两个不相交集
U和V,使得每一条边都分别连接U、V中的顶点。如果存在这样的划分,则此图为一个二分图。二分图的一个等价定义是:不含有「含奇数条边的环」的图。图1是一个二分图。为了清晰,我们以后都把它画成图2的形式。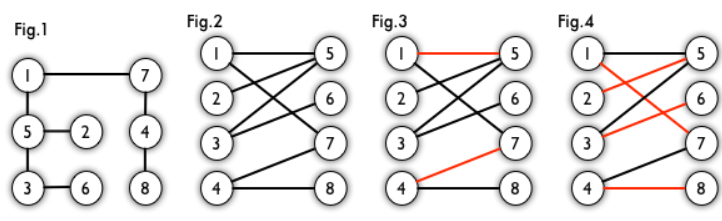
-
匹配:在图论中,一个「匹配」(
matching)是一个边的集合,其中任意两条边都没有公共顶点。例如,图3、图4中红色的边就是图2的匹配。 -
我们定义匹配点、匹配边、未匹配点、非匹配边,它们的含义非常显然。例如图
3中1、4、5、7为匹配点,其他顶点为未匹配点;(1,5)、(4,7)为匹配边,其他边为非匹配边。 -
最大匹配:一个图所有匹配中,所含匹配边数最多的匹配,称为这个图的最大匹配。图
4是一个最大匹配,它包含4条匹配边。 -
完美匹配:如果一个图的某个匹配中,所有的顶点都是匹配点,那么它就是一个完美匹配。图
4是一个完美匹配。显然,完美匹配一定是最大匹配(完美匹配的任何一个点都已经匹配,添加一条新的匹配边一定会与已有的匹配边冲突)。但并非每个图都存在完美匹配。 -
举例来说:如下图所示,如果在某一对男孩和女孩之间存在相连的边,就意味着他们彼此喜欢。是否可能让所有男孩和女孩两两配对,使得每对儿都互相喜欢呢?图论中,这就是完美匹配问题。如果换一个说法:最多有多少互相喜欢的男孩/女孩可以配对儿?这就是最大匹配问题。

匈牙利算法
求解最大匹配问题的一个算法是匈牙利算法
- 交替路:从一个未匹配点出发,依次经过非匹配边、匹配边、非匹配边…形成的路径叫交替路。如图
5中9→4→8→1→6→29→4→8→1→6→2 就是一条交替路。
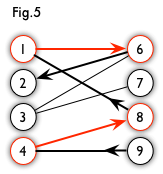
-
增广路:从一个未匹配点出发,走交替路,如果途径另一个未匹配点(出发的点不算),则这条交替路称为增广路((Agumenting) (Path))。例如,图
5中的一条增广路如图6所示(图中的匹配点均用红色标出):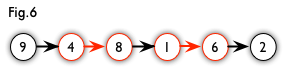
- 增广路有一个重要特点:非匹配边比匹配边多一条。因此,研究增广路的意义是改进匹配。
- 只要把增广路中的匹配边和非匹配边的身份交换即可。
- 由于中间的匹配节点不存在其他相连的匹配边,所以这样做不会破坏匹配的性质。
- 交换后,图中的匹配边数目比原来多了
1条。 - 我们可以通过不停地找增广路来增加匹配中的匹配边和匹配点。找不到增广路时,达到最大匹配(这是增广路定理)。匈牙利算法正是这么做的。在给出匈牙利算法
DFS和BFS版本的代码之前,先讲一下匈牙利树。
-
匈牙利树:一般由
BFS构造(类似于BFS树)。从一个未匹配点出发运行BFS(唯一的限制是,必须走交替路),直到不能再扩展为止。例如,由图7,可以得到如图8的一棵BFS树: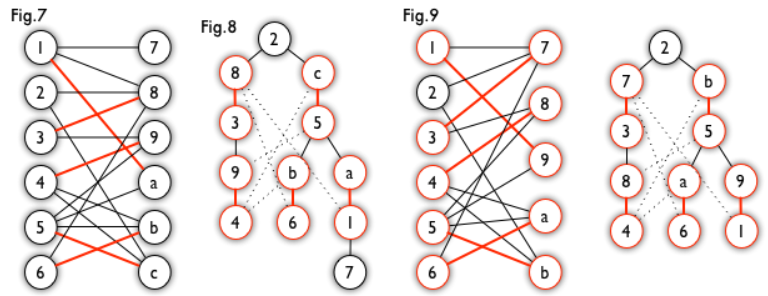
- 这棵树存在一个叶子节点为非匹配点(
7号),但是匈牙利树要求所有叶子节点均为匹配点,因此这不是一棵匈牙利树。如果原图中根本不含7号节点,那么从2号节点出发就会得到一棵匈牙利树。这种情况如图9所示(顺便说一句,图8中根节点2到非匹配叶子节点7显然是一条增广路,沿这条增广路扩充后将得到一个完美匹配)。
- 这棵树存在一个叶子节点为非匹配点(
补充定义和定理:
- 最大匹配数:最大匹配的匹配边的数目
- 最小点覆盖数:选取最少的点,使任意一条边至少有一个端点被选择
- 最大独立数:选取最多的点,使任意所选两点均不相连
- 最小路径覆盖数:对于一个 DAG(有向无环图),选取最少条路径,使得每个顶点属于且仅属于一条路径。路径长可以为 0(即单个点)。
- 定理
- 定理一:最大匹配数 = 最小点覆盖数(这是 Konig 定理)
- 定理2:最大匹配数 = 最大独立数
- 定理3:最小路径覆盖数 = 顶点数 - 最大匹配数
一些小题的简单题解
超级英雄Hero
题目描述
现在电视台有一种节目叫做超级英雄,大概的流程就是每位选手到台上回答主持人的几个问题,然后根据回答问题的多少获得不同数目的奖品或奖金。
主持人问题准备了若干道题目,只有当选手正确回答一道题后,才能进入下一题,否则就被淘汰。为了增加节目的趣味性并适当降低难度,主持人总提供给选手几个“锦囊妙计”,比如求助现场观众,或者去掉若干个错误答案(选择题)等等。
这里,我们把规则稍微改变一下。假设主持人总共有m道题,选手有n种不同的“锦囊妙计”。主持人规定,每道题都可以从两种“锦囊妙计”中选择一种,而每种“锦囊妙计”只能用一次。我们又假设一道题使用了它允许的锦囊妙计后,就一定能正确回答,顺利进入下一题。
现在我来到了节目现场,可是我实在是太笨了,以至于一道题也不会做,每道题只好借助使用“锦囊妙计”来通过。如果我事先就知道了每道题能够使用哪两种“锦囊妙计”,那么你能告诉我怎样选择才能通过最多的题数吗?
输入格式
输入文件的一行是两个正整数n和m(0 < n <1001,0 < m < 1001)表示总共有n中“锦囊妙计”,编号伟0~n-1,总共有m个问题。
以下的m行,每行两个数,分别表示第m个问题可以使用的“锦囊妙计”的编号。
注意,每种编号的“锦囊妙计”只能使用一次,同一个问题的两个“锦囊妙计”可能一样。
输出格式
第一行为最多能通过的题数p
样例
样例输入
5 6
3 2
2 0
0 3
0 4
3 2
3 2
样例输出
4
一道练手的板子题,有一个坑点是只要答错一道题就全部GG了,所以不要跑完匈牙利,一个点不行直接break掉。
代码:
#include <cstdio>
#include <vector>
#include <cstring>
#include <algorithm>
#include <iostream>
using namespace std;
const int maxn=5000+20;
bool vis[maxn];
int head[maxn],len,a[maxn];
struct Edge{
int to,next;
}edge[maxn<<1];
void Add(int u,int v){
edge[++len].to=v;
edge[len].next=head[u];
head[u]=len;
}
bool Find(int u){
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(!vis[v]){
vis[v]=1;
if(a[v]==-1||Find(a[v])){
a[v]=u;
return 1;
}
}
}
return 0;
}
int n,m;
int main(){
scanf("%d%d",&n,&m);
int u,v;
for(int i=1;i<=m;i++){
scanf("%d%d",&u,&v);
Add(i,u+m),Add(i,v+m);
}
memset(a,-1,sizeof(a));
int cnt=0;
for(int i=1;i<=m;i++){
memset(vis,0,sizeof vis);
if(Find(i)) cnt++;
else break;
}
cout<<cnt<<endl;
return 0;
}
放置机器人(place the robot)
题目描述
Robert是一位著名的工程师。一天他的老板给了他一个任务。任务的背景如下:
给出一张由方块组成的地图。方块有许多种:墙,草,和空地。老板想让Robert在地图上放置尽可能多的机器人。每个机器人拿着一把激光枪,它可以同时向东西南北四个方向射击。机器人必须一直呆在它开始时被放在的位置并且不断地射击。激光束当然可以经过空地或草地,但不能穿过墙。机器人只能被放在空地上。
当然老板不希望看到机器人相互攻击。换句话说,两个机器人不能被放在一条线上(竖直或水平),除非它们中间有一堵墙。
由于你是一位机智的程序员和Robert的好基友之一,他请你帮他解决这个问题。也就是说,给出地图的描述,计算地图上最多能放置的机器人数量。
输入格式
输入文件的第一行有两个正整数m,n(1<=m,n<=50),即地图的行数和列数。
接下来有m行,每行n个字符,这些字符是#,*或o,它们分别代表墙,草和空地。
输出格式
输出一行一个正整数,即地图中最多放置的机器人数目
样例
样例输入
sample 1:
4 4
o***
*###
oo#o
***o
sample 2:
4 4
#ooo
o#oo
oo#o
***#
样例输出
sample 1:
3
sample 2:
5
整活
这道题的建图挺不好想的,看了看别人的想法。我们分水平、竖直两个方向来考虑。首先是竖直方向,对于同一列上的空地,只要中间没有墙,我们都可以把他们编到一起成为一个块。然后是水平方向,对于同一行上的空地,只要中间没有墙阻隔,我们也可以把把他们编到一起成为一个块。水平的块,竖直的块就可以看成二分图的X部,Y部,如果两个水平竖直的块中有公共的空地,就连边,然后跑最大匹配即可。
下面是详细的题解,转自:https://blog.csdn.net/u014141559/article/details/44409255
———————————————————————————————————————————————————————————————————————
在问题的原型中,草地,墙这些信息不是本题所关心的,本题关心的只是空地和空地之间的联系。因此,很自然想到了下面这种简单的模型:以空地为顶点,在有冲突的空地间连边。

把所有的空地用数字标明,得到a图:
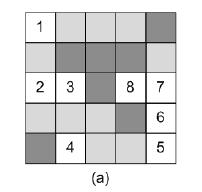
把所有有冲突的空地间用边连接后得到图(b):
于是,问题转化为求图的最大独立集问题:求最大顶点集合,集合中所有顶点互不连接(即互不冲突)。但是最大点独立集问题是一个NP 问题,没有有效的算法能求解。
———————————————————————————————————————————————————————————————————————
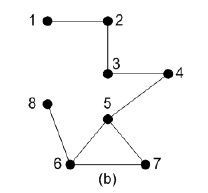
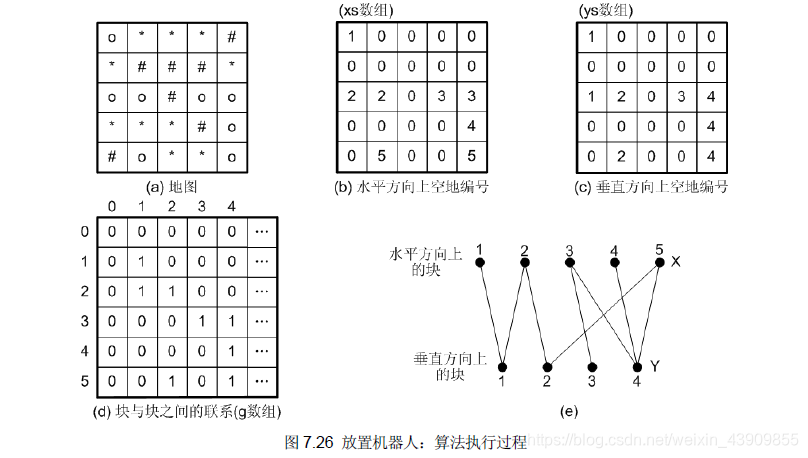
将每一行被墙隔开、且包含空地的连续区域称作“块”。显然,在一个块之中,最多只能放一个机器人。把这些块编上号,如图7.25(a)所示。需要说明的是,最后一行,即第4 行有两个空地,但这两个空地之间没有墙壁,只有草地,所以这两个空地应该属于同一“块”。同样,把竖直方向的块也编上号,如图7.25(b)所示。
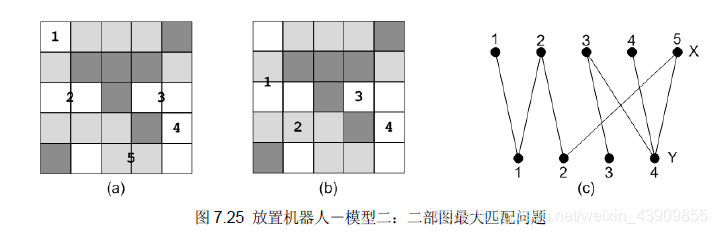
把每个横向块看作二部图中顶点集合X 中的顶点,竖向块看作集合Y 中的顶点,若两个块有公共的空地(注意,每两个块最多有一个公共空地),则在它们之间连边。例如,横向块2 和竖向块1 有公共的空地,即(2, 0),于是在X 集合中的顶点2 和Y 集合中的顶点1 之间有一条边。这样,问题转化成一个二部图,如图7.25©所示。由于每条边表示一个空地(即一个横向块和一个竖向块的公共空地),有冲突的空地之间必有公共顶点。例如边(x1, y1)表示空地(0, 0)、边(x2, y1)表示空地(2, 0),在这两个空地上不能同时放置机器人。所以问题转化为在二部图中找没有公共顶点的最大边集,这就是最大匹配问题。
以上面给的样例的构造结果:
我的蒟蒻代码
前向星写崩了,直接无视前向星部分吧。。。
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#define ll long long
using namespace std;
const int maxn=1000;
struct Edge{
int next,to;
}e[maxn<<5];
int head[maxn],len=0;
void Add(int u,int v){
e[++len].next=head[u];
e[len].to=v;
head[u]=len;
}
vector<int> a[maxn];
int girl[maxn];
bool vis[maxn];
bool Find(int u){
for(int i=0;i<a[u].size();i++){
int v=a[u][i];
if(!vis[v]){
vis[v]=1;
if(girl[v]==-1||Find(girl[v])){
girl[v]=u;
return 1;
}
}
}
return 0;
}
int block_hang,block_lie,f_hang[maxn][maxn],f_lie[maxn][maxn];
char ch[maxn][maxn];
int main(){
int n,m;
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
scanf(" %c",&ch[i][j]);
for(int i=1;i<=n;i++)//开始找水平方向的块
for(int j=1;j<=m;j++){//j是列
if(ch[i][j]=='o'){
block_hang++;
while(ch[i][j]=='o'||ch[i][j]=='*'){
if(ch[i][j]=='o')
f_hang[i][j]=block_hang;
j++;//列右挪一
}
}
}
for(int i=1;i<=m;i++)//开始找竖直方向的块
for(int j=1;j<=n;j++){//j为行
if(ch[j][i]=='o'){//这里是ch[j][i],因为我们开始存的时候是行对列
block_lie++;
while(ch[j][i]=='o'||ch[j][i]=='*'){
if(ch[j][i]=='o')
f_lie[j][i]=block_lie;
j++;//行下挪一
}
}
}
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(ch[i][j]=='o'){
a[f_hang[i][j]].push_back(f_lie[i][j]);//行向列连边
}
int cnt=0;
memset(girl,-1,sizeof girl);
for(int i=1;i<=block_hang;i++){
memset(vis,0,sizeof vis);
cnt+=Find(i);
}
cout<<cnt<<endl;
return 0;
}
封锁阳光大学
题目描述
曹是一只爱刷街的老曹,暑假期间,他每天都欢快地在阳光大学的校园里刷街。河蟹看到欢快的曹,感到不爽。河蟹决定封锁阳光大学,不让曹刷街。
阳光大学的校园是一张由 (n) 个点构成的无向图,(n) 个点之间由 (m) 条道路连接。每只河蟹可以对一个点进行封锁,当某个点被封锁后,与这个点相连的道路就被封锁了,曹就无法在这些道路上刷街了。非常悲剧的一点是,河蟹是一种不和谐的生物,当两只河蟹封锁了相邻的两个点时,他们会发生冲突。
询问:最少需要多少只河蟹,可以封锁所有道路并且不发生冲突。
输入格式
第一行两个正整数,表示节点数和边数。 接下来 (m) 行,每行两个整数 (u,v),表示点 (u) 到点 (v) 之间有道路相连。
输出格式
仅一行如果河蟹无法封锁所有道路,则输出 (Impossible),否则输出一个整数,表示最少需要多少只河蟹。
输入输出样例
输入 #1
3 3
1 2
1 3
2 3
输出 #1
Impossible
输入 #2
3 2
1 2
2 3
输出 #2
1
简单解释
挺巧妙的一道题,虽然跟二分图的关系并不大,通过读题我们知道:
1. 每一条边的两个端点要有一个被占有
2. 两个端点中只能有一个被占有
然后我们就可以将问题巧妙地转化为用两种颜色来给整张图染色(可能有多个连通块),且相邻点颜色不同,根据颜色来解决一些问题。剩下的看代码注释就好
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <vector>
#include <queue>
#include <cmath>
using namespace std;
#define ll long long
#define Game return
#define Over 0
#define dl double
inline int read(){
int s = 0, w = 1;
char c = getchar();
while(c < '0' || c > '9'){if(c == '-') w = -1; c = getchar();}
while(c >= '0' && c <= '9') s = s * 10 + c - '0', c = getchar();
return s * w;
}
const int maxn = 10000 + 10;
const int maxm = 100000 + 10;
struct edge{
int nex, w, to;
}e[maxm << 1];
int head[maxn], len = 0;
void Add(int u, int v){
e[++len].to = v;
e[len].nex = head[u];
head[u] = len;
}
int sum[3], belong[maxn], ans;
bool vis[maxn];
int Dfs(int x, int color){//用0和1代表两种染色,相邻的点染色必须不同
if(vis[x]){//如果该点已经染过色
if(belong[x] != color) return 0;//当前染色与之前染色不同,非法
return 1;
}
vis[x] = 1;//标记为已经染色
belong[x] = color;//记录该点的染色情况
sum[color]++;//某一颜色的点数++
for(int i = head[x]; i; i = e[i].nex){//遍历连边
int v = e[i].to;
if(!Dfs(v, 1 - color)) return 0;
}
return 1;
}
int n, m;
int main(){
n = read(), m = read();
int u, v;
for(int i = 1; i <= m; i++){
u = read(), v = read();
Add(u, v);
Add(v, u);
}
int flag = 0;
for(int i = 1; i <= n; i++){//整个图可能不联通,1到n遍历一下
if(!vis[i]){
sum[0] = sum[1] = 0;//每一个新连通块初始化一下
if(!Dfs(i, 0)){
printf("Impossible
");
return 0;
}
ans += min(sum[0], sum[1]);//每个连通块我们都要涂数量少的那个颜色
}
}
//cout << min(sum[0], sum[1]) << endl; 不能这样写,因为不一定所有块都涂一个颜色
cout << ans << endl;
Game Over;
}