一道有趣的组合数学题
这道题其实挺水的至少没有黑题难度(滑稽 只要学过点组合数学就没太大问题。不过思路还是比较巧妙,值得一做。
讲思路吧。
题意如图:(建筑编号从左到右依次排列)
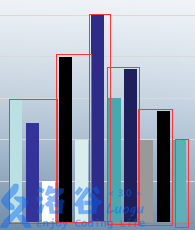
解释一下,画红框的是表示这个红框内的建筑都由一个最高建筑“代表”。比如从左看,(1)号建筑挡住了(2,3)号建筑,直到(4)号建筑比(1)号高,(4)号建筑再成为下一群建筑的代表。
那么给定从最左边看能看到(A)个建筑,从最右边看能看到(B)个建筑,如何求方案数呢?
接下来就是本题的核心了。
我们会发现,当一群数量为(k)的建筑的“代表”确定后,除去代表的剩下(k-1) 个建筑就可以随意排列,那么就有((k-1)!) 种方案,那么就等价于这(k)个建筑的圆排列。除去整个序列中最高的那个建筑,左边看有(A-1) 群建筑,右边看有(B-1) 群建筑。总共有(A+B-2) 群建筑,那么也就有(A+B-2) 个圆排列。
然后。。。有没有想到第一类斯特林数!在这题中就是(n) 个人,(A+B-2) 张桌子。然后你再想,在总共(A+B-2) 群建筑中选(A-1) 群放到最高建筑的左边,不就有(C_{A+B-2}^{A-1}) 种方案吗!所以总方案是(C_{A+B-2}^{A-1}*S_{n-1}^{A+B-2})
优秀的(O(1))询问。
(C)和(S)预处理一下就珂以辣!
你问我什么是斯特林数?出门转百度or组合数学其实是我懒得写了
上代码:
#include<bits/stdc++.h>
#define mod 1000000007
using namespace std;
int T,n,a,b;
long long s[50002][202],c[102][202];//要开long long别问我怎么知道的
inline int rd(){//辣鸡快读,大佬勿喷
int ans=0,flag=1;
char ch=getchar();
while((ch<'0'||ch>'9')&&ch!='-')ch=getchar();
if(ch=='-')flag=-1,ch=getchar();
while(ch>='0'&&ch<='9')ans=ans*10+ch-48,ch=getchar();
return ans*flag;
}
int main(){
T=rd();
for(register int i=0;i<=200;i++){
c[i][0]=1;
}
for(register int i=1;i<=200;i++){
for(register int j=1;j<=i;j++){
c[i][j]=(c[i-1][j-1]+c[i-1][j])%mod;//记得取模
}
}
memset(s,0,sizeof(s));
s[0][0]=1;
for(register int i=1;i<=5e4;i++){
for(register int j=1;j<=200;j++){
s[i][j]=(s[i-1][j-1]%mod+s[i-1][j]*(i-1)%mod)%mod;
}
}
while(T--){
n=rd(),a=rd(),b=rd();
printf("%lld
",(c[a+b-2][a-1]*s[n-1][a+b-2])%mod);
}
return 0;
}
切黑题,啦啦啦