poj 3068 Bridge Across Islands

Bridge Across Islands

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 11196		Accepted: 3292		Special Judge

Description

Thousands of thousands years ago there was a small kingdom located in the middle of the Pacific Ocean. The territory of the kingdom consists two separated islands. Due to the impact of the ocean current, the shapes of both the islands became convex polygons. The king of the kingdom wanted to establish a bridge to connect the two islands. To minimize the cost, the king asked you, the bishop, to find the minimal distance between the boundaries of the two islands.

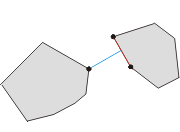
Input

The input consists of several test cases.
Each test case begins with two integers N, M. (3 ≤ N, M ≤ 10000)
Each of the next N lines contains a pair of coordinates, which describes the position of a vertex in one convex polygon.
Each of the next M lines contains a pair of coordinates, which describes the position of a vertex in the other convex polygon.
A line with N = M = 0 indicates the end of input.
The coordinates are within the range [-10000, 10000].

Output

For each test case output the minimal distance. An error within 0.001 is acceptable.

Sample Input

4 4
0.00000 0.00000
0.00000 1.00000
1.00000 1.00000
1.00000 0.00000
2.00000 0.00000
2.00000 1.00000
3.00000 1.00000
3.00000 0.00000
0 0

Sample Output

1.00000

题意：求两个凸包之间的最近距离
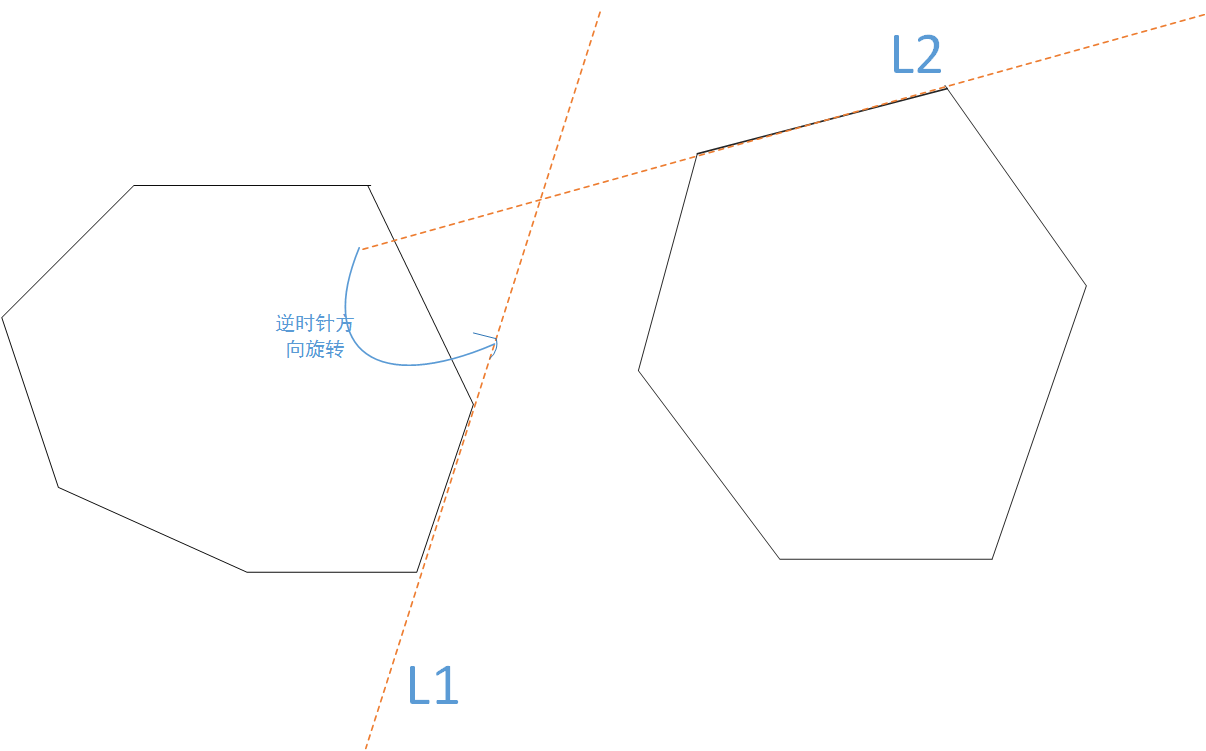
思路：找到第一个凸包的右下角的顶点和第二个凸包左上角的顶点,第一个凸包从右下角顶点开始与逆时针方向的下一个顶点作直线，暂且固定这条直线，第二个凸包的左上角的顶点也与逆时针方向下一个顶点结合作直线，判断两条直线方向，若第二条直线需要逆时针转动才能转到第一条直线的方向，那么第二条直线继续逆时针旋转，即
逆时针方向找到接下来一个顶点，这个顶点与上一个顶点形成新的直线，直到当前形成的直线与第一条直线平行或者需要顺时针旋转才能转到第一条直线的方向为止停止转动,并计算当前的两条直线所在的线段的距离，更新最短距离。之后第一条直线逆时针转动到下一个方向后继续固定，重复上述算法。。

AC代码：

Source Code

Problem: 3608        User: ach11090913
Memory: 980K        Time: 172MS
Language: C++        Result: Accepted
Source Code
#define _CRT_SECURE_NO_DEPRECATE
#include<iostream>
#include<algorithm>
#include<vector>
#include<set>
#include<cmath>
using namespace std;
#define EPS 1e-10
#define INF 0x3f3f3f3f
const int N_MAX = 10000*2+16;
double add(double a,double b) {
    if (abs(a + b) < EPS*(abs(a) + abs(b)))return 0;
    return a + b;
}

struct P {
    double x, y;
    P(){}
    P(double x,double y):x(x),y(y) {}
    P operator +(P p) {
        return P(add(x, p.x), add(y, p.y));
    }
    P operator -(P p) {
        return P(add(x, -p.x), add(y, -p.y));
    }
    P operator *(P p) {
        return P(x*p.x, y*p.y);
    }
    bool operator <(const P& p)const {
        if (x != p.x)return x < p.x;
        else return y < p.y;
    }
    double dot(P p) {
        return add(x*p.x,y*p.y);
    }
    double det(P p) {
        return add(x*p.y, -y*p.x);
    }
    double norm() {
        return x*x + y*y;
    }
    double abs() {
        return sqrt(norm());
    }

};
bool cmp_y1(const P&p,const P&q) {
    if (p.y != q.y)
    return p.y < q.y;
    return p.x > q.x;
}

struct Segment {
    P p1, p2;
    Segment(P p1=P(),P p2=P()):p1(p1),p2(p2) {}
};
typedef Segment Line;
typedef vector<P>Polygon;

inline double cross(P A, P B, P C)
{
    return (B - A).det(C - A);
}



double getDistanceLP(Line l,P p) {
    return fabs((l.p2 - l.p1).det(p - l.p1)) / ((l.p2 - l.p1).abs());
}

double getDistanceSP(Segment s,P p) {
    if ((s.p2 - s.p1).dot(p - s.p1) < 0.0)return (p - s.p1).abs();
    if ((s.p1 - s.p2).dot(p - s.p2) < 0.0)return (p - s.p2).abs();
    return getDistanceLP(s, p);
}

double getDistance(Segment s1,Segment s2) {
    return min(min(getDistanceSP(s1,s2.p1),getDistanceSP(s1,s2.p2)),
        min(getDistanceSP(s2,s1.p1),getDistanceSP(s2,s1.p2)));
}

Polygon po1, po2;
int N, M;

vector<P> judge_clockwise(vector<P>p) {
    for (int i = 0; i < p.size()-2;i++) {
        //double tmp = (p[i + 1] - p[i]).det(p[i + 2] - p[i + 1]);
        double tmp = cross(p[i], p[i + 1], p[i + 2]);
        if (tmp > EPS)return p;
        else if (tmp < -EPS) {
            reverse(p.begin(), p.end());
            return p;
        }
    }
    return p;
}


double solve() {
    int i = 0, j = 0;
       for (int k = 0; k < N;k++) {
           if (!cmp_y1(po1[i], po1[k]))i = k;//i为凸包右下角
        }
       for (int k = 0; k < M; k++) {
           if (cmp_y1(po2[j], po2[k]))j = k;//j为凸包左上角
       }
       double res = INF;
       for (int k = 0; k< N;k++) {
           while ((po1[i] - po1[(i + 1) % N]).det(po2[(j + 1) % M] - po2[j]) < 0) j = (j + 1) % M;
           Segment s1, s2;
           s1.p1 = po1[i], s1.p2 = po1[(i + 1) % N],s2.p1=po2[j],s2.p2=po2[(j+1)%M];
           res = min(res, getDistance(s1, s2));
          //cout << s1.p1.x << " " << s1.p1.y << " " << s1.p2.x << " " << s1.p2.y <<" " << s2.p1.x << " " << s2.p1.y << " " << s2.p2.x <<" "<< s2.p2.y << endl;
           i = (i + 1) % N;
       }
       return res;
}

int main() {
    
    while (scanf("%d%d",&N,&M)&&N) {
        po1.clear();
        po2.clear();
        for (int i = 0; i < N;i++) {
            double x, y;
            scanf("%lf%lf",&x,&y);
            po1.push_back(P(x,y));
        }
        po1=judge_clockwise(po1);
        for (int i = 0; i < M;i++) {
            double x, y;
            scanf("%lf%lf", &x, &y);
            po2.push_back(P(x,y));
        }
        po2=judge_clockwise(po2);
        printf("%.5f
",solve());
    }
    return 0;
}