Description
现在有一棵二叉树,所有非叶子节点都有两个孩子。在每个叶子节点上有一个权值(有n个叶子节点,满足这些权值为1..n的一个排列)。可以任意交换每个非叶子节点的左右孩子。
要求进行一系列交换,使得最终所有叶子节点的权值按照遍历序写出来,逆序对个数最少。
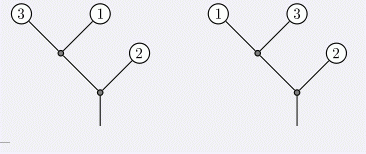
Solution
WA了好久。。这题怎么造数据拍啊喂TvT
后来发现数组开小了,越界(叶子结点是n个,然而还有很多非叶子节点)
dfs的时候自底向上线段树合并,一边合并左右子树一边计算出左右子树放在前面时对对方产生的逆序对数量,取较小的一种
#include<iostream> #include<cstdio> #include<cstring> #include<cstdlib> #define MAXN 400005 typedef long long LL; using namespace std; int n,root,tot1=0,tot2=0; int v[MAXN],ch[MAXN][2],rt[MAXN],ls[MAXN*10],rs[MAXN*10],sum[MAXN*10]; LL ans=0,cnt1,cnt2; int read() { int x=0,f=1;char c=getchar(); while(c<'0'||c>'9'){ if(c=='-')f=-1;c=getchar(); } while(c>='0'&&c<='9'){ x=x*10+c-'0';c=getchar(); } return x*f; } void build(int &idx,int l,int r,int x) { tot2++,idx=tot2; sum[idx]++; if(l==r)return; int mid=(l+r)>>1; if(x<=mid)build(ls[idx],l,mid,x); else build(rs[idx],mid+1,r,x); } int merge(int x,int y) { if(!x||!y)return x+y; cnt1+=(LL)sum[ls[x]]*sum[rs[y]]; cnt2+=(LL)sum[rs[x]]*sum[ls[y]]; sum[x]=sum[x]+sum[y]; ls[x]=merge(ls[x],ls[y]); rs[x]=merge(rs[x],rs[y]); return x; } void dfs(int &k) { tot1++,k=tot1; v[k]=read(); if(v[k])build(rt[k],1,n,v[k]); else { dfs(ch[k][0]),dfs(ch[k][1]); cnt1=cnt2=0; rt[k]=merge(rt[ch[k][0]],rt[ch[k][1]]); ans+=min(cnt1,cnt2); } } int main() { n=read(); dfs(root); printf("%lld ",ans); return 0; }