摘要：数字水印在保护多媒体数字产品版权方面发挥着巨大作用, 是信息隐藏领域研究的热点之一, 数字水印算法对不可感知性和鲁棒性要求较高, 变换域DCT技术能更好地满足水印的不可感知性和鲁棒性。本文对基于DCT变换的数字水印算法进行阐述,并通过Matlab进行模拟。
关键词：数字水印；DCT变换；鲁棒性；算法模拟
1 前言
随着数字技术的发展，Internet应用日益广泛，数字媒体因其数字特征极易被复制、篡改、非法传播及蓄意攻击，其版权保护已日益引起人们的关注。因此，研究新形势下行之有效的版权保护和认证技术具有深远的理论意义和广泛的应用价值。
数字水印技术，是指在数字化的数据内容中嵌入不明显的记号，从而达到版权保护或认证的目的。被嵌入的记号通常是不可及或不可察觉的，但是通过一些计算操作可以被检测或提取。因此，数字图像的内嵌水印必须具有以下特点：透明性、鲁棒性、安全性。
在图像的DCT系数上嵌入水印信息具有诸多优势，首先，DCT变换是实数域变换，对实系数的处理更加方便，且不会使相应的信息发生改变。第二，DCT变换是有损图像压缩JPEG的核心，基于DCT变换的图像水印将兼容JPEG图像压缩。最后，图像的频域系数反应了能量分布，DCT变换后图像能量集中在图像的低频部分，即DCT图像中不为0的系数大部分集中在一起（左上角），因此编码效率很高，将水印信息嵌入图像中频系数上具有较好的鲁棒性。
2 相关算法
2.1 水印嵌入算法
水印嵌入算法是通过调整载体图像子块的中频DCT系数的大小来实现对水印信息的编码嵌入。
算法描述如下：
读取原始载体图像A，对A进行8*8分块，并对每块图像进行DCT变换，在8*8的子块中，中频系数的掩模矩阵取为
每个子块的中频系数总共有11个位置。每个子块的中频位置可以嵌入11个像素点的亮度值，对应地，将水印图像按照11个像素点一组进行分块，水印图像的最后一个分块如果不足11个像素点，则通过把亮度值置0进行扩充。
对载体图像DCT系数进行修改，有 
，i=1,...,11 ，其中 是载体图像中频系数的DCT值， 是变换后的DCT值， 
为水印嵌入的强度，这里取 
，
为对应位置的水印图像的灰度值（或亮度值）。
对修改后的DCT矩阵进行DCT逆变换，得到嵌入了水印的合成图像。
2.2 水印提取算法
水印提取是水印嵌入的逆过程，具体算法描述如下
（1）计算合成图像和原始载体图像的差图像
。
（2）对差图像
进行8*8分块，并对每个小块做DCT变换。
（3）从DCT小块中提取可能的水印序列 
，
用下列函数计算可能的水印 和原嵌入水印 的相关性：
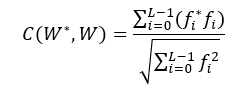
式中，
和 
分别为图像W 和 W*的灰度值（或亮度值），L为像素点的个数。
根据相似性的值就可以判断图像中是否含有水印，从而达到版权保护的目的。判定准则为，事先设定一个阈值T ，若 
，可以判定被测图像中含有水印，否则没有水印。
3 仿真实验
通过Matlab R2014a进行仿真实验
3.1 读取文件
以图1中图像作为载体图像原图，图2中图像作为水印图像原水印，图1为256*256像素8位深度的bmp格式图像，图2为50*50像素8位深度的bmp格式图像
图1 原图
图2 原水印
代码如下：
a=imread('原图.bmp'); %读入载体图像,图像的长和高都必须化成8的整数倍 [M1,N1]=size(a); %计算载体图像的大小 a=im2double(a); %数据转换成double类型 knum1=M1/8; knum2=N1/8; %把载体图像划分成8×8的子块，高和长方向划分的块数 b0=imread('原水印.bmp'); %读入水印图像 b=im2double(b0); %数据转换成double类型 subplot(1,2,1), imshow(a) %显示载体图像 subplot(1,2,2), imshow(b) %显示水印图像
3.2 插入水印
根据2.1水印嵌入算法，选择嵌入强度因子为 ，代码如下
mask1=[1 1 1 1 0 0 0 0 1 1 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]; %给出低频的掩膜矩阵 ind1=find(mask1==1); %低频系数的位置 mask2=[0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]; %给出中频的掩膜矩阵 ind2=find(mask2==1); %中频系数的位置，总共11个 [M2,N2]=size(b); %计算水印图像的大小 L=M2*N2; %计算水印图像的像素个数 knum3=ceil(M2*N2/11); %水印图像按照11个元素1块，分的块数 b=b(:); b(L+1:11*knum3)=0; %水印图像数据变成列向量，后面不足一块的元素补0 T=dctmtx(8); %给出8×8的DCT变换矩阵 ab=zeros(M1,N1); %合成图像的初始值 k=0; %嵌入水印块计数器的初始值 for i=0:knum1-1 %该两层循环进行水印嵌入 for j=0:knum2-1 xa=a([8*i+1:8*i+8],[8*j+1:8*j+8]); %提取载体图像的子块 ya=T*xa*T'; %载体图像子块做DCT变换 coef1=(mask1+mask2).*ya; %提取低频和中频系数，作为合成子块的初始值 if k<knum3 coef1(ind2)=coef1(ind2)+0.05*b(11*k+1:11*k+11); %在中频系数上嵌入水印子块的信息 end ab([8*i+1:8*i+8],[8*j+1:8*j+8])=T'*coef1*T; %对合成子块进行逆DCT变换 k=k+1; end end
3.3 提取水印
根据2.2水印提取算法，代码如下
acha=ab-a; %提取合成图像和原图像的差图像； k=0; tb=zeros(11*knum3,1); %提取水印图像的初始值 for i=0:knum1-1 %该两层循环进行水印提取 for j=0:knum2-1 xa2=acha([8*i+1:8*i+8],[8*j+1:8*j+8]); %提取差图像的子块 ya2=T*xa2*T'; %差图像子块做DCT变换 coef2=mask2.*ya2; %提取差图像中频DCT系数 if k<knum3 tb(11*k+1:11*k+11)=20*coef2(ind2); %提取水印图像的像素值 end k=k+1; end end tb(L+1:end)=[]; %把水印图像列向量的后面补的0删除 tb=reshape(tb,[M2,N2]); %把列向量变成矩阵 figure, subplot(1,1,1), imshow(ab) %显示水印合成图像 figure, subplot(1,1,1), imshow(tb) %显示提取的水印图像 imwrite(ab,'处理后的图.bmp','bmp') imwrite(tb,'提取的水印.bmp','bmp')
4 实验结果讨论
4.1 实验结果
根据3仿真实验，原图像和原水印为图3左一，嵌入水印后的合成图像为图3左二，提取的水印图像图3左三。图4为实验文件。
图3 实验结果
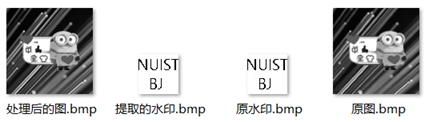
图4 实验文件
4.2 不同嵌入强度因子测试
实验选取0和0.01到0.09不同嵌入强度因子进行测试，测试结果如下：
表1 不同嵌入强度因子测试结果
| α |
提取的水印和添加水印的图像 |
视觉效果 |
|
0 |
 |
无提取水印 图像清楚 |
|
0.01 |
 |
无明显提取水印 图像清楚 |
|
0.02 |
 |
提取水印可见 图像清楚 |
|
0.03 |
 |
提取水印可见 图像清楚 |
|
0.04 |
 |
提取水印可见 图像清楚 |
|
0.05 |
 |
提取水印与原水印接近 图像清楚 |
|
0.06 |
 |
提取水印与原水印接近 图像清楚 |
|
0.07 |
 |
提取水印与原水印接近 图像稍微影响 |
|
0.08 |
 |
提取水印与原水印接近 图像稍微影响 |
|
0.09 |
 |
提取水印与原水印接近 图像有影响 |
5 总结
数字水印是信息隐藏领域研究热点之一，本文通过对图片数字水印中基于DCT变换的水印算法模拟，通过对8位bmp灰度的测试，对该算法处理图像的不可感知性和鲁棒性有了初步的认识。其中嵌入强度因子测试的选取尤为重要，本次模拟结论是嵌入强度因子测试为0.05有较好的效果，提取水印与原水印接近，图像清楚，在实际生产生活中可通过预设阈值，根据检测相似性的值判断图像中是否含有水印，从而达到版权保护的目的，在选择阈值时，既要考虑误检也要考虑虚警。
参考文献：
[1]成宇. 基于DCT和最佳的嵌入强度因子的数字水印算法的研究[D].天津工业大学,2017.
[2]张春玉.基于DCT变换的数字水印算法研究[J].河北农机,2019(01):71-72.
[3]陈小娥.基于DCT变换的数字水印算法研究[J].长春工程学院学报(自然科学版),2018,19(03):98-101.
[4]王琳娟,李君霞.基于分块的多级DCT和SVD的鲁棒水印算法[J].计算机时代,2017(09):51-55.
[5]wiki.《离散余弦变换》.
https://zh.wikipedia.org/wiki/BMP.2019年5月20访问
[6]wiki.《离散余弦变换》.
https://zh.wikipedia.org/wiki/%E7%A6%BB%E6%95%A3%E4%BD%99%E5%BC%A6%E5%8F%98%E6%8D%A2.2019年5月20访问
