1谓词
1.1引入
在研究命题逻辑中,原子命题是命题演算中最基本的单位,不再对原子命题进行分解,这样会产生两大缺点:
(1)不能研究命题内部的结构,成分和内部逻辑的特征;
(2)也不可能表达两个原子命题所具有的共同特征,甚至在命题逻辑中无法处理一些简单又常见的推理过程。
例如 著名的“苏格拉底三段论”:
凡人都是要死的,
苏格拉底是人,
所以苏格拉底是要死的。
显然,该论证是正确的,但不能用命题逻辑的推理规则推导出来。
1.2定义
我们可将原子命题分解成两部分:个体(名词,代词)+ 谓词(动词)。
例如: 人总是要死的
![]() 是无理数。
是无理数。
小王比小明高。
在命题的研究中,基于谓词分析的逻辑,称为谓词逻辑。谓词逻辑是命题逻辑的扩充和发展。
谓词逻辑 (对原子命题分割)
1.3谓词的概念与表示法
简单命题中表示主体或客体的词,称为个体。通常用a,b,c,…表示。
用以刻画客体的性质或关系的模式,称为谓词。通常用大写字母 F,G,H,…表示。
例如 张华是大学生。李明是大学生。
若 G:表示“是学生”,a:表示“张华”,b:表示“李明”.
则上述两个命题可符号化为: G(a)与G(b).
例如 小王比小明高。
若 H:表示“…比…高”; a:表示“小王”, b:表示“小明”.
则上述命题可符号化为:H(a,b).绝不可以写为:H(b, a).
1′谓词填式:谓词字母后填以客体所得的式子。 例如: G(a) 、G(b)、H(a, b)
2′若谓词字母联系着一个客体,则称作一元谓词;
若谓词字母联系着二个客体,则称作二元谓词;
若谓词字母联系着n个客体,则称作n元谓词。
一元谓词表示一个个体所具有的性质;
n 元谓词表示n个个体之间的关系。
3′客体的次序必须是有规定的。
1.4命题函数
1.4.1定义
例如 F:“总是要死的。”
a:“张华”; a:“老虎” ; c:“桌子”;
则 F(a),F(b), F(c)均为命题。
在上例中,若令 x 表示个体变元, x ɛ {a,b,c},则 F(x):x 总是要死的.称F(x)为命题函数。 (变化的命题)
1.4.2简单命题函数
定义:由一个谓词字母F和一个非空的个体变元集合D所组成的表达式,称为简单命题函数。
分析:
a)当简单命题函数仅有一个个体变元时,称为一元简单命题函数;
当命题函数含有两个个体变元时,则称为二元简单命题函数。
b)用任何个体去取代客体变元之后,则命题函数就变为命题;
c)命题函数中个体变元的取值范围称为个体域(论述域)。
例如:F(x) : x 是质数。 (一元命题函数)
G(x , y): x 生于 y。(二元命题函数)
其值取决于个体域。
个体域的给定形式有二种:
①具体给定。 eg:{a, b, c}
②全总个体域:宇宙间的一切事物组成的个体域。所有的个体都从该域中取得。
1.4.3命题函数化为命题
将命题函数化为命题,通常有两种方法:
1)将 x 取定一个值。 如:F(4),F(5).
2)将谓词量化。 如:∀ x F(x), ∃ x F(x).
例如:任何正整数都大于零。——命题
可表示为 ∀x F(x).
谓词与函数的比较
|
代数 |
自变量 |
函数 |
函数值 |
定义域 |
|
逻辑 |
个体变元 |
谓词 |
命题 |
个体域 |
2量词
2.1定义
对个体变元数量限制的词,称为量词。


2.2全称量词
例如 “这里所有的东西都是苹果”
可写成: ∀x A(x)或(∀x) A(x).
“∀”几种表达式的读法:
∀ x P(x): “对所有的x,x 是…”;
∀ x ¬ P(x) : “对所有x,x 不是…”;
¬∀ x P(x) : “并不是对所有的x,x 是…”;
¬∀ x ¬ P(x) : “并不是所有的x,x 不是…”。
例如:将“对于所有的 x 和任何的 y,如果 x高于 y,那么 y 不高于 x”写成命题表达形式。
解: ∀ x ∀ y (G(x , y) → ¬G(y , x))
G(x , y):x 高于 y.
2.3存在量词
“∃”几种表达式的读法:
∃ x P(x): “存在一个 x,使 x 是…”;
∃ x ¬ P(x) : “存在一个 x,使 x 不是…”;
¬ ∃ x P(x) : “不存在一个 x,使 x 是…”;
¬ ∃ x ¬ P(x) : “不存在一个 x,使 x 不是…”。
例如:(a)存在一个人;
(b)某个人很聪明;
(c)某些实数是有理数
将(a),(b),(c)写成命题。
解:规定:M(x):x 是人;C(x):x 是很聪明;
R1(x):x 是实数(特性谓词);
R2(x):x 是有理数;
则 (a) ∃ x M(x) ;
(b) ∃ x (M(x) ∧ C(x));
(c) ∃ x (R1(x) ∧ R2(x)) 。
2.4真值与否定
量化命题的真值:决定于给定的个体域.
例如 给定个体域:{a1,…,an}。
以{a1,…,an}中的每一个个体代入
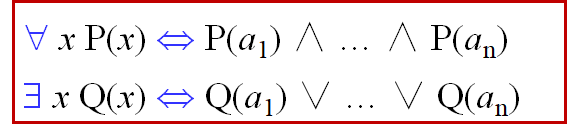
量词与否定联结词“¬”之间的关系:
例:设P(x)表示x今天来校上课, 比较可以得到:
¬(∀x)P(x) ⇔ (∃ x)¬ P(x)
¬( ∃ x)P(x) ⇔ (∀x)¬ P(x)
3谓词公式
3.1定义
不出现命题联结词和量词的谓词命名式称为原子谓词公式,并用P(x1,…,xn)来表示。
(P为 n 元谓词, x1,…,xn为个体变元),当n=0 时称为零元谓词公式。
谓词公式的归纳法定义:
⑴原子谓词公式是谓词公式;
⑵若A是谓词公式,则¬A也是谓词公式;
⑶若A, B都是谓词公式,则(A∧B),(A∨B) ,(A→B)和(A↔B)都是谓词公式;
⑷若A是谓词公式,x 是任何变元,则
∀ x A, ∃ x A也都是谓词公式;
⑸只有按⑴—⑷所生成得的那些公式才是谓词公式(谓词公式又简称“公式”)。
例如 将下列命题翻译成谓词公式。
(1) 凡偶数均能被2整除。
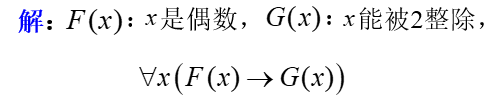
(2) 存在着偶素数。
![]()
(3) 没有不犯错误的人。
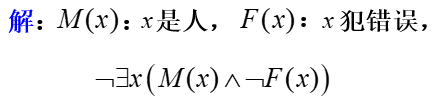
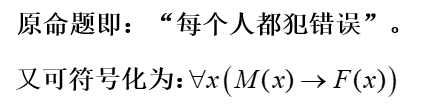
(4) 在北京工作的人未必是北京人。

(5) 尽管有些人聪明,但未必一切人都聪明。
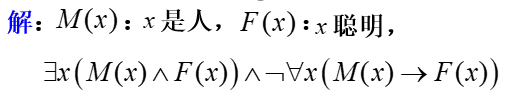
(6) 每列火车都比某些汽车快。
某些汽车比所有的火车慢。

3.2量词使用注意
使用量词时,应注意以下5点:
(1) 在不同个体域中,命题符号化的形式可能不一样;
(2) 一般,除非有特别说明,均以全总个体域为个体域;
(3)n元谓词化为命题至少需要n个量词,
(4)多个命题变元出现时,不能随意颠倒顺序,否则命题的含义完全改变。
(5) 在引入特性谓词 M(x)时,M(x)以蕴含前件加在“∀”后,以合取项加在“∃”后。即,
对全称量词“∀”,用“ M(x)→? ”加入;
对存在量词“∃”,用“ M(x)∧ ?”加入。
例1:将下面命题符号化。
(1) 所有的有理数均可表成分数。
(2) 有的有理数是整数。

例2:任何整数或是正的,或是负的。

例3:试将苏格拉底论证符号化:“所有的人总是要死的。因为苏格拉底是人,所以苏格拉底是要死的。”

3.3 变元的约束
3.3.1定义
辖域:紧接在量词后面括号内的谓词公式。
例如 ∀x P(x) ,∃ x (P(x) ∧ Q(x)) 。
若量词后括号内为原子谓词公式,则括号可以省去。
约束变元:在量词的辖域内,且与量词下标相同的变元。
自由变元:当且仅当不受量词的约束。
例如: ∀x P(x , y) , ∀x(P(x)→∃ y(P(x , y)) 。
3.3.2约束变元的改名规则
在谓词公式中,约束变元的符号是可以更改的。
例如:
![]()
下面介绍约束变元的改名规则:
(a)若要改名,则该变元在量词及其辖域内的所有出现均需一起更改;
(b)改名时所用的变元符号必须是量词辖域内未曾出现的符号。
例如:公式 ∀x P(x)→∃ y P(x , y) 可改写成
∀x P(x)→∃ z P(x , z) ,
但不能改成:∀x P(x)→∃ x P(x , x) ,
∃ x P(x , x)中前面的x原为自由变元,现在变为约束变元了。
3.3.3区别是命题还是命题函数的方法
(a)若在谓词公式中出现有自由变元,则该公式为命题函数;
(b)若在谓词公式中的变元均为约束出现,则该公式为命题。
例如: ∀x P(x, y, z)是二元谓词,
∃ y ∀x P(x, y, z)是一元谓词,
∀x P(x)是命题
即谓词公式中如果没有自由变元出现,则该公式是一个命题。
例1:“没有不犯错的人。”
解:设 F(x) 为“x犯错误”,
M(x) 为“x是人”(特性谓词)。
可把此命题写成:
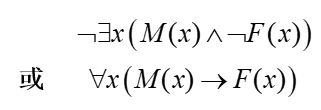
例2: “x 是 z 的父亲且 z 是 y 的母亲”。
解:设P(z):z是人;
F(x , z):x是z的父亲;
M(z , y):z是y的母亲。
则谓词公式可写成:
![]()
且该命题函数表示“x 是 y 的外祖父”。
3.4个体域
(1)个体域不同,则表示同一命题的谓词公式的形式不同。
例如:“所有的人都是要死的。”
令D(x):x是要死的。
下面给出不同的个体域来讨论:
(ⅰ)个体域为:{人类},
则可写成 ∀x D(x) ;
(ⅱ)个体域为任意域(全总个体域),则人必须首先从任意域中分离出来.
设M(x):x是人,(M(x)为特性谓词)。
命题可写成∀x(M(x) → D(x)).
(2) 个体域不同,则表示同一命题的值不同。
|
设 Q(x): x<5 |
{-1,0,3} |
{-3,6,2} |
{15,30} |
|
∀ x Q(x) |
T |
F |
F |
|
∃ x Q(x) |
T |
T |
F |
(3)对于同一个体域,用不同的量词时,特性谓词加入的方法不同。
对于全称量词,其特性谓词以前件的方式加入;
对于存在量词,其特性谓词以与的形式加入。
(4)量词对变元的约束,往往与量词的次序有关。
例如:∀y ∃x (x < y-2))表示任何 y 均有 x, 使得x < y-2。
4谓词演算的永真公式
4.1定义
A,B为两个谓词公式,E为它们的共同个体域,
若对A和B的任一组变元进行赋值,都有A和B的值相同,
则称A和B遍及E是互为等价的,记为A ⇔ B.
给定谓词公式A,E是A的个体域。
若给A中个体变元指派E中的每一个个体所得命题的值均为真,
则称A在E中是永真的。
若E为任意域则称A是永真的。
给定谓词公式A,E是A的个体域。
若给A中个体变元指派E中每一个个体,在E中存在一些个体名称,使得指派后的真值为“T”,则A称是可满足的。
若给A中个体变元指派个体域中的任一个体,命题的值均为“F”,则称A是永假的。
4.2谓词公式的永真式
4.2.1不含量词的谓词公式的永真式
只要用原子谓词公式去替换命题公式的永真式中的原子命题变元,则在第一章中永真蕴含式和等价公式均可变成谓词演算中的永真式:


4.2.2 含有量词的等价式和永真蕴含式
设个体域为:S={a1,a2,…,an},我们有: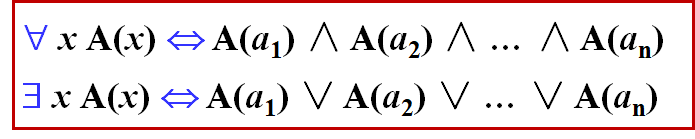
说明:
若个体域是有限的,则可省掉量词。
若个体域是无限的,则可将上述概念推广从而省去量词,不过要注意这是由无限项组成的命题。
例如:设个体域为:N={0,1,2…},A(x):x>3 ,则可写出:
∀ x A(x) ⇔ A(0) ∧ A(1) ∧ A(2)∧ …
∃ x A(x) ⇔ A(0) ∨ A(1) ∨ A(2) ∨ …
证明:设个体域为: S={a1,a2,…,an}.
¬ ∃ x P(x) ⇔ ¬(P(a1) ∨ P(a2) ∨ … ∨ P(an))
⇔ ¬ P(a1) ∧ ¬ P(a2) ∧ … ∧ ¬ P(an)
⇔ ∀ x ¬P(x)
下面举例说明量化命题和非量化命题的差别:否定形式不同
例如: 否定下列命题:
(a)上海是一个小城镇 A(s)
(b)每一个自然数都是偶数 ∀ x (N(x) → E(x))
上述二命题的否定为:
(a)上海不是一个小城镇 ¬ A(s)
(b)有一些自然数不是偶数
¬ ∀ x (N(x) → E(x))
(b)有一些自然数不是偶数
¬ ∀ x (N(x) → E(x)) ⇔ ∃ x ¬ (N(x) → E(x))
⇔ ∃ x ¬ (¬ N(x)∨E(x))
⇔ ∃ x (N(x)∧¬ E(x))
结论:对于非量化命题的否定只需将动词否定,而对于量化命题的否定不但对动词进行否定,而且对量词同时进行否定,其方法是:
∀ x 的否定变为∃ x , ∃ x 的否定变为∀ x 。


证明:设个体域为: S={a1,a2,…,an}.
∀x A(x)∨P
⇔ (A(a1) ∧ A(a2) ∧ … ∧ A(an) )∨ P
⇔ (A(a1) ∨ P) ∧ … ∧ (A(an) ∨ P)
⇔ ∀ x(A(x) ∨ P )
证明:设个体域为: S={a1,a2,…,an}.
∃ x(A(x) → B )
⇔ (A(a1) → B) ∨ … ∨ (A(an) → B)
⇔ (¬ A(a1) ∨ B) ∨ … ∨ (¬ A(an) ∨ B)
⇔ (¬ A(a1) ∨ … ∨ ¬ A(an)) ∨ B
⇔ ∃ x ¬ A(x) ∨ B
⇔ ¬ ∀x A(x) ∨ B
⇔ ∀ x A(x) → B 
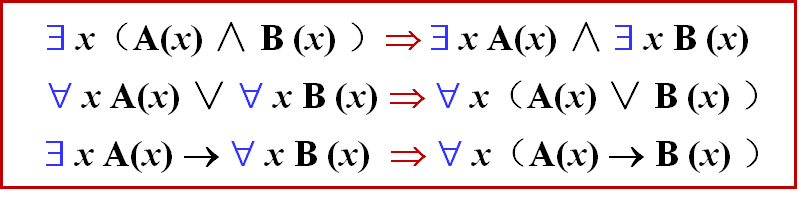
证明:设个体域为: S={a1,a2,…,an}.
1. ∀ x(A(x) ∧ B (x) )
⇔ (A(a1)∧B (a1) ) ∧ … ∧ (A(an)∧B (an) )
⇔ (A(a1)∧ … ∧A(an)) ∧ (B(a1)∧ … ∧B(an))
⇔ ∀ x A(x) ∧ ∀ x B (x)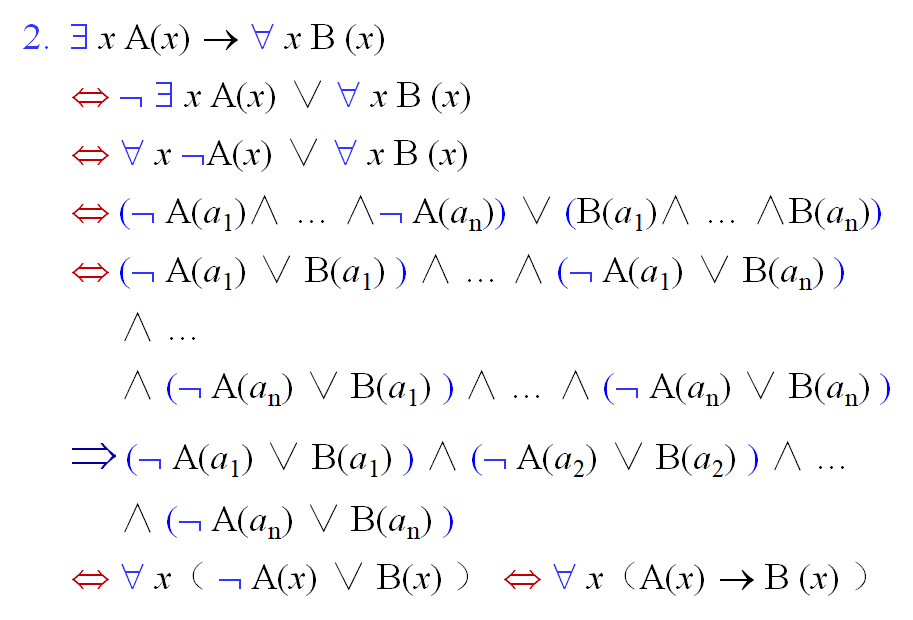




下面列出对应的表达式可以看出其不同处:
设 x 的个体域为: {a1, a2, …, an} ,
y 的个体域为: {b1, b2, …, bn} ,
则:
(1) ∀x ∃y P(x , y)
⇔ ∃y P(a1 , y) ∧ … ∧ ∃y P(an , y)
⇔ (P(a1 , b1) ∨ … ∨ P(a1 , bn) )∧ … ∧(P(an , b1) ∨ … ∨ P(an , bn) )
(2) ∃y ∀x P(x , y)
⇔ ∀x P(x , b1) ∨ … ∨ ∀x P(x , bn)
⇔ (P(a1 , b1) ∧ … ∧ P(an , b1) ) ∨ … ∨ (P(a1 , bn) ∧ … ∧ P(an , bn) )
例如:x , y的个体域{鞋子},
P(x , y) :x 和 y 配成一双鞋子。
则
∀x ∃y P(x , y) ⇔ T
∃y ∀x P(x , y) ⇔ F
例如:x , y 的个体域为 N={0,1,2…},则
∀x ∀y P(x , y)
⇔ ∀y P(0, y) ∧∀y P(1, y) ∧∀y P(2, y) ∧ …
⇔ (P(0, 0) ∧P(0, 1) ∧ … ∧ P(0, j) ∧ …)
∧… ∧
(P(i, 0) ∧P(i, 1) ∧ … ∧ P(i , j) ∧ …)
∧…
⇔ (P(0, 0) ∧P(1, 0) ∧ … ∧ P(i , 0) ∧ …)
(P(0, 1) ∧P(1, 1) ∧ … ∧ P(i , 1) ∧ …)
∧…
⇔ ∀x P(x, 0) ∧∀ x P(x, 1) ∧ … ∧ ∀ x P(x, j) ∧ …
⇔∀y ∀x P(x , y)
同样: ∃ x ∃ y P(x , y) ⇔∃ y ∃x P(x , y) 
例如 ¬ ∀ x ∃ y ∀ z P(x , y , z)
⇔ ∃ x ¬ ∃ y∀ z P(x , y , z)
⇔ ∃ x ∀ y ¬ ∀ z P(x , y , z)
⇔ ∃ x∀ y ∃ z ¬ P(x , y , z) 
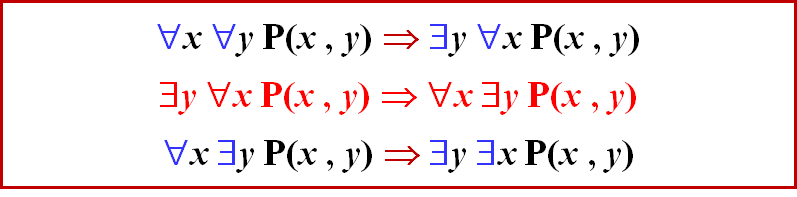
![]()


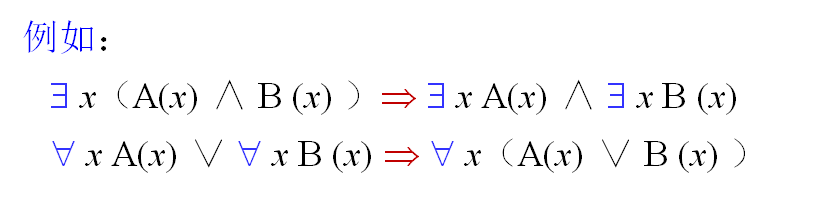
4.3前束范式
4.3.1定义
定义:一个公式,如果量词均非否定地在全式的开头,它们的作用域延伸到整个公式的末尾,则称此公式叫前束范式
例如: ∀x ∃ y ∀z (¬ Q(x , y) ∨ R(z))
(前束范式)
定理:任何一个谓词公式均和一个前束范式等价。
证明:
①利用量词转换把 ¬ 深入到原子谓词公式前;
②利用约束变元的改名规则;
③利用量词辖域的扩张收缩律,把量词移到全式的最前面,这样一定可得到等价的前束范式。
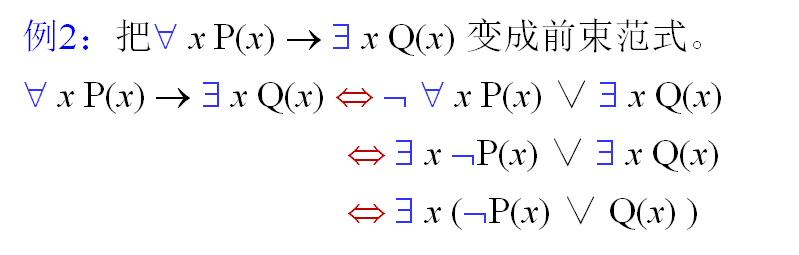
5谓词演算的推理规则
5.1 含有量词的特殊永真式
设A(x)是一个谓词公式,x 是其中的自由变元,
若把 y 代入到A(x)里而不会产生变元新的约束出现,则称A(x)对于 y 是自由的。
例如:①下面A(x)对于 y 是自由的:
A(x) ⇔ ∀z P(z) ∧ Q(x , z),这里 x 为自由变元,若用 y 去取代A(x)中的x,
A(y) ⇔ ∀z P(z) ∧ Q(y , z),这里 y 也为自由变元.
例如:②下面A(x)对于 y 不是自由的:
A(x) ⇔ ∀y (S(x) → S(y)),这里 x 为自由变元,若用 y 去取代A(x)中的x,
A(y) ⇔ ∀y (S(y) → S(y)),这里 y 变为约束变元了,产生了新的约束出现.
如果必须要代入 y,则应先将A(x)中的约束变元 y 改名,即
A(x) ⇔ ∀z (S(x) → S(z)),
然后用 y 去取代A(x)中的x,得
∀z (S(y) → S(z)),y 仍为自由变元.
总结: 判定A(x)对于 y是自由的,只要看公式A(x)中∀y ,∃ y的辖域内有没有 x 的自由出现就行:
若有 x 的自由出现,则A(x)对于 y 不是自由的,若无 x 的自由出现,则一定可以肯定A(x)对于 y 是自由的。
5.2四个推理规则





5.3推理规则使用说明
5.3.1命题逻辑中
命题逻辑中的P规则,T规则,CP规则和间接证明法,都可以引用到谓词逻辑的推理规则中来,
不过要注意对量词做适当处理
其方法是:可用US,ES在推导中去掉量词;可用UG,EG使结论量化。
5.3.2四个推理规则
四个推理规则的使用说明:
(1)在使用ES,US时,一定要是前束范式;
(2)推导中连续使用US规则时,可用相同变元
∀x P(x) ⇒ P(y)
∀x Q(x) ⇒ Q(y)
(3)推导中若既用ES,又用US, 则必须先用ES ,后用US,方可取相同变元,反之不行。
∃ x P(x) ⇒ P(y)
∀x Q(x) ⇒ Q(y)
(4)推导中连续使用ES规则时,使用一次更改一个变元。
例1:证明苏格拉底三段论:“凡人都是要死的,苏格拉底是人,所以苏格拉底是要死的。”
证明:设 F(x):x是人;
G(x):x是要死的;
a:苏格拉底
于是命题可化为: ![]()

例2 证明 ∀x (H(x) → M(x)) ,∃x H(x) ⇒ ∃x M(x)
例3 证明 ∃x (P(x) → Q(x)) ⇒ ∀x P(x) → ∃x Q(x)

例4 证明
¬ ∀x ( P(x) ∧ Q(x) ) ,∀x P(x) ⇒ ¬ ∀x Q(x)
例5 下列结论能否从前提中推出:
∀x ( P(x) → Q(x) ) ,¬ Q(c) ⇒ ∀x ¬P(x)
注意:在使用US,ES,UG,EG这四条规则时,要严格按照它们的规定去使用。
5.3.3 二个量词的推理
构造下面定理的证明: ![]()