1、循环链表
我们之前说过了单链表,大家应该都有印象吧,那么循环链表是什么呢?
循环链表就是将单链表中终端结点的指针端自空指针改为指向头结点,就使整个单链表形成一个环,这种头尾相接的单链表称为单循环链表,简称循环链表 (circular linked list) 。
那么循环链表出现的目的是为什么呢?
循环链表解决如何从当中一个结点出发,访问到链表的全部结点。
为了使空链表与非空链表处理一致,我们通常设一个头结点,当然,这并不是说,循环链表一定要头结点,这需要注意。 结构图如下:

其实循环链表与单链表主要差异主要体现在循环的判断条件上,单链表判断最后一个节点的指针域是否为空,而循环链表判断最后一个节点的指针域是否为头节点。
操作代码可以参考我之前做的单链表的代码,只是在添加尾节点的时候将尾节点的指针域为空,改为指向头指针。
2、双向链表
终于到了最后一个链表结构了,双向链表,那么双向链表又是什么呢?
双向链表 (double linked List) 是在单链表的每个结点中,再设置一个指向其前驱结点的指针域。所以在双向链表中的结点都有两个指针域, 一个指向直接后继,另一个指向直接前驱。
那么为什么我们要设置这种链表结构呢?
主要是为了解决单链表,查找下一节点的时间复杂度为O(1),但是查找上一节点的时间复杂度为O(n)的问题,也就是为了解决单链表的单一性查找的问题。
双向链表可以是循环链表,也可以不是循环链表,但是我们一般还是用循环双向链表偏多,毕竟使用起来比较方便。结构图如下:
双向链表是单链表中扩展出来的结构,所以它的很多操作是和单链表相同的,比如求长度的 ListLength ,查找元素的 GetElem,获得元素位置的 LocateElem 等,这些操作都只要涉及一个方向的指针即可,另一指针多了也不能提供什么帮助。
双向链表既然是比单链表多了如可以反向遍历查找等数据结构,那么也就需要付出一些小的代价:在插入和删除时,需要更改两个指针变化。
插入操作时其实并不复杂,不过顺序很重要,如图所示:

千万不要写反了,如果先执行4,再执行其他的,找不到后继的位置,那么插入就会失败,
删除节点稍微简单点,如图所示:

操作代码如下:
public class DoubleLinkList<T> {
private Node<T> headPoint;// 定义头节点
private Node<T> tail;// 定义尾节点
/**
* 定义一个节点类
*
* @author 紫薇天钺
*
* @param <T>
*/
private static class Node<T> {
T data;// 泛型数据
Node<T> next;// 构建指针域,指向下一个节点
Node<T> prev;// 构建指针域,指向上一个节点
Node(T data) {// 节点的构造函数
this.data = data;
}
}
/**
* 添加头节点
*/
public void addHeadPoint() {
this.headPoint = new Node<T>(null);// 创建一个空值节点赋值给头节点
}
/**
* 添加尾节点
*/
public void addTail(T data) {
this.tail = new Node<T>(data);// 创建一个节点赋值给尾节点
this.tail.prev = headPoint;// 尾节点的前驱指针域指向头节点
this.tail.next = headPoint;// 尾节点的后继指针域指向头节点
this.headPoint.next = tail;// 头节点的后继指针指向尾节点
this.headPoint.prev = tail;// 头节点的前驱域指向尾节点
}
/**
* 使用头部插入法添加节点
*/
public void insertNode(T data) {
if (this.headPoint == null) {// 如果头节点为空,添加头节点
addHeadPoint();
}
if (this.tail == null) {// 如果尾节点为空,添加尾节点
addTail(data);
}
Node<T> newNode = new Node<T>(data);// 创建一个新的节点
newNode.prev = this.headPoint;// 新节点的前驱域指向头节点
newNode.next = this.headPoint.next;// 新节点的后继域指向下一个节点
headPoint.next.prev = newNode;// 新节点的后继节点的前驱域指向新节点
headPoint.next = newNode;// 头节点的后继域指向新节点
}
/**
* 在指定位置添加节点
*
* @param index
* @param node
* @throws Exception
*/
public void insertNodeByIndex(int index, Node<T> node) throws Exception {
if (index < 0 || index >= length()) {// 判断新插入的位置是否正确
throw new Exception("插入的位置不合法");
}
int length = 1;// 定义我们遍历的长度
Node<T> temp = headPoint.next;// 从头节点下一个节点开始遍历
while (temp != null) {// 如果链表不为空,并且插入的位置不在头节点之前
if (index == length++) {// 到达指定位置,这里到达的位置为插入位置的前一个节点
node.next = temp.next;// 将新节点的后继域指向插入位置的前一个节点下一个节点
node.prev = temp;// 将新节点的前驱域指向插入位置的前一个节点
temp.next.prev = node;// 将插入位置的前一个节点的下一个节点前驱域指向新节点
temp.next = node;// 将插入位置的前一个节点后继域指向新节点
return;
}
temp = temp.next;
}
}
/**
* 根据节点位置删除节点
*
* @param index
* @throws Exception
*/
public void deleteNodeByIndex(int index) throws Exception {
if (isEmpty()) {// 判断链表是否为空
throw new Exception("链表为空,不能删除");
}
if (index < 0 || index >= length()) {// 判断删除的位置是否正确
throw new Exception("删除的位置不合法");
}
int length = 1;// 开始遍历的位置
Node<T> temp = headPoint.next;// 循环节点
while (temp != null) {// 如果链表不为空,并且删除的位置不在头节点之前
if (index == length++) {// 到达指定位置,这里到达的位置为删除位置的前一个节点
temp.next = temp.next.next;
temp.next.prev = temp;
return;
}
temp = temp.next;
}
}
/**
* 判断链表是否为空
*
* @return
*/
public Boolean isEmpty() {
return this.headPoint == null;
}
/**
* 获取链表的长度
*
* @return
*/
public int length() {
int length = 0;
Node<T> temp = headPoint;
while (temp.next != headPoint) {
length++;
temp = temp.next;
}
return length;
}
/**
* 获取节点的值
*
* @param i
* @return
*/
public T getValue(int i) {
Node<T> node = headPoint.next;
int j = 0;
while (node != null && j < i) {
node = node.next;
j++;
}
return node.data;
}
/**
* 测试
*
* @param ages
* @throws Exception
*/
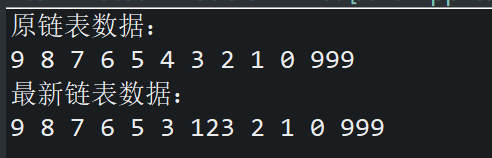
public static void main(String ages[]) throws Exception {
DoubleLinkList<Integer> list = new DoubleLinkList<Integer>();
list.addHeadPoint();
list.addTail(999);
for (int j = 0; j < 10; j++) {
list.insertNode(j);
}
System.out.println("原链表数据:");
for (int k = 0; k < list.length(); k++) {
System.out.print(list.getValue(k) + " ");
}
list.insertNodeByIndex(7, new Node<Integer>(123));
list.deleteNodeByIndex(5);
System.out.println();
System.out.println("最新链表数据:");
for (int k = 0; k < list.length(); k++) {
System.out.print(list.getValue(k) + " ");
}
}
}
最终运行结果如下:
3、链表的总结回顾
线性表终于结束了,我们先谈了它的定义,线性表是零个或多个具有相同类型的数据元素的有限序列。然后谈了线性表的抽象数据类型,如它的一些基本操作。
之后我们就线性表的两大结构做了讲述,先讲的是比较容易的顺序存储结构,指的是用一段地址连续的存储单元依次存储线性表的数据元素。通常我们都是用数组来实现这一结构。
后来是我们的重点,由顺序存储结构的插入和删除操作不方便,引出了链式存储结构。它具有不受固定的存储空间限制,可以比较快捷的插入和删除操作的特点。然后我们分别就链式存储结构的不同形式,如单链表、循环链表和双向链表做了讲解。
总体示意图如下:
