[SHOI2012]回家的路

题目背景

SHOI2012 D2T1

题目描述

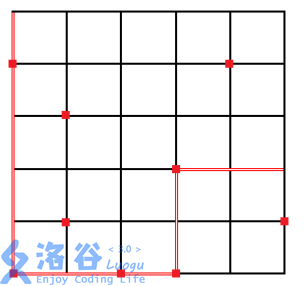
2046 年 OI 城的城市轨道交通建设终于全部竣工，由于前期规划周密，建成后的轨道交通网络由2n2n条地铁线路构成，组成了一个nn纵nn横的交通网。如下图所示，这2n2n条线路每条线路都包含nn个车站，而每个车站都在一组纵横线路的交汇处。

出于建设成本的考虑，并非每个车站都能够进行站内换乘，能够进行站内换乘的地铁站共有mm个，在下图中，标上方块标记的车站为换乘车站。已知地铁运行 1 站需要 2 分钟，而站内换乘需要步行 1 分钟。Serenade 想要知道，在不中途出站的前提下，他从学校回家最快需要多少时间（等车时间忽略不计）。

输入输出格式

输入格式：

第一行有两个整数n,mn,m。

接下去mm行每行两个整数x,yx,y,表示第xx条横向线路与第yy条纵向线路的交

汇站是站内换乘站。

接下去一行是四个整数x_1,y_1,x_2,y_2x1,y1,x2,y2。表示 Serenade 从学校回家时，在第 x_1x1条横向线路与第y_1y1条纵向线路的交汇站上车，在第x_2x2条横向线路与第y_2y2条纵向线路的交汇站下车。

输出格式：

输出文件只有一行，即 Serenade 在合理选择线路的情况下，回家所需要的时间。如果 Serenade 无法在不出站换乘的情况下回家，请输出-1。

说明

对于 30%的数据，nle 50,mle 1000n≤50,m≤1000；

对于 60%的数据，nle 500,mle 2000n≤500,m≤2000；

对于 100%的数据，nle 20000,mle 100000n≤20000,m≤100000；

---

对于每行每列暴力连边显然是要炸的

考虑只把相邻的点间连边，对于同行同列是没有影响的

然鹅转向就跪了

经过一番深思熟虑，我们可以把每个点拆开啊

对于每个点，横向建一个点，纵向建一个点，把这两个点间连边(edge=1)

然后最短路就行了

---

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
#define M 1000000
#define LL long long
#define max(a,b) ((a)>(b)? (a):(b))
#define min(a,b) ((a)<(b)? (a):(b))
#define abs(a) ((a)>0? (a) :-(a))
using namespace std;
queue<int> q;
int i,m,n,j,k,ver[M],edge[M],head[M],nex[M],cnt,pre[M],sx,sy,ex,ey,b[M],d[M];

struct vv
{
	int x,y,w;
} a[M];

void add(int x,int y,int z)
{
	cnt+=1;
	ver[cnt]=y, nex[cnt]=head[x], head[x]=cnt, edge[cnt]=z;
}

bool cmpx(vv a,vv b){return a.x==b.x? a.y<b.y : a.x<b.x;}
bool cmpy(vv a,vv b){return a.y==b.y? a.x<b.x : a.y<b.y;}

void spfa()
{
	memset(d,0x3f,sizeof(d));
	d[0]=b[0]=1;
	q.push(0);
	while(q.size())
	{
		int r=q.front(); q.pop();
		b[r]=0;
		for(int i=head[r];i;i=nex[i])
		{
			int t=ver[i]; 
			if(d[r]+edge[i]<d[t]) 
			{
				d[t]=d[r]+edge[i];
				if(!b[t]) q.push(t);
				b[t]=1;
			}
		}
	}
}

int main()
{
	scanf("%d%d",&n,&m);
	for(i=1;i<=m;i++) scanf("%d%d",&a[i].x,&a[i].y), a[i].w=i;
	scanf("%d%d%d%d",&sx,&sy,&ex,&ey);
	sort(a+1,a+1+m,cmpx);
	for(i=2;i<=m;i++)
	{
		if(a[i].x==a[i-1].x)  add(i,i-1,(a[i].y-a[i-1].y)*2), add(i-1,i,(a[i].y-a[i-1].y)*2);
		if(a[i].x==sx) add(0,i,abs(a[i].y-sy)*2);
		if(a[i].x==ex) add(i,m+1+m,abs(a[i].y-ey)*2);
	}
	
	sort(a+1,a+1+m,cmpy);
	for(i=2;i<=m;i++)
	{
		if(a[i].x==a[i-1].x)  add(i+m,i-1+m,(a[i].x-a[i-1].x)*2), add(i-1+m,i+m,(a[i].x-a[i-1].x)*2);
		if(a[i].y==sy) add(0,i+m,abs(a[i].x-sx)*2);
		if(a[i].y==ey) add(i+m,m+1+m,abs(a[i].x-ex)*2);
	}
	
	for(i=1;i<=m;i++) add(i,i+m,1), add(i+m,i,1);
	spfa();
	printf("%d",d[m+m+1]);
}