最大子矩形

极大子矩阵

一个(n*m)的矩阵中有(s)个位置是障碍，问最大的不包含障碍的矩形面积
最大子矩形问题-王知坤 （对于这篇论文.....吐槽无力

虽然实现..至少它的思路很对嘛

枚举所有的极大子矩形找出最大子矩形(s^2)

悲惨经历：找到一份题解，学学学学学学学。WA了。{改改改改改改改...WA了（此处循环1w次}，然后气愤的测题解，WA了........

每个极大子矩形的每一条边外侧一定有至少一个障碍或与边界重合，不然将边向外移即可获得更大子矩形，不满足极大。因此只需要按(y)排好序后依次枚举每个障碍作为左端点，然后向右找每一个点作为右端点，向上向下找出此时的上边界和下边界即找到了一个极大子矩形。
考虑实现找上下边界的方法

1.先把边界设为上下界，找到第一个点设为右边界

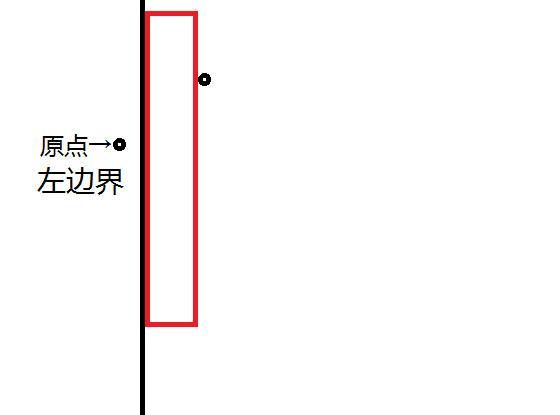
2.比较这个点，若在原点和上界间的话将其设为上界，在原点和下界间的话设为下界，与原点同行的话break即可
3.再看下一个点，反复即可

   	  #include<iostream>
#include<stdio.h>
#include<cmath>
#include<algorithm>
using namespace std;

int i,m,n,j,k,ans,b[5001][5001];
char c;
struct vv
{
   int x,y;
} a[1000001];

bool cmp1(vv a,vv b) {return a.x<b.x;}
bool cmp2(vv a,vv b) {return a.y<b.y;}
bool cmp3(vv a,vv b) {return a.y>b.y;}

void dfs()
{
   for(int i=1;i<k;i++)
   {
   	int maxx=n, minn=1;
   	for(int j=i+1;j<=k;j++)
   	{
   		if(a[j].y==a[i].y) continue; 
   		ans=max(ans,(abs(a[j].y-a[i].y)-1)*(maxx-minn+1));
   		if((a[j].x<=a[i].x)&&(a[j].x+1>minn)) minn=a[j].x+1;
   		if((a[j].x>=a[i].x)&&(a[j].x-1<maxx)) maxx=a[j].x-1;
   		if(-minn+maxx+1<=0) break;
   	}
   }
}

int main()
{
   scanf("%d%d%d",&n,&m);
   for(i=1;i<=n;i++)
   	for(j=1;j<=m;j++)
   	{
   		scanf("%d",&j);
   		if(j) a[++k].x=i,a[k].y=j;
   	}

   a[++k].x=0; a[k].y=0;  a[++k].x=0; a[k].y=m+1;
   a[++k].x=n+1; a[k].y=0;  a[++k].x=n+1; a[k].y=m+1;
   sort(a+1,a+1+k,cmp1);
   for(i=2;i<=k;i++) ans=max(ans,(a[i].x-a[i-1].x-1)*m);
   sort(a+1,a+1+k,cmp2);  dfs();
   sort(a+1,a+1+k,cmp3);  dfs();
   printf("%d",ans);
}

由于有时障碍可能非常密集，这个方法就会被卡掉

悬线(O(nm))

由于极大子矩阵的上边界上方一定有一个障碍，所以找出每一个点上方的最近障碍点即构成一条悬线
然后把这条悬线左右移动直到遇到障碍及构成了一个极大子矩形。
枚举每一个点，只要能够(O(1))的间找到其为下端对应悬线和向左右能够移动距离即可在(O(nm))的时间中找到答案。
考虑预处理方法
1. 悬线长度(h[i][j]) 如果(i,j)上方的点是障碍， (h[i][j]=1)，否则(h[i][j]=h[i-1][j])
2. 左右移动距离,向左移动最大距离(l[i][j]=max()当前行左边最近障碍坐标(+1,l[i-1][j])),右移道理相通
3. 特殊情况：(i,j)上方的点是障碍时(l[i][j]=)当前行左边最近障碍坐标(+1)
最后(ans=max(ans,h[i][j]*(r[i][j]-l[i][j]+1)))

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;

int i,m,n,j,k,a[5001][5001],b[5001][5001],l[5001][5001],r[5001][5001],g,h,ans,las;
char c;
int main()
{
    scanf("%d%d%d",&n,&m);
    for(i=1;i<=n;i++)
        for(j=1;j<=m;j++)
            scanf("%d",a[i][j]);

    for(i=1;i<=n;i++)
        for(j=1;j<=m;j++)
            if(!a[i][j]) b[i][j]=b[i-1][j]+1;
                if(a[i-1][j]) b[i][j]=1;

    for(i=1;i<=n;i++)
    {
        las=1;
        for(j=1;j<=m;j++)
        {
            if(a[i-1][j]) l[i][j]=las;
            else l[i][j]=max(l[i-1][j],las);	
            if(a[i][j]) las=j+1;	
        }
    }

    for(i=1;i<=m;i++) r[0][i]=m;
    for(i=1;i<=n;i++)
    {
        las=m;
        for(j=m;j>=1;j--)
        {
            if(a[i-1][j]) r[i][j]=las;
            else r[i][j]=min(r[i-1][j],las);
            if(a[i][j]) las=j-1;
        }
    }
            
    for(i=1;i<=n;i++)
        for(j=1;j<=m;j++)
            if(!a[i][j]) ans=max(ans,3*(b[i][j])*(r[i][j]-l[i][j]+1));
    printf("%d",ans);
}