将每一个两两相乘的最优先记录好
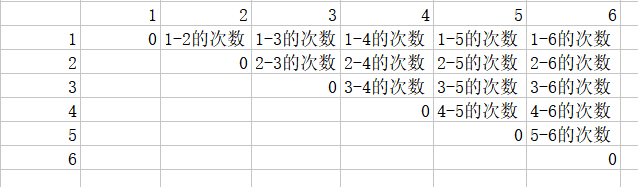
先计算出小的区间的最优,于是可以推出大的区间的最优。以下是求解的顺序,先把1-2、2-3等等相差为1的计算出答案,
然后求1-3、 2-4等等相差为2的最优答案,以此类推,右上角的格子为问题的解。
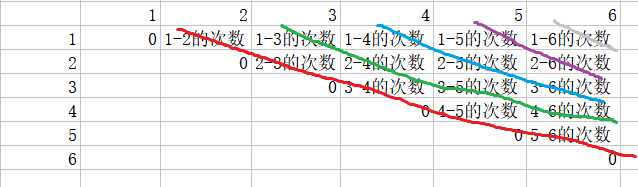
2-5(即:2、 3、 4、 5)这个区间,可由2-3与3-5构成,还能由2-4与4-5构成,有下图。
看看实例.
算法设计例题:矩阵连乘(DP)
- Time Limit: 1000/500 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
- Total Submission(s): 1618 Accepted Submission(s): 545
Description
给定n个矩阵{ A1,A2,…,An },保证Ai与Ai+1是可乘的,i = 1,2,…,n-1。考察这n个矩阵的连乘积A1A2…An。由于矩阵乘法满足结合律,故计算矩阵的连乘积可以有许多不同的计算次序。这种计算次序可以用加括号的方式来确定。现要求设计一个高效的算法,对给定的n个矩阵确定一个计算次序使得总的乘法次数最少,并输出该最优值。
Input
输入的第一行是单独一个整数T,表示案例的数目。每个案例的第一行是单独一个n ( 1 ≤ n≤ 50 ),表示矩阵的个数。接下来第n行,依序分别对应第i个矩阵,每行包括两个整数xi,yi(1 ≤ i ≤ n,1 ≤ xi , yi ≤ 100 ),表示该矩阵的行数和列数。保证n个矩阵依序是可乘的。
Output
每个案例输出一个整数,表示最少需要的乘法次数。
Sample Input
1
4
50 10
10 40
40 30
30 5
Sample Output
10500
1 #include<cstdio> 2 using namespace std; 3 const int maxn=60; 4 int dp[maxn][maxn],a[maxn];///a记录每个行列 5 6 int main() 7 { 8 int n,T; 9 while( ~scanf("%d",&T)){ 10 while( T--){ 11 scanf("%d",&n); 12 for(int i=1;i<=n;i++){ 13 dp[i][i]=0; 14 scanf("%d%d",&a[i-1],&a[i]); 15 ///因为前一个的列等于后一个的行,所以可以进行覆盖 16 } 17 18 int temp; 19 for(int num=2;num<=n;num++){ ///次数 20 for(int i=1;i<=n-num+1;i++){ 21 int j=i+num-1; ///前一个的位置 22 dp[i][j]=dp[i+1][j]+a[i-1]*a[i]*a[j]; ///按顺序计算的解。 23 for(int k=i+1;k<=j-1;k++){ 24 temp=dp[i][k]+dp[k+1][j]+a[i-1]*a[k]*a[j]; 25 ///区间解 26 if(dp[i][j]>temp) 27 dp[i][j]=temp; 28 } 29 } 30 } 31 printf("%d ",dp[1][n]); 32 } 33 } 34 return 0; 35 }