Buy or Build
| Time Limit: 2000MS | Memory Limit: 65536K | |
| Total Submissions: 1369 | Accepted: 542 |
Description
World Wide Networks (WWN) is a leading company that operates large telecommunication networks. WWN would like to setup a new network in Borduria, a nice country that recently managed to get rid of its military dictator Kurvi-Tasch and which is now seeking for investments of international companies (for a complete description of Borduria, have a look to the following Tintin albums ``King Ottokar's Sceptre", ``The Calculus Affair" and ``Tintin and the Picaros"). You are requested to help WWN todecide how to setup its network for a minimal total cost.
Problem
There are several local companies running small networks (called subnetworks in the following) that partially cover the n largest cities of Borduria. WWN would like to setup a network that connects all n cities. To achieve this, it can either build edges between cities from scratch or it can buy one or several subnetworks from local companies. You are requested to help WWN to decide how to setup its network for a minimal total cost.
You have to decide which existing networks you buy and which edges you setup so that the total cost is minimal. Note that the number of existing networks is always very small (typically smaller than 8).
A 115 Cities Instance
Consider a 115 cities instance of the problem with 4 subnetworks (the 4 first graphs in Figure 1). As mentioned earlier the exact shape of a subnetwork is not relevant still, to keep figures easy to read, we have assumed an arbitrary tree like structure for each subnetworks. The bottom network in Figure 1 corresponds to the solution in which the first and the third networks have been bought. Thin edges correspond to edges build from scratch while thick edges are those from one of the initial networks.
Problem
There are several local companies running small networks (called subnetworks in the following) that partially cover the n largest cities of Borduria. WWN would like to setup a network that connects all n cities. To achieve this, it can either build edges between cities from scratch or it can buy one or several subnetworks from local companies. You are requested to help WWN to decide how to setup its network for a minimal total cost.
- All n cities are located by their two-dimensional Cartesian coordinates.
- There are q existing subnetworks. If q>=1 then each subnetwork c ( 1<=c<=q ) is defined by a set of interconnected cities (the exact shape of a subnetwork is not relevant to our problem).
- A subnetwork c can be bought for a total cost wc and it cannot be split (i.e., the network cannot be fractioned).
- To connect two cities that are not connected through the subnetworks bought, WWN has to build an edge whose cost is exactly the square of the Euclidean distance between the cities.
You have to decide which existing networks you buy and which edges you setup so that the total cost is minimal. Note that the number of existing networks is always very small (typically smaller than 8).
A 115 Cities Instance
Consider a 115 cities instance of the problem with 4 subnetworks (the 4 first graphs in Figure 1). As mentioned earlier the exact shape of a subnetwork is not relevant still, to keep figures easy to read, we have assumed an arbitrary tree like structure for each subnetworks. The bottom network in Figure 1 corresponds to the solution in which the first and the third networks have been bought. Thin edges correspond to edges build from scratch while thick edges are those from one of the initial networks.
Input
The
first line contains the number n of cities in the country (
1<=n<=1000 ) followed by the number q of existing subnetworks (
0<=q<=8 ). Cities are identified by a unique integer value ranging
from 1 to n . The first line is followed by q lines (one per
subnetwork), all of them following the same pattern: The first integer
is the number of cities in the subnetwork. The second integer is the the
cost of the subnetwork (not greater than 2 x 106 ). The
remaining integers on the line (as many as the number of cities in the
subnetwork) are the identifiers of the cities in the subnetwork. The
last part of the file contains n lines that provide the coordinates of
the cities (city 1 on the first line, city 2 on the second one, etc).
Each line is made of 2 integer values (ranging from 0 to 3000)
corresponding to the integer coordinates of the city.
Output
Your program has to write the optimal total cost to interconnect all cities.
Sample Input
7 3 2 4 1 2 3 3 3 6 7 3 9 2 4 5 0 2 4 0 2 0 4 2 1 3 0 5 4 4
Sample Output
17
Hint
Sample Explanation: The above instance is shown in Figure 2. An optimal solution is described in Figure 3 (thick edges come from an existing network while thin edges have been setup from scratch).
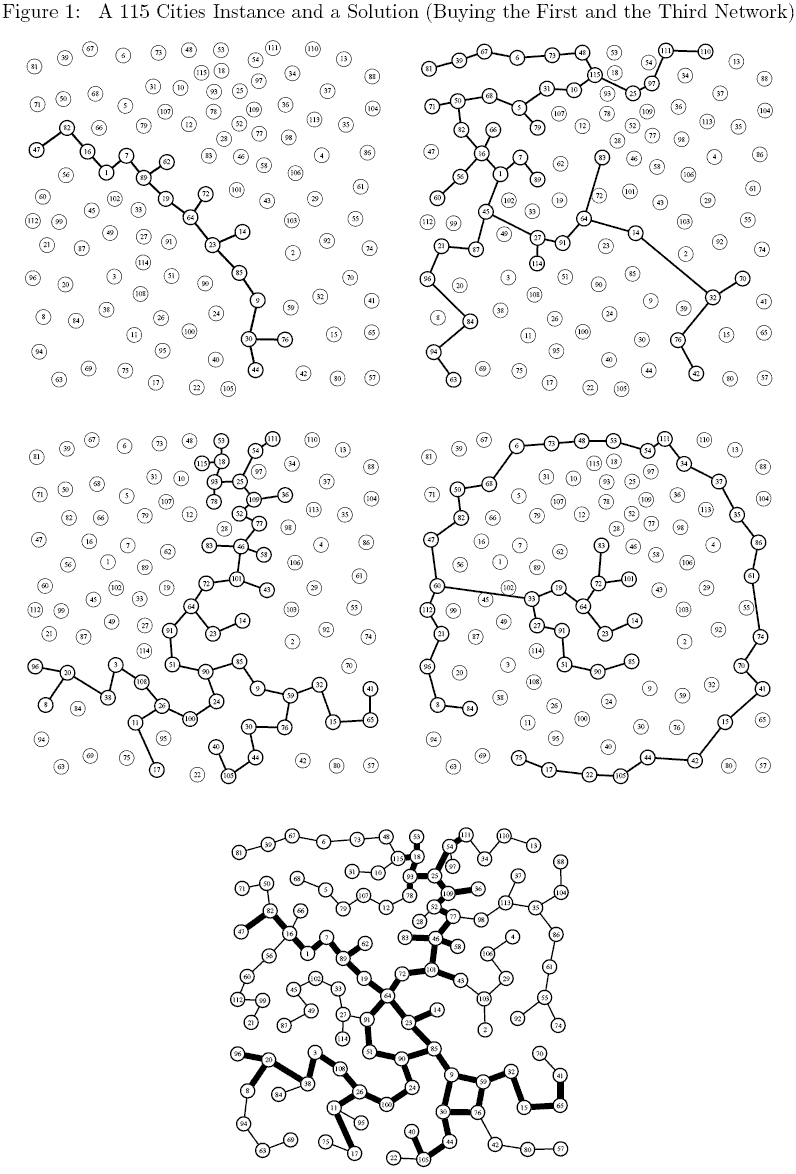
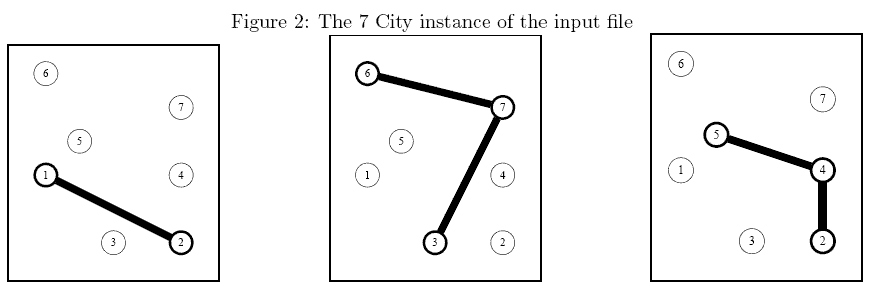
Figure 3: An optimal solution of the 7 City instance in which which the first and second existing networkshave been bought while two extra edges (1, 5) and (2, 4)
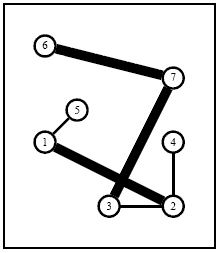


Figure 3: An optimal solution of the 7 City instance in which which the first and second existing networkshave been bought while two extra edges (1, 5) and (2, 4)

Source
题意:使n个城市全部连同所需要的最低花费。其中可以购买方案来代替修建。
知识点:图论,最小生成树,状态压缩,枚举。
思路:1.“n个城市”,"连通",“最低花费",可以想到最小生成树。按每条边的权值(权值是一个统称,在这里指的的是距离长短)排序,然后用Kruskal算法得到最小生成树。2.由于方案数q小于8,数字很小考虑到状态压缩,2的q次方种情况一一枚举得到最小值。(PS:在上述1中可以得到所有方案都不购买的情况)。
1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <algorithm> 5 #include<cmath> 6 #include<sstream> 7 #include<string> 8 using namespace std; 9 #define M 10000 10 int t,n,m,k,num; 11 int root[10005]; 12 struct Node 13 { 14 int x; 15 int y; 16 };//city corrdinate(城市坐标) 17 Node node[1005]; 18 struct Buy 19 { 20 int a[10005]; 21 int cost; 22 int k; 23 };//project(方案) 24 Buy buy[10005]; 25 int vis[10005]; 26 struct Edage 27 { 28 int u; 29 int v; 30 int len; 31 bool operator<(const Edage &a)const //自定义小于号用于边的排序。 32 { 33 return len<a.len; 34 } 35 }; 36 Edage edage[1000005]; 37 int cal(int a,int b) 38 { 39 int dis=(node[a].x-node[b].x)*(node[a].x-node[b].x)+(node[a].y-node[b].y)*(node[a].y-node[b].y); 40 return dis; 41 } 42 void add_edage(int a,int b) 43 { 44 edage[num].u=a; 45 edage[num].v=b; 46 edage[num].len=cal(a,b); 47 num++; 48 }//建边 49 void init() 50 { 51 for(int i=1;i<=n;i++) 52 root[i]=i; 53 } 54 int fi(int x) 55 { 56 int k,j,r; 57 r=x; 58 while(r!=root[r]) 59 r=root[r]; 60 k=x; 61 while(k!=r) 62 { 63 j=root[k]; 64 root[k]=r; 65 k=j; 66 } 67 return r; 68 } 69 void uni(int a,int b) 70 { 71 int x=fi(a); 72 int y=fi(b); 73 if(x!=y) 74 root[x]=y; 75 76 } 77 int kruskal() 78 { 79 int ans=0; 80 int cnt=0; 81 for(int i=0;i<num;i++) 82 { 83 int x=fi(edage[i].u); 84 int y=fi(edage[i].v); 85 if(x!=y) 86 { 87 root[x]=y; 88 ans+=edage[i].len; 89 cnt++;} 90 if(cnt==n-1) 91 break; 92 } 93 return ans; 94 } 95 void solve() 96 { 97 init(); 98 int ans=kruskal(); 99 //int all=0; 100 for(int i=0;i<(1<<m);i++)//状态压缩 101 { 102 init(); 103 int all=0; 104 for(int j=0;j<m;j++) 105 { 106 if(i&(1<<j))//取方案 107 continue; 108 for(int k=0;k<buy[j].k-1;k++) 109 uni(buy[j].a[k],buy[j].a[k+1]); 110 all+=buy[j].cost; 111 } 112 ans=min(ans,all+kruskal());//保存最小花费 113 } 114 printf("%d ",ans); 115 } 116 int main() 117 { 118 scanf("%d",&t); 119 while(t--) 120 { 121 num=0; 122 memset(vis,0,sizeof(vis)); 123 scanf("%d%d",&n,&m); 124 for(int i=0;i<m;i++) 125 { 126 scanf("%d%d",&buy[i].k,&buy[i].cost); 127 for(int j=0;j<buy[i].k;j++) 128 scanf("%d",&buy[i].a[j]); 129 } 130 for(int i=1;i<=n;i++) 131 scanf("%d%d",&node[i].x,&node[i].y); 132 133 for(int i=1;i<=n;i++) 134 for(int j=i+1;j<=n;j++) 135 add_edage(i,j); 136 sort(edage,edage+num); 137 solve(); 138 if (t) puts(""); 139 140 } 141 142 return 0; 143 } 144 //1 145 // 146 //7 3 147 //2 4 1 2 148 //3 3 3 6 7 149 //3 9 2 4 5 150 //0 2 151 //4 0 152 //2 0 153 //4 2 154 //1 3 155 //0 5 156 //4 4