2-15 矩阵基础2

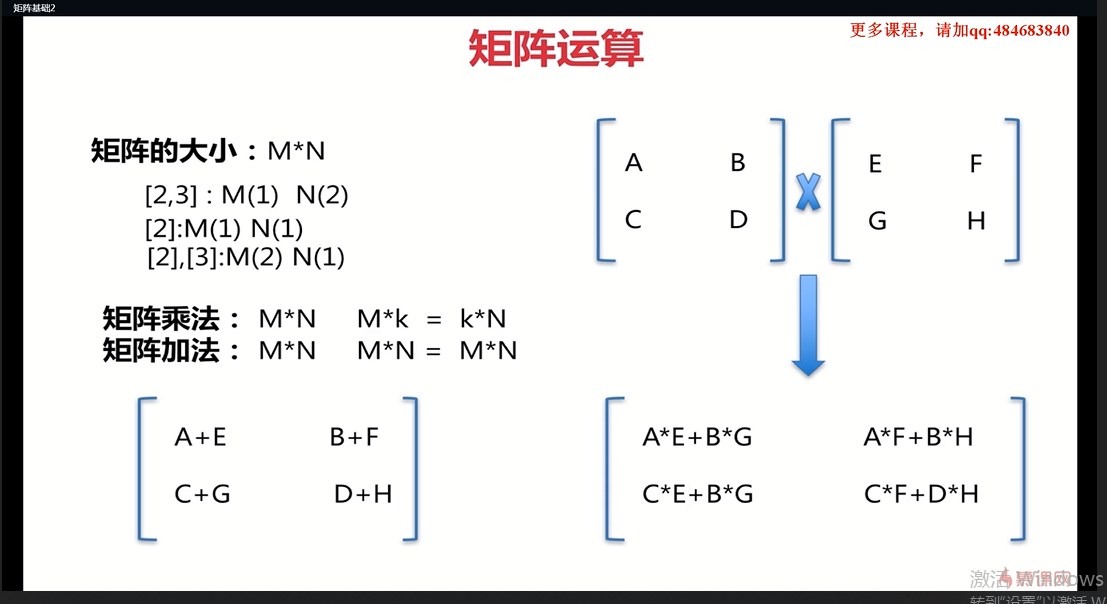
一种矩阵加法，两种矩阵乘法。矩阵加法非常简单，就是对应元素的相加。第一个矩阵是M行k列，第二个矩阵必须是k行N列。第一个矩阵的列必须要和第二个矩阵的行数相同。这样它们乘出来的结果就是M*N。第一个的列和第二个的行抵消掉。当M、N、k相同的时候，得到的结果肯定也是M*N。

如果两个矩阵想相乘，第一个矩阵的列必须要和第二个矩阵的行相同。两个k是相同的。而得到的结果却是一个M*N。

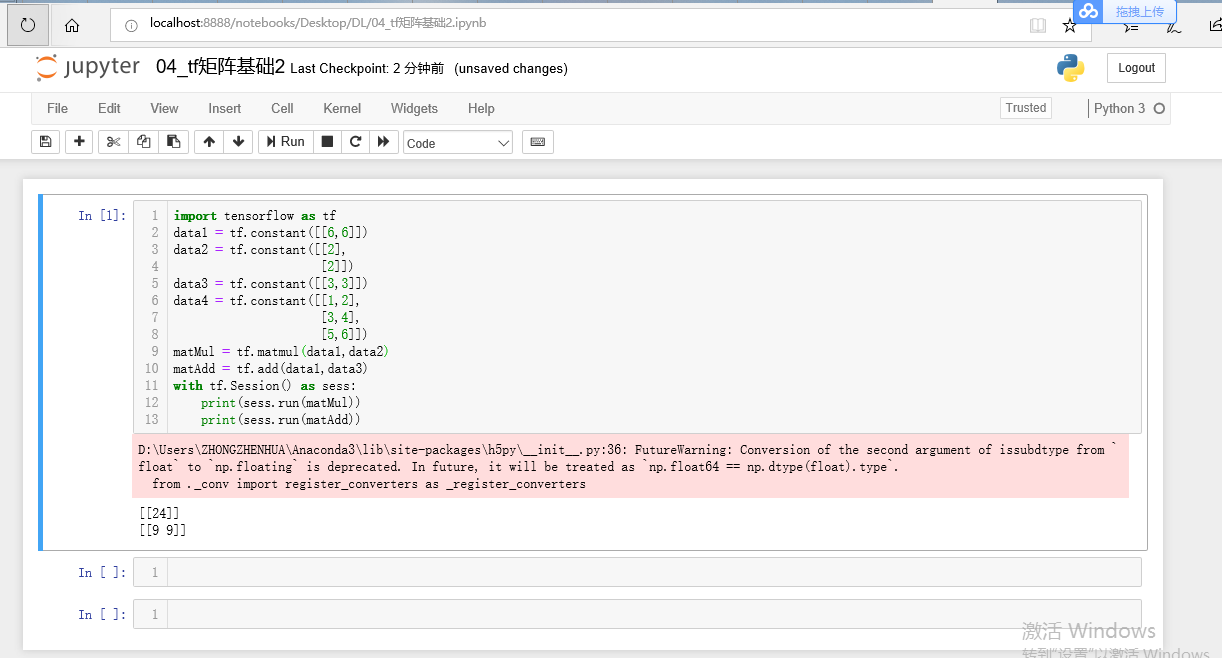
import tensorflow as tf
data1 = tf.constant([[6,6]])
data2 = tf.constant([[2],
                     [2]])
data3 = tf.constant([[3,3]])
data4 = tf.constant([[1,2],
                     [3,4],
                     [5,6]])
matMul = tf.matmul(data1,data2)
matAdd = tf.add(data1,data3)
with tf.Session() as sess:
    print(sess.run(matMul))
    print(sess.run(matAdd))

data1是1行两列，data2是两行1列。加法必须要是两个矩阵的维数相同，第一个矩阵data1是1行两列，第二个矩阵data3也是1行两列，那么它们执行的结果同样也是一个1行两列，所以输出是[[9 9]]。

---

第二种乘法是对应的元素相乘，和矩阵的加法比较类似。矩阵的加法必须要保证两个矩阵的维数M和N完全相同。而multiply则没有这个要求，所以这种乘法大家一定要注意。

import tensorflow as tf
data1 = tf.constant([[6,6]])
data2 = tf.constant([[2],
                     [2]])
data3 = tf.constant([[3,3]])
data4 = tf.constant([[1,2],
                     [3,4],
                     [5,6]])
matMul = tf.matmul(data1,data2)
matMul2 = tf.multiply(data1,data2)
matAdd = tf.add(data1,data3)
with tf.Session() as sess:
    print(sess.run(matMul))#1 维 M=1 N2. 1*2(MK) 2*1(KN) = 1*1
    print(sess.run(matAdd))#1行2列
    print(sess.run(matMul2))# 1*2 2*1 = 2*2 对应元素相乘 两个矩阵的最高维度都是2
    print(sess.run([matMul,matAdd]))