这一块的题解起来比较容易,产生一些容易让考生混淆的一些东西.
准并行,并不是完全意义上的并行处理.那么流水线它是如何提高速度的呢?是不是我一条指令要运行,只要采用了流水线这一个技术,就能够提高这一个指令的运行速度呢?答案是否定的.你用流水线来执行一条指令,和没用流水线它的速度是一样的.为什么是一样的呢?我们就要分析流水线是依仗什么来节省时间,如何提高设备的利用率,了解到了这一点我们以后的一些计算、一些概念的理解也就容易了.
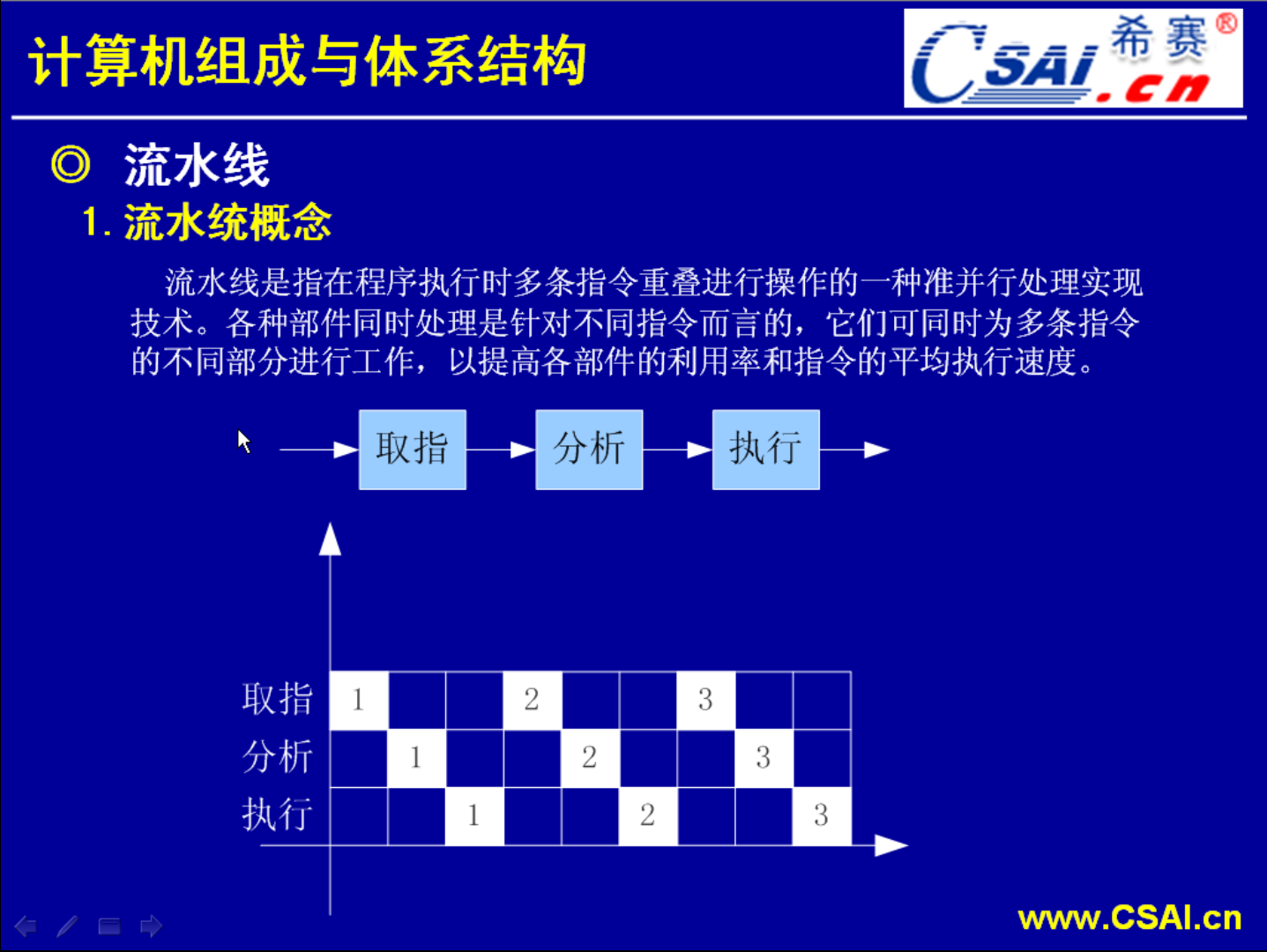
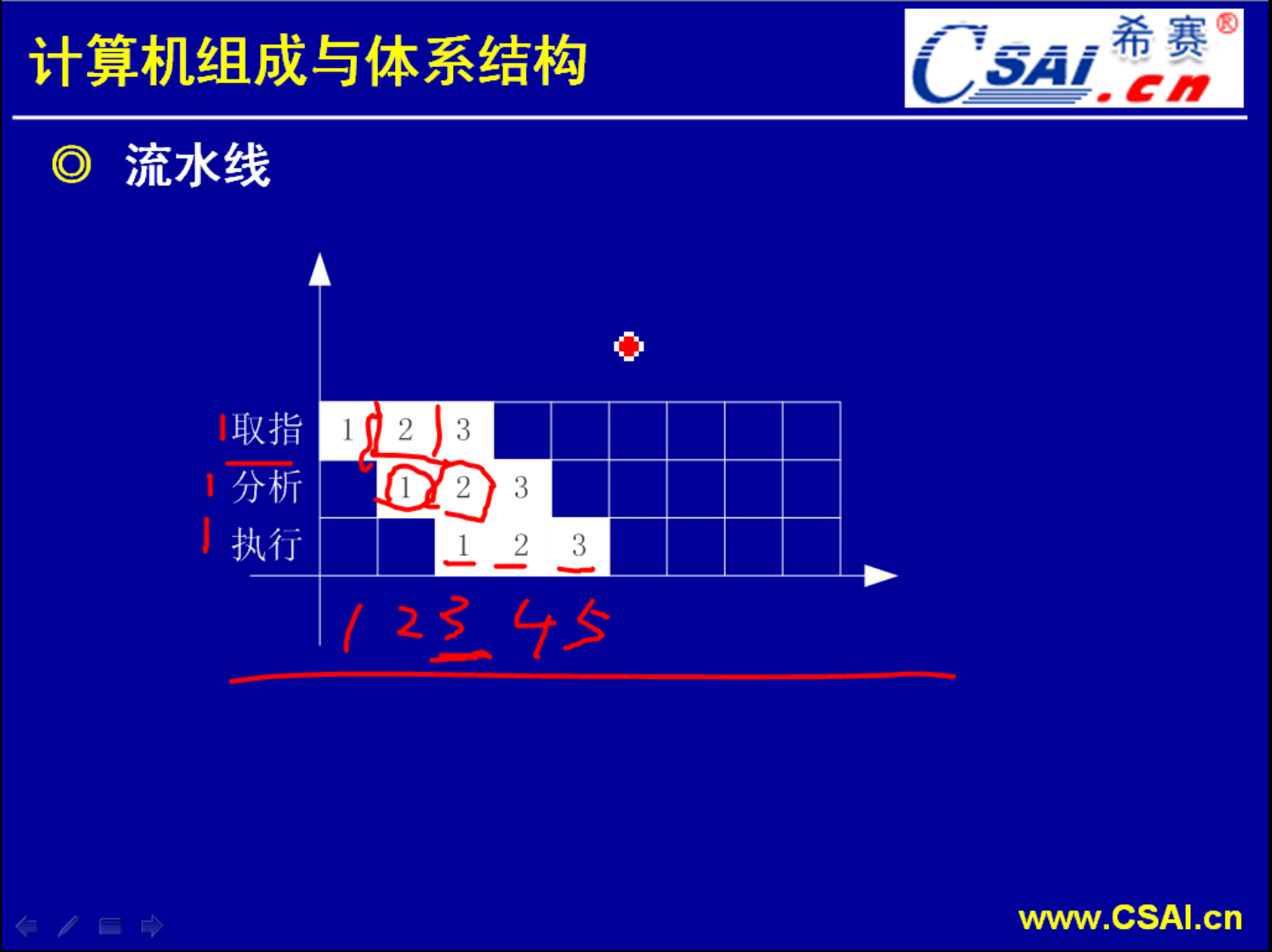
执行一条指令需要经过取址->分析->执行三个步骤,常规情况下我们指令一条一条的来处理,
为了好计算,取址、分析、执行都是定为1毫秒.那么三条指令执行下来就需要9毫秒,大家从这个图就可以看出一点设备的利用率非常的低.取址只有在1、4、7毫秒的位置才使用,其他的位置时刻2、3毫秒、5、6、毫秒、8、9毫秒这些时候设备都没有利用上来,在空闲.
因为在执行一条指令的时候它只有1/3的时间在取址,取址的这个设备做完取址的工作以后它就空闲了,空闲了就等到下一条指令的时候才会要用到.所以这样子中间就产生了很多设备的空闲,产生了设备的空闲那么我们就要想办法如何解决这个问题,那么流水线就是解决这种问题非常好的一种方式.它对这个执行过程进行了压缩和紧凑.
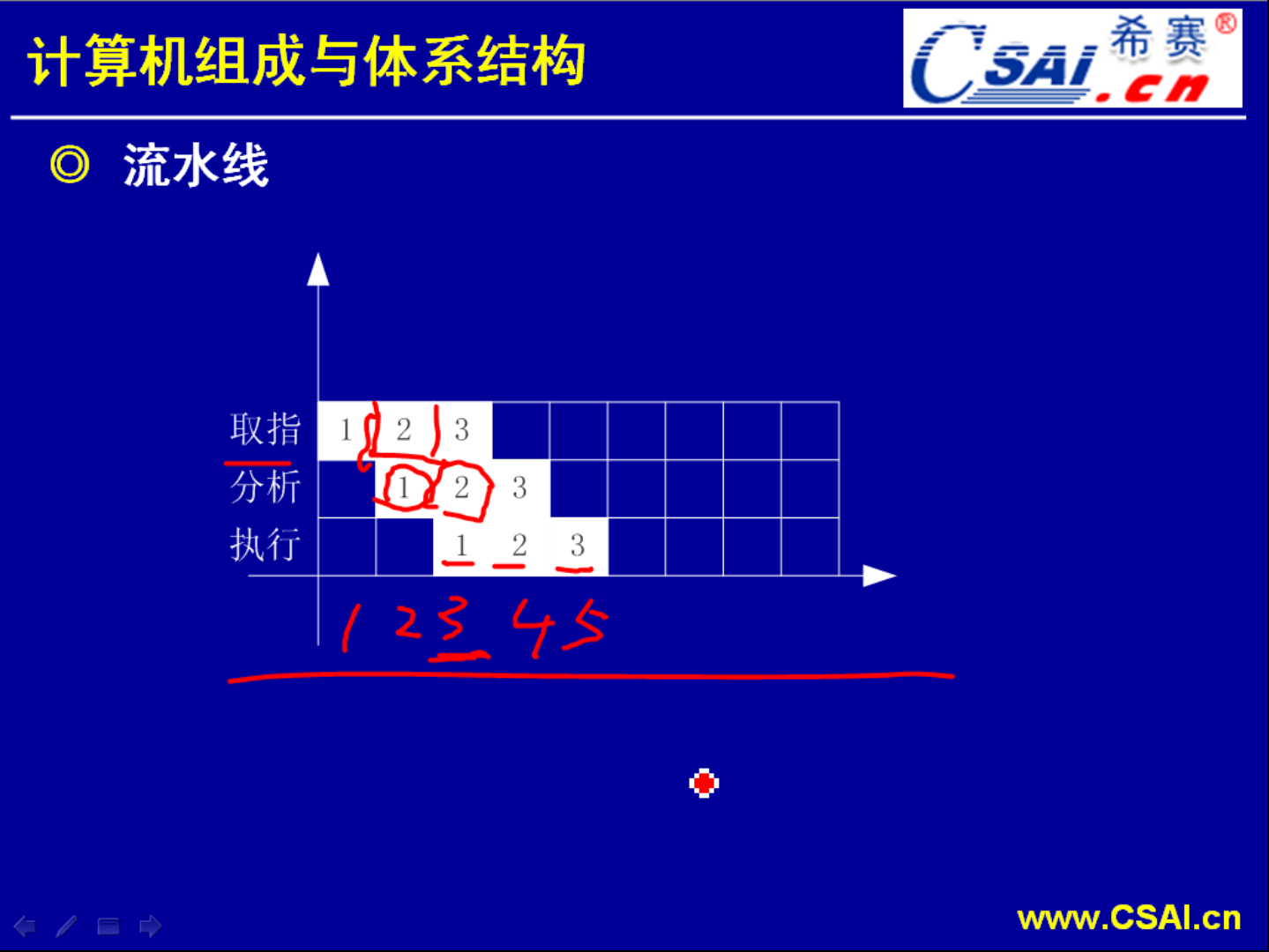
这就是一个流水线执行的一个时空图.它按这个设备进行了细分.取址的设备只要完成了第一条指令的取址它就立即进入第二条指令的取址.第二条指令取址完毕之后马上取第三条.
分析这一步也是一样.一条执行完之后立即执行第二条,再执行第三条.所以我们就从这两个图可以直观地看出实际上流水线执行这三条指令就已经占了很大的优势.因为它在五毫秒的位置就能够把三条指令全部执行完毕.但如果系统只有一条指令,那情况是如何的呢?如果只有一条指令,它要第三毫秒才能完成,和不利用流水线情况是一样的,都是三毫秒完成.所以利用流水线它并不能够提高单个指令它的运行速度,也不能够说把取址由以前的1毫秒压缩到0.5毫秒来完成.并不是这样子的,而是它把中间空闲的设备利用起来了,减少了空闲时间.所以它提高了速度而不是因为提高它的效率、不是提高执行速度、执行效率来提高速度.
理解了这一点,后面的问题也就好解决了.

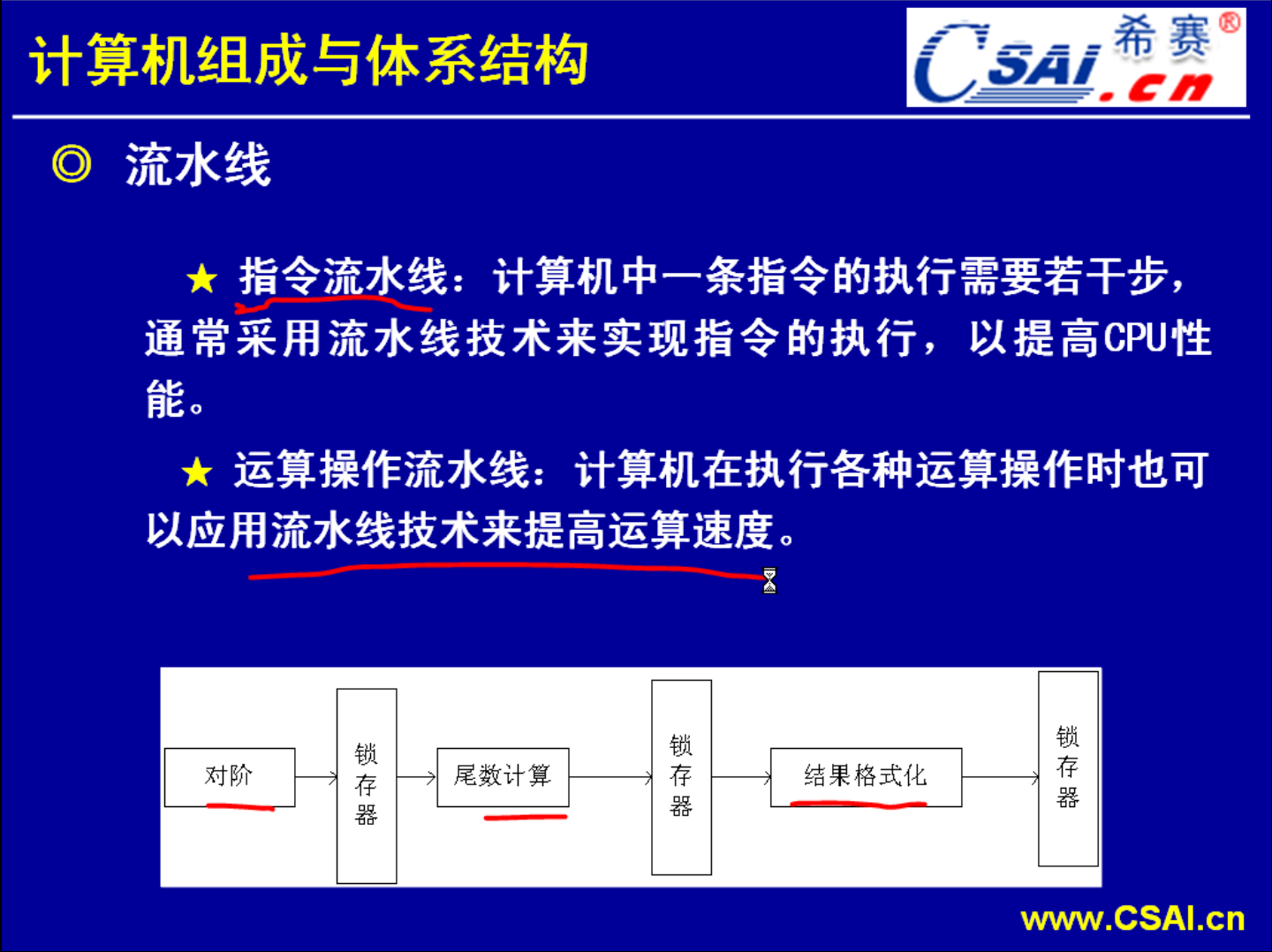
主要有哪一些类别的流水线.如果说某一个运算过程、做某一件事情要用到流水线,它必须这一件事情分几个阶段完成.用的最多的就是指令流水线,也就是我们刚才示意图的那种,就是指令它的执行要分成几个步骤,这几个步骤就成为了流水线的几个阶段,然后运算操作的时候也有可能应用到流水线的技术.因为运算的时候你比如说浮点运算,浮点运算它就要进行对阶->尾数计算->结果格式化等等操作.这些操作都是分阶段进行的,我们可以用流水线提高它的运算速度.
实质性的问题:如何求解流水线指令运行的时间.
比如说像这种情况,每一条指令的运行分三个步骤,它们分别是多少时间.然后我总共要执行多少条指令,执行这些指令用流水线技术完成需要多少时间,这是考题当中出现的最为频繁的一类题.
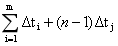
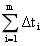 从i=1到i=m,这是一条指令运行所要花费的时间,
从i=1到i=m,这是一条指令运行所要花费的时间,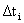 表示第几步要花费的时间.
表示第几步要花费的时间.
比如说 就表示指令执行的第一个阶段要花费多少时间,我们刚才所说的就是1毫秒.
就表示指令执行的第一个阶段要花费多少时间,我们刚才所说的就是1毫秒.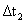 指令运行的第二步,也就是对应刚才的这个分析这一步要用多少时间.然后就是执行要用多少时间.
指令运行的第二步,也就是对应刚才的这个分析这一步要用多少时间.然后就是执行要用多少时间. 、
、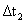 、
、 都是1,把它们加起来这样子就是公式的前一部分,就是1+1+1,后面这一部分有一个
都是1,把它们加起来这样子就是公式的前一部分,就是1+1+1,后面这一部分有一个 ,
,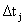 是指的流水线当中也可以说是指令执行过程中最慢的一个步骤.
是指的流水线当中也可以说是指令执行过程中最慢的一个步骤.
当然我们刚才举的例子比较极端,t1、t2、t3它都是相等的,都是1.那么1也就是最大值了.就是1+1+1+(n-1)*1.这样子就能够计算出总运行所要花费的时间.
具体的例题:
 就是指的这几个部分当中最耗时间的一部分.2、2、1,所以最耗时间的是2纳秒.
就是指的这几个部分当中最耗时间的一部分.2、2、1,所以最耗时间的是2纳秒.

再来一道软考当中出现过的题:
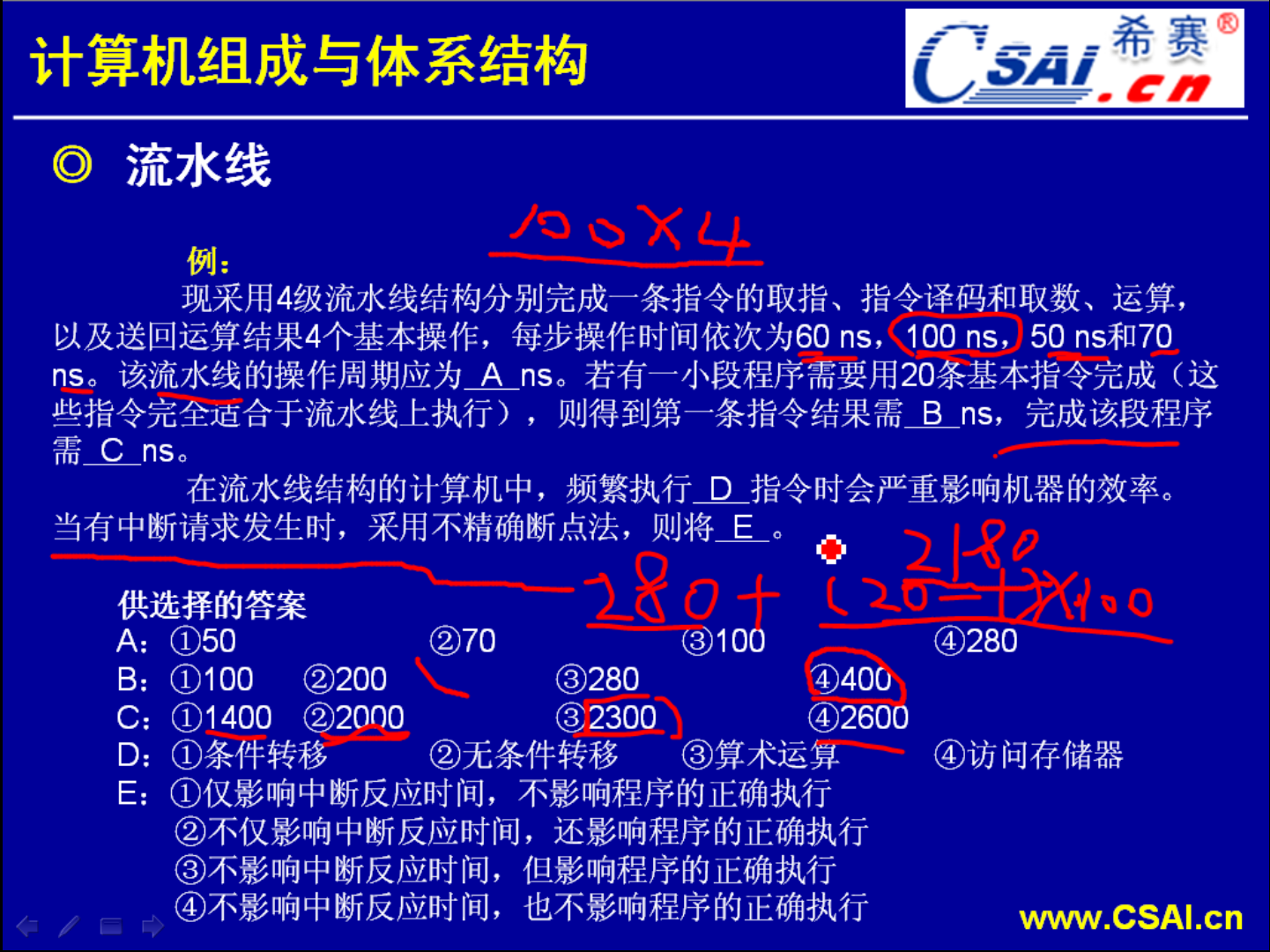
操作周期其实就是 ,也就是各个步骤当中运行的最慢的一段就作为流水线的操作周期.完成第一条指令其实很容易计算,就是60+100+50+70得到,结果加出来的数值应该是280.完成这段程序需要多少纳秒?用280+(20-1)*100=2180.很多人都求出这个数,但是问题是答案中没有这个数可选.所以有人质疑,流水线的计算到底它前面的一部分,前面的几条指令,第一条指令它的执行是每个周期都按最大的值执行,还是按这个每一步原有的这个值来执行.
,也就是各个步骤当中运行的最慢的一段就作为流水线的操作周期.完成第一条指令其实很容易计算,就是60+100+50+70得到,结果加出来的数值应该是280.完成这段程序需要多少纳秒?用280+(20-1)*100=2180.很多人都求出这个数,但是问题是答案中没有这个数可选.所以有人质疑,流水线的计算到底它前面的一部分,前面的几条指令,第一条指令它的执行是每个周期都按最大的值执行,还是按这个每一步原有的这个值来执行.
实际上正确的答案应该是这种形式.把流水线每一步包括第一条指令的执行都统一周期为100纳秒,这种做法是不合理的.为什么不合理呢?
再来看一个历年试题:

这种题出现比较多,而且我们平时画这个流水线的一个时空图的时候,也会给人一种错觉.我们平常画流水线的时空图是这样画的,

就包括第一条指令,它的每一个周期都是一个恒定的值.但是这种画法是不科学的.我们可以再细化来分析这一个流水线的一个执行图,
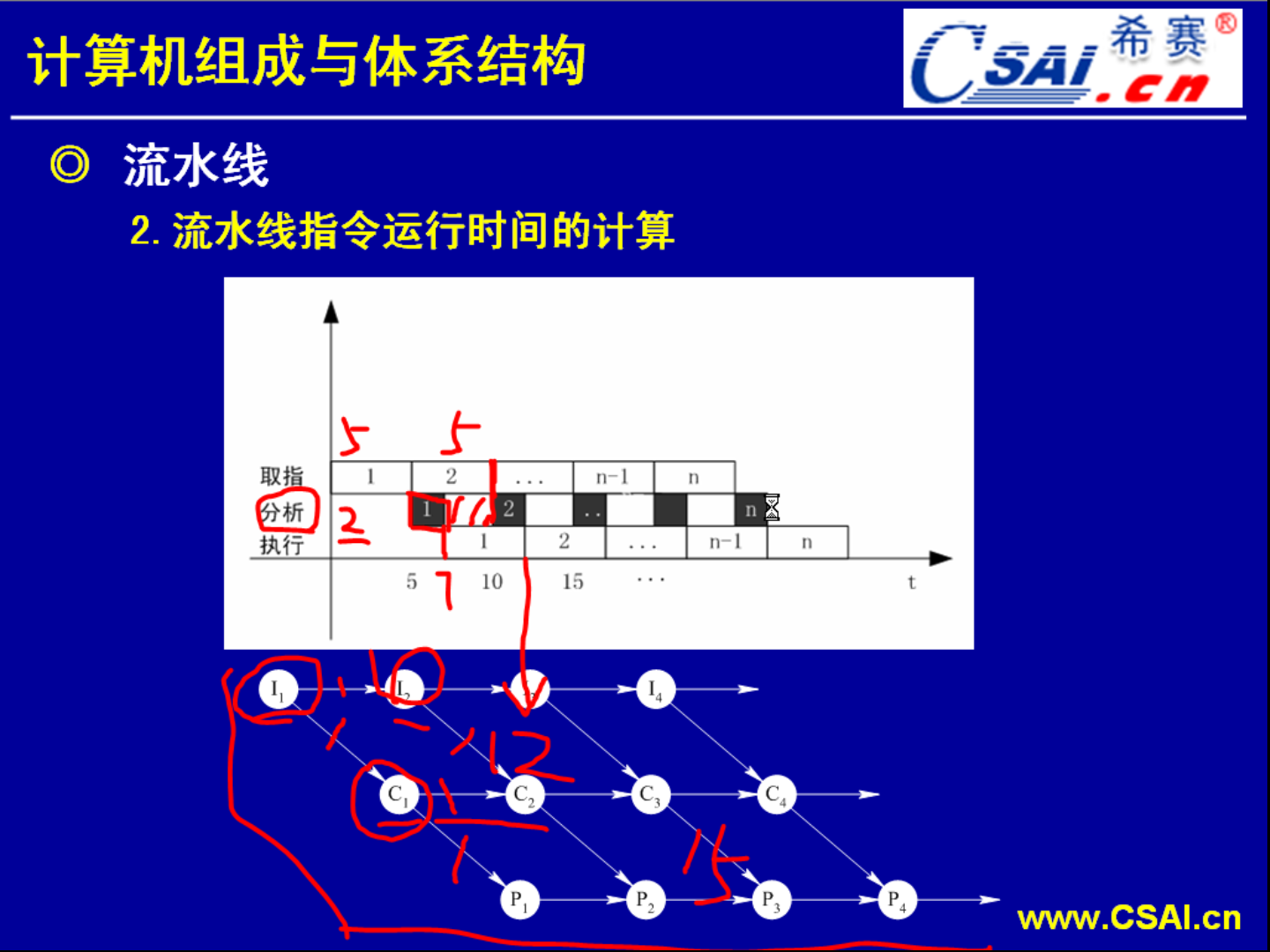
这一段是5纳秒,由于取址需要5纳秒,就是2号指令进行取址所用到的时间.但是分析只需要2纳秒,如果说这一段有5纳秒,那么这个执行过程就有技巧性可言了,就是说我这个2纳秒是在前一部分执行呢还是在后一部分执行.如果说这一个分析这一个步骤是在取址之后立马就执行的话它只需要2纳秒也就是总共时间运行到7纳秒的时候就完成了分析这一个动作,就可以进入第三部分的执行了.这样子一执行下来,我们就发现第一条指令实际上在12纳秒的时候就已经执行完了,而不必等到15纳秒.我为什么提出来这个分析时间可以在取址之后马上就执行呢?我们结合一个操作系统当中讲过的一个内容来看待,就是前趋图.这一个图就是流水线执行的一个前趋图,这个图中就把它们之间的一个逻辑一个关系执行的顺序的关系写的非常的清楚了.第一条指令的取址完成之后这两条线就去掉了,就是I1->I2和I1->C1执行的因素就去除了,就表明I2和C1可以开始运行了.而当C1运行完之后,C1->C2和C1->P1的条件也去除了.但是这里还有一个因素,C2不但是要C1完成,还要I2完成才能够执行C2.
所以从这个流水线的图我们也可以看出,虽然分析这一步分析完了I1,分析完了第一条指令,但是这一部分还是处于一个空闲的状态,没有分析I2.而等到I2的取址取完了之后,才执行C2的.所以用这一个前趋图分析这一个过程就可以比我们光看这一个流水线的示意图要清楚一些.它们之间的关系会明了一些.所以说正规的计算方式应该就是我们开始公式所指出来的,就是用1条指令它的执行时间加上(n-1)*周期时间 .如果说我们考试遇到了这种类型的题,应该要如何处理呢?然后如果遇到这种问题,我们清楚2180才是正确的.这一点没错但是为了得分,因为我们这里面没有2180,我们得考虑第二种方案:就是每一个周期都相等的,每一个周期都相等的我们再来计算一次.就是第一条指令变成了4个周期都是100,所以100*4+(20-1)*100=2300.而第一条指令的执行时间为400纳秒.
.如果说我们考试遇到了这种类型的题,应该要如何处理呢?然后如果遇到这种问题,我们清楚2180才是正确的.这一点没错但是为了得分,因为我们这里面没有2180,我们得考虑第二种方案:就是每一个周期都相等的,每一个周期都相等的我们再来计算一次.就是第一条指令变成了4个周期都是100,所以100*4+(20-1)*100=2300.而第一条指令的执行时间为400纳秒.
这样子来灵活处理,首先按常规方式计算,计算得不到答案我们就用等周期的进行计算,答案之中不可能会两种都出现.

下面我们来看流水线相关的第二个计算:流水线的吞吐率.
流水线的所有的计算其实都是基于我们刚才讲的流水线运行时间的一个概念来进行扩充的,这个吞吐率就是这样子的.
Tk也就是我们刚才所计算出来的运行n条指令所要花费的时间.n是所运行的指令的条数.

流水线的吞吐率是怎么来计算的?比如这一个题我们计算出总时间为203纳秒,而指令条数为100,用100除以203得到的就是吞吐率TP.这个计算很容易.

再看一个吞吐率的考试的考题.
不清楚的是执行这10条指令所要花费的时间. 我们就可以先计算出总时间来,总时间套公式就可以了.1条指令所要花费的时间再加上(n-1)*周期,这里面周期是3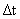 ,3
,3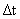 是执行时间最长的.
是执行时间最长的.

下面我们再来看流水线的加速比.

这些概念是相当重要的.如果说告诉你这个加速比的概念,在考场上要你求加速比,肯定很容易就求出来了.因为不使用流水线和使用流水线所用的时间都很容易求.但是一旦你如果说这个加速比的概念都不清楚,那么解题就困难了.所以大家在平常应该多注意一些这种概念、这种公式,把这些东西记下来,然后再记一些基本的运算.这方面的题也就不成问题了.
不用流水线所用的时间是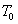 ,使用流水线所用的时间为
,使用流水线所用的时间为 ,用
,用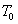 比
比 就得到了加速比.我们可以以这一个试题为例,这里我们已经求出了利用流水线它所要消耗的时间,不利用流水线执行10条指令所要花费的时间更好计算,就用(
就得到了加速比.我们可以以这一个试题为例,这里我们已经求出了利用流水线它所要消耗的时间,不利用流水线执行10条指令所要花费的时间更好计算,就用(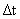 +3
+3 +
+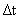 +2
+2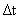 +
+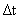 )*10就可以了.它们相加之后是8
)*10就可以了.它们相加之后是8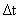 ,也就是说执行单条的指令需要8
,也就是说执行单条的指令需要8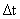 的时间,所以执行10条的指令不用流水线就要80
的时间,所以执行10条的指令不用流水线就要80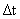 .我们用80
.我们用80 除以35
除以35 就得到了加速比.也就是顺序执行的时间除以35
就得到了加速比.也就是顺序执行的时间除以35 也就是流水线执行时间.这样子我们就得到了加速比.加速比的公式就是这个公式.
也就是流水线执行时间.这样子我们就得到了加速比.加速比的公式就是这个公式.

再看一个例题.
唯一的一点不同就是没有告诉你指令的条数.但是这个不要紧,我们可以用n代表指定的条数.把这五段时间加起来乘以n得到的就是不使用流水线所要花费的时间,而用底下这种方式就是一条指令执行所消耗的时间加上(n-1)乘以流水线周期得到的就是使用流水线所要花费的时间,然后一比就得到了结果.就是4n/4+n-1.然后最大加速比我们可以用一个极限的公式把它求出来,就是当这个指令的数量趋向于无穷大的时候这个n:指令的数量趋向于无穷大的时候,这个加速比为4,也就是说它可能产生的最大加速比就是4.

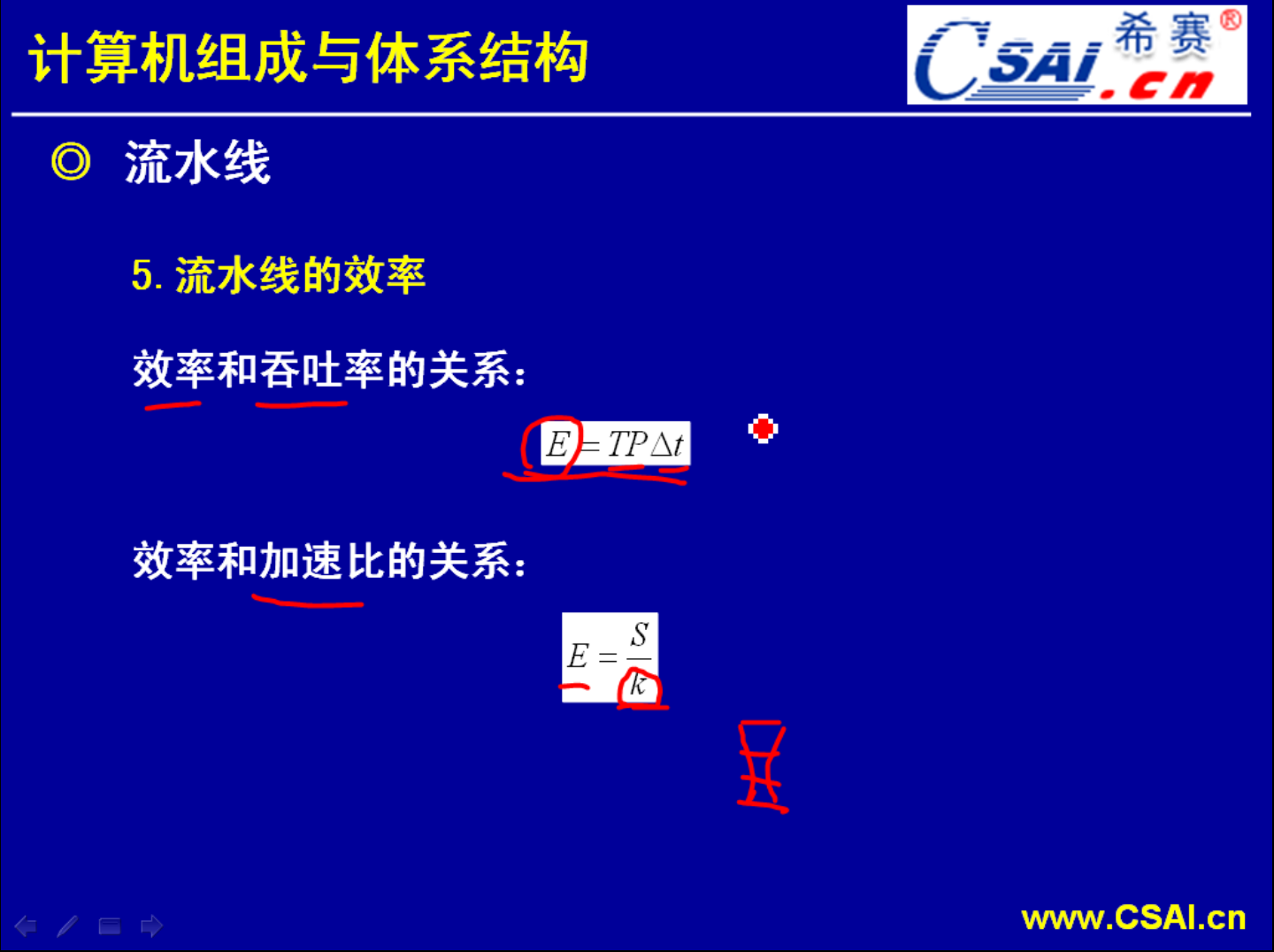
最后一点来讲一讲流水线的效率.
这个效率可以和吞吐率牵上关联.效率E=吞吐率TP*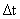 .或者说用加速比来求这个效率,加速比S除以k也能够得到效率.k就是流水线所分的级数.比如我们开始讲的把一条指令分为取址、分析、执行三个步骤,那么k=3.像刚才的五段流水线,那么k=5.像这种分为五级那么k=5.其实效率也很好计算,可以根据前面的执行结果计算出来.
.或者说用加速比来求这个效率,加速比S除以k也能够得到效率.k就是流水线所分的级数.比如我们开始讲的把一条指令分为取址、分析、执行三个步骤,那么k=3.像刚才的五段流水线,那么k=5.像这种分为五级那么k=5.其实效率也很好计算,可以根据前面的执行结果计算出来.