本节课我们来学习一种新的查找方式叫做散列查找。什么是散列查找呢?在学习散列查找之前,一定要介绍一个基本概念就是散列表。那么学习散列表之前我们先来回忆一下之前所学习过的所有查找方式,那么无论是顺序查找还是折半查找,还是之后学习的新的数据结构——B树、B+树,它们的查找方式都是基本比较的基础上的。我们都要通过比较来找到我们想要找到的元素的位置。那么本节课所学习的散列表、散列查找是一种全新的查找的概念,我们不用通过比较的方式就可以直接找到对应元素的位置。

那么我们先来看一个实际生活中的小例子。那么这是一群小朋友,我们让他站成了一排,根据我们之前的查找方式,那么它大体都是我们依次地比较,找到对应我们想要找的那个小朋友的位置,看一看哪一个位置是我们所要找的那一个小朋友。那么对应如果是散列查找呢,我们观察这些小朋友是不是按照彩虹的顺序,赤橙黄绿青蓝紫的顺序进行排列的。那么如果我们知道彩虹顺序,我们就一定知道小红一定是排在一号位置的,小黄应该是排在二号位置的,小橙应该是排在三号位置的,等等等等。那么这样我们是不是就不用通过一次比较来找到每个小朋友的位置了。我们通过一个基本常识直接让小红映射到了一号位置,小黄映射到了二号位置,依此类推。那么这样的方式,这样的概念,其实就有点类似我们今天所要学习的散列查找、散列表。那么散列查找就是通过了一种映射手段让我们每一个数据元素映射到存储空间上的一个特定的位置。
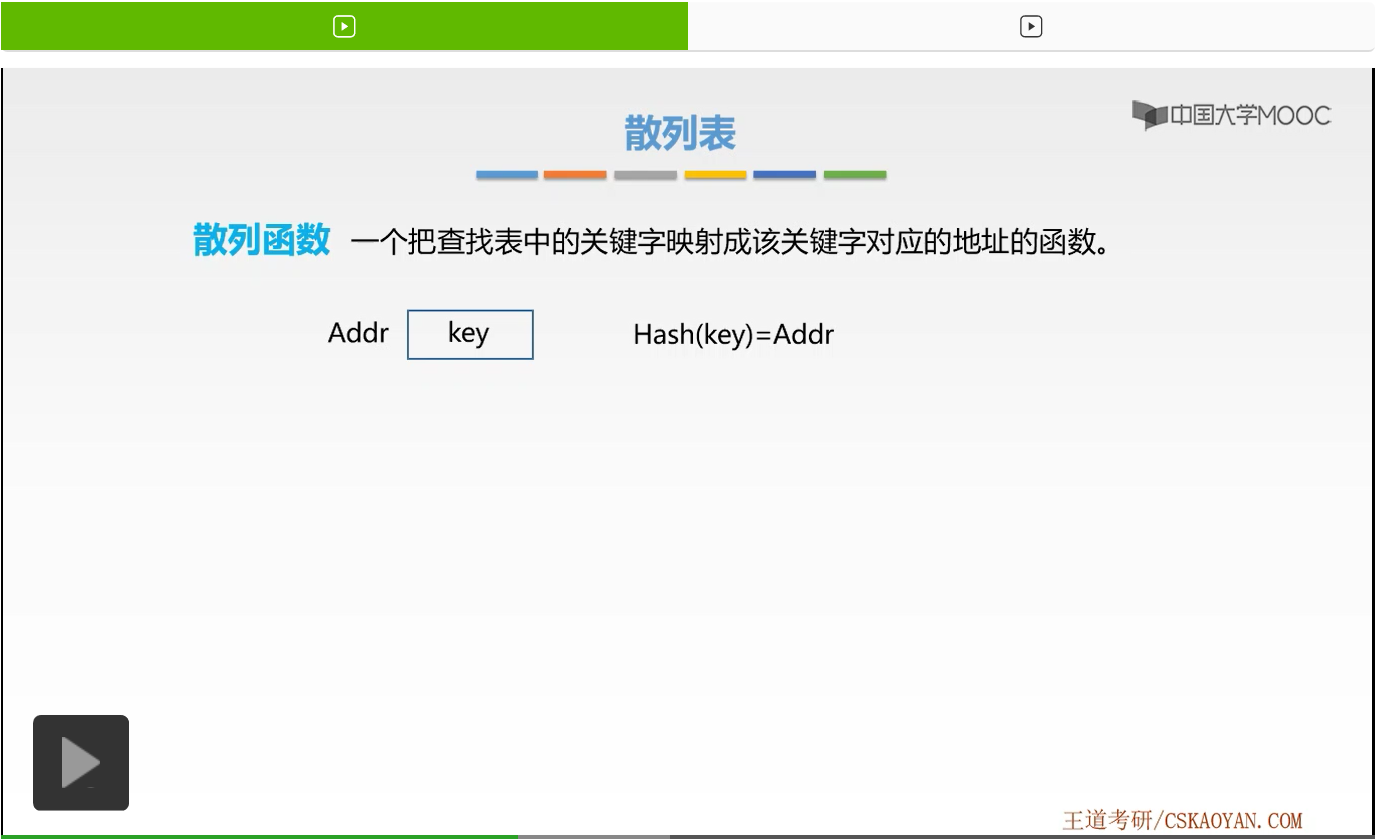
那么在散列表当中,我们是通过什么样的形式来表示这样的关系呢?我们是通过散列函数来表示的。那么这样一个把查找表中的关键字映射成该关键字对应的地址的这样一个函数就叫做散列函数。我们来看,如果现在有一个存储单元,它的地址为Addr。如果它存放的关键字为key的话,那么我们就用这样的散列函数表示了key与Addr的关系,也就是我们通过对key传入到函数Hash中进行计算,就可以算得Addr这样一个值。Addr恰好是key对应存储单元的地址。那么这就是散列函数的一个作用和表示。
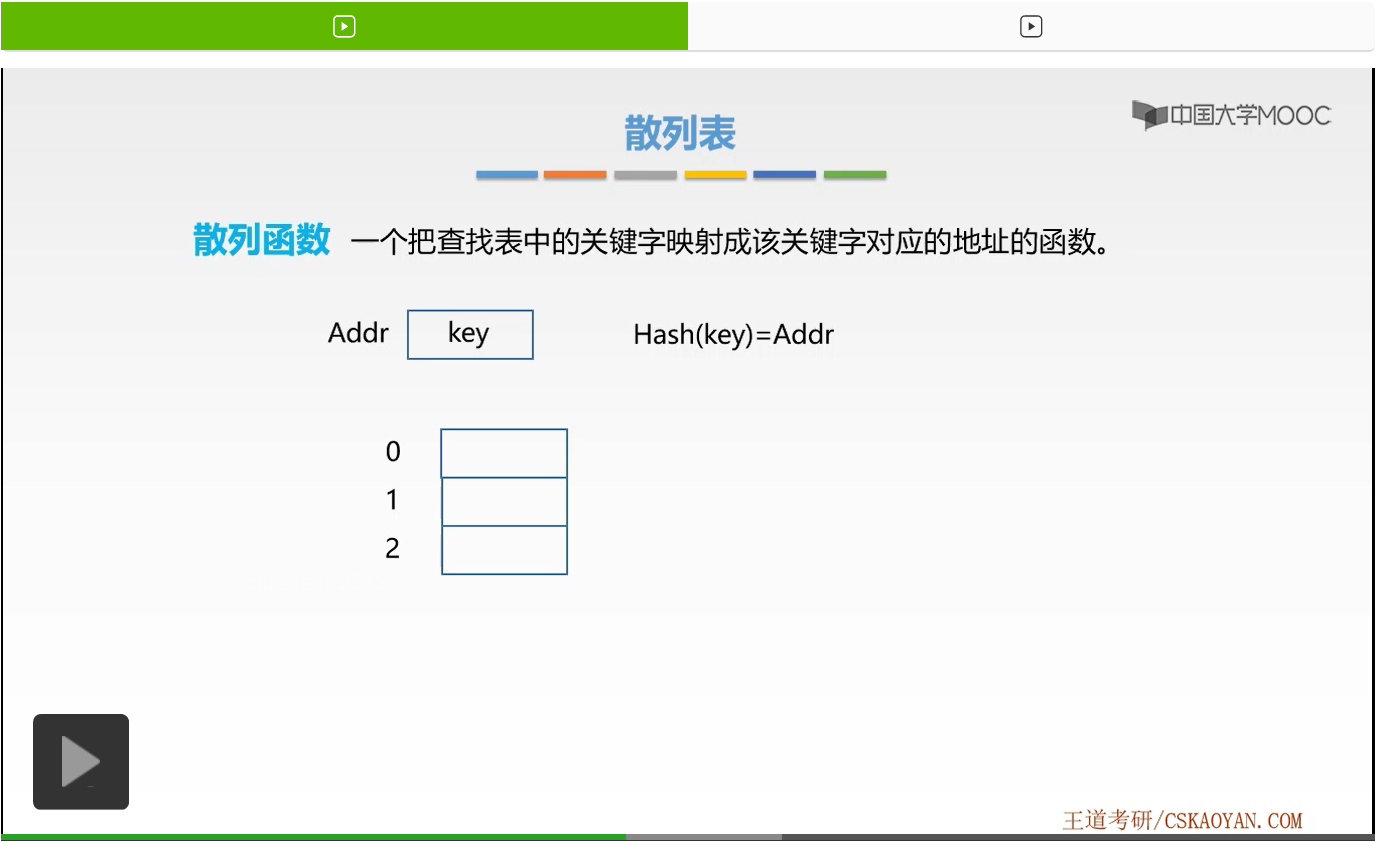
接下来我们来看一个小例子,现在我们有三个存储单元。大家发现了,它对应的下标是不是0、1、2啊。这里我们并没有用地址,所以大家千万不要有局限性,就是散列函数计算出的最终结果,可以表示为存储单元的地址,也可以表示为数组的下标或者是记录的索引。它只要可以表示我们对应想要查找的这一个关键字,这一个数据元素的位置就可以了。那么这里我们把它表示为数组的下标,那么现在我们有三个数组的位置。
假设现在我们规定散列函数Hash为一个取余函数,它如何计算呢?就是通过关键字取余3来计算出对应数组的一个下标。
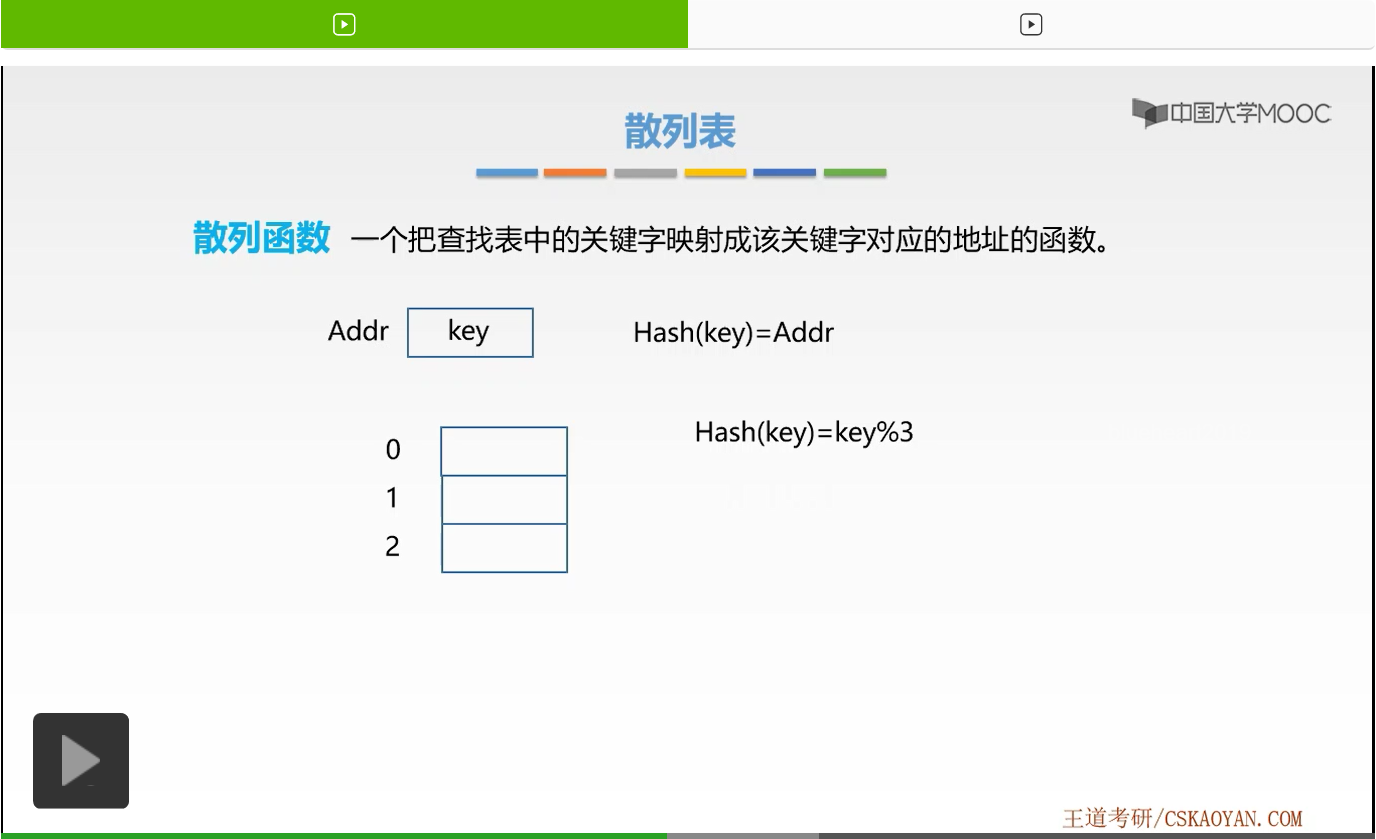
假设现在我们要存放的三个整数为,{6,13,26}。它是如何通过散列函数进行存放的呢?例如我们来看第一个数字6,6通过key取余,6现在是key,6取余3,它是不是得到0啊。那么6就存放在数组下标0的位置。那么13,取余3之后,得到的是1,所以它存放在数组下标1的位置。那么26取余之后得到的结果是2,所以它存放在数组下标2的位置。这样我们是不是就存放了6、13、26这样三个数字啊。我们是通过对应的规定的散列函数来将它们进行存放的。那么我们发现,如果我们想要找到关键字13的位置,是不是就可以通过13取余3,那么13存放的就是数组下标为1的这样一个位置啊。我们可以通过散列函数Hash这样一个散列函数直接计算出每一个数字对应存放的数组下标。这就是散列函数的使用过程以及我们拿到散列表这样一个目的。
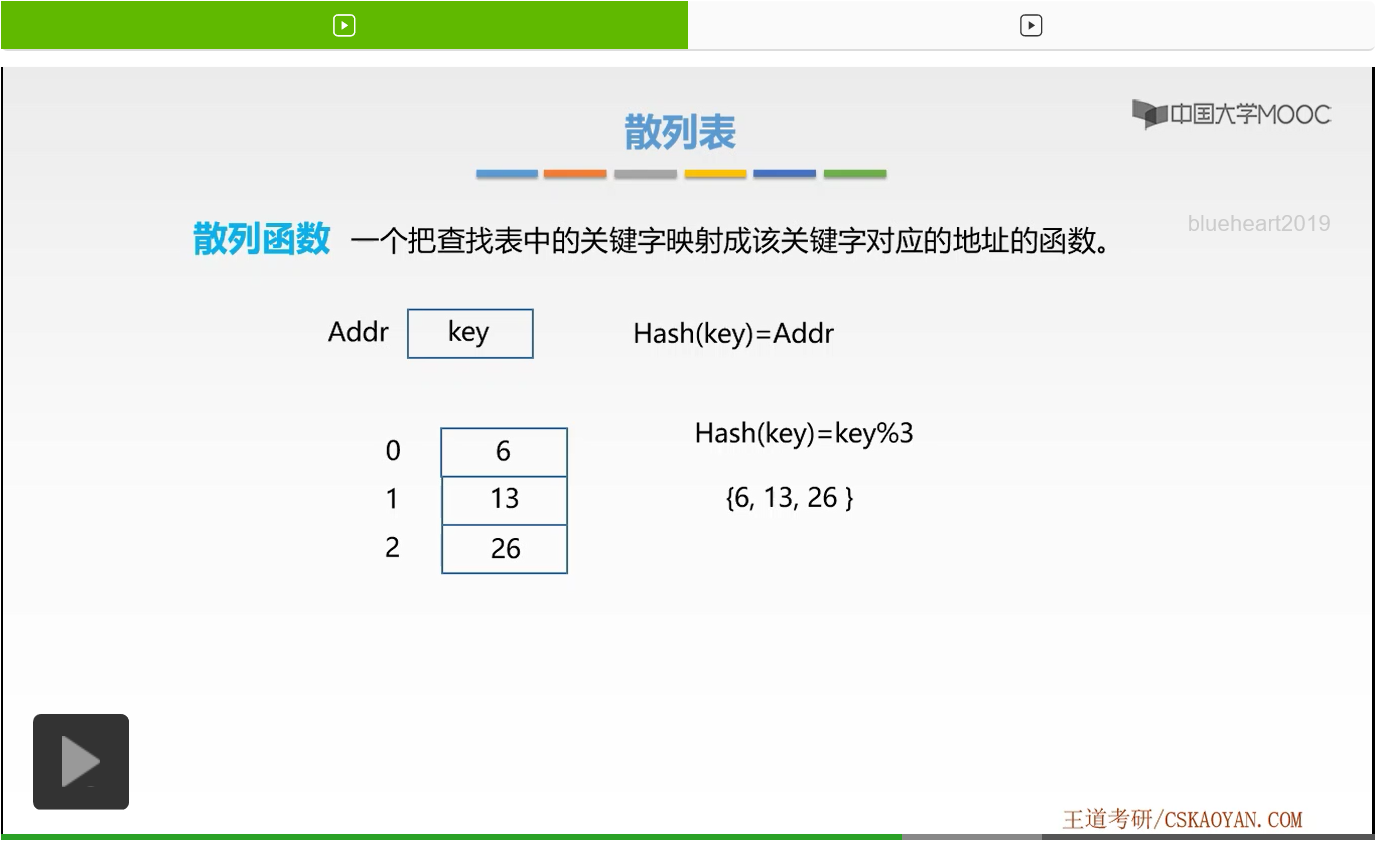
那么接下来大家是不是就知道什么是散列表了?我们根据关键字而直接进行访问的数据结构,就如我们上一个举的这样一个例子的数据结构,它建立了关键字与存储地址之间的一种直接映射关系。我们称这样的一种结构就叫做散列表。那么我们观察,上一个例子是不是就是一个散列表的例子啊。我们将每一个关键字都与它对应的直接访问的地址建立了一种直接的映射关系。散列表的查找是不是直接可以通过散列函数直接找到对应关键字的存储单元,对应关键字的下标啊。那么这样的时间复杂度是不是就是大O1(O(1))啊。那么它既然比我们之前所学习的比较、基于比较的查找方式来的要更快,而且效率要更高的话,为什么没有得到广泛的应用呢?其实它存在一个问题,就是冲突的问题。什么是冲突的问题呢?我们来观察,现在我们把数字6存放在数组下标为0的位置,因为我们通过取余的这样一个散函数计算得到的它的对应下标。那么例如我们现在又要存放一个数字,存放3的话,我们通过3取余3,是不是也要存放在数组下标0的位置啊。这样我们就产生了冲突,因为我们把两个不同的数字、两个不同的关键字映射到了同一个存储单元下,它们的地址是相同的。
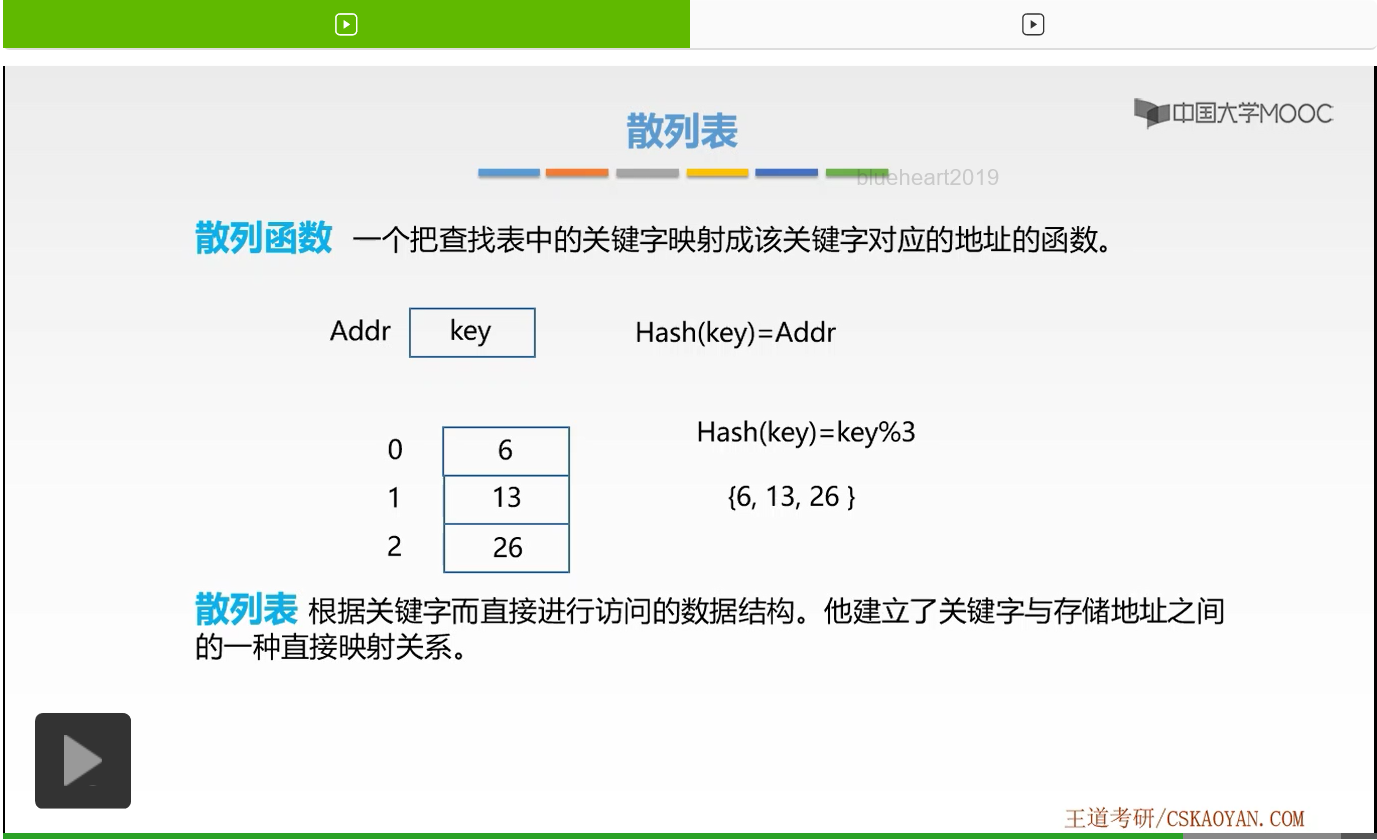
所以我们就有这样冲突的概念。散列函数可能会把多个不同的关键字映射到同一地址下的这样一种情况,就叫做冲突。所以为什么散列函数、散列表没有得到广泛的应用呢?因为它存在这样这样一个冲突的问题。虽然我们查找的效率可能在理想的情况下会非常高,但是如果产生冲突的话,它的查找效率也会降低下来。那么其实这样的冲突是无法避免的,所以在我们接下来的学习过程当中,主要学习的一点就是如何设计好散列函数来尽量减少冲突的发生。并且,如果冲突发生了,可以不让这些冲突影响我们对应的查找,这就是我们下一节课所要学习的主要内容。

上一节课我们学习了有关散列表的基础知识,了解了什么是散列表以及它是如何进行查找的。那么本节课我们就来学习散列表的其他重要的基本知识,就是散列函数的构造方法,冲突处理的方法以及散列表的性能分析。
首先我们先来学习一下散列函数的构造方法。如何构造一个散列函数呢?我们先来回忆一下散列函数的基本概念。它是一个把查找表中的关键字映射成该关键字对应的地址的这样一个函数。下面是我们的计测方法。Hash(key)我们最终求得的值是我们对应存储单元的地址Addr,那么散列函数我们无论是在构造散列表的过程当中还是在散列表中进行查找时,都要用到这样的函数。
那么如何构造它呢?我们先来看一下它的构造要求。第一个要求是散列函数的定义域必须包含全部需要存储的关键字,这一点是必然的,为什么呀。如果定义域不包含我们所要存储的关键字的话,那么这些关键字就无法通过散列函数映射到对应的存储单元上了。而下一句是,值域的范围则依赖于散列表的大小或地址范围。这一点也是非常好理解的。因为如果我们对应求得的这样一个值,无法求算出我们散列表中的每一个存储单元的地址的话,那么这些地址的存储单元是不是就浪费了?所以值域的范围则依赖于散列表的大小或者地址的这样一个范围。
那么第二个要求是什么呢?散列函数计算出来的地址,应该能等概率、均匀地分布在整个地址空间上,从而减少冲突的发生。因为,如果它不均匀地分布在地址空间上的话,如果我们所有求得的关键字,对应的映射到的地址,都是同一个的话,那么它们是不是都产生冲突了。所以我们要求它最好能够等概率、均匀地分布在地址空间上,这样可以减少对应冲突的发生。
而最后一点则是,散列函数应尽量简单,能够在较短时间内计算出任意关键字对应的这样一个散列地址。那么这一点大家也非常好理解。如果它非常难计算的话,我们对应的效率就会非常的低。好,讲解完了三个构造要求之后,接下来我们就来学习一下在散列函数当中会主要涉及哪些构造方法。