luogu4705玩游戏

题解

我们要对于每个t，求一个(1/mn)sigma(ax+by)^t。

把系数不用管，把其他部分二项式展开一下：

simga(ax^r*by^(t-r)*C(t,r))。

把组合数拆开，就变成了一个卷积的形式。

t!*sigma((ax^r/r!)*(by^(t-r)/(t-r!))

不用管前面的系数，那么我们的卷积数组就是

sigma(ax^i)/i!

所以这道题本质让我们快速求f(i)=sigma(ax^i)。

考虑生成函数

我们的f就是所有的这些生成函数的和。

然后上面的式子求和后变成

我们要求的就是所有这些东西的和。

考虑到

我么设G(x)为生面的式子，那么F(x)=-x*G(x)+n。

所以我们只需要求出G(x)就好了。

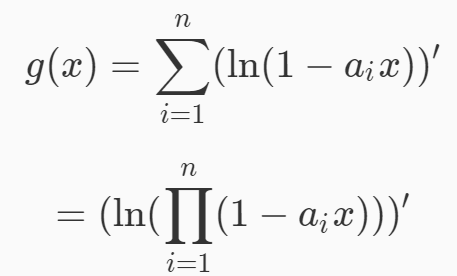
下面的那个连乘可以用分治乘法算出来，然后求个ln就好了。

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#define N 550002
using namespace std;
typedef long long ll;
const ll mod=998244353;
const ll G=3;
const ll Gi=332748118;
ll a[N],c[N],b[N],d[N],mem[45][N],cnt,jie[N],ni[N],bu[N],t,bb[N],mp[N]; 
int rev[N],n,m;
inline int rd(){
    int x=0;char c=getchar();bool f=0;
    while(!isdigit(c)){if(c=='-')f=1;c=getchar();}
    while(isdigit(c)){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
    return f?-x:x;
}
inline ll power(ll x,ll y){
    ll ans=1;
    while(y){if(y&1)ans=ans*x%mod;x=x*x%mod;y>>=1;}
    return ans;
}
inline void NTT(ll *a,int l,int tag){
    for(int i=1;i<l;++i)if(i>rev[i])swap(a[i],a[rev[i]]);
    for(int i=1;i<l;i<<=1){
        ll wn=power(tag==1?G:Gi,(mod-1)/(i<<1));
        for(int j=0;j<l;j+=(i<<1)){
            ll w=1;
            for(int k=0;k<i;++k,w=w*wn%mod){
                ll x=a[j+k],y=a[i+j+k]*w%mod;
                a[j+k]=(x+y)%mod;a[i+j+k]=(x-y+mod)%mod; 
            }
        }
    }
}
void solve(ll *a,int l,int r,ll *ans){
    if(l==r){ans[0]=1;ans[1]=mod-a[l];return;}
    int mid=(l+r)>>1;ll *a1=mem[++cnt];ll *a2=mem[++cnt];
    solve(a,l,mid,a1);solve(a,mid+1,r,a2);
    int len=1,L=0;
    while(len<=2*(r-l+1))len<<=1,L++;
    for(int i=1;i<len;++i)rev[i]=(rev[i>>1]>>1)|((i&1)<<(L-1));
    NTT(a1,len,1);NTT(a2,len,1);
    for(int i=0;i<len;++i)ans[i]=a1[i]*a2[i]%mod;
    NTT(ans,len,-1);ll ny=power(len,mod-2);
    for(int i=0;i<len;++i)ans[i]=ans[i]*ny%mod,a1[i]=0,a2[i]=0;
    cnt-=2;
}
void get_inv(ll *a,ll *b,int len){
    if(len==1){b[0]=power(a[0],mod-2);return;}
    get_inv(a,b,(len+1)>>1);
    int l=1,L=0;
    while(l<=(len<<1))l<<=1,L++;
    for(int i=1;i<l;++i)rev[i]=(rev[i>>1]>>1)|((i&1)<<(L-1));
    for(int i=0;i<len;++i)bu[i]=a[i];for(int i=len;i<l;++i)bu[i]=0;
    NTT(bu,l,1);NTT(b,l,1);
    for(int i=0;i<l;++i)b[i]=b[i]*(2ll-bu[i]*b[i]%mod+mod)%mod;
    NTT(b,l,-1);ll ny=power(l,mod-2);
    for(int i=0;i<len;++i)b[i]=b[i]*ny%mod;for(int i=len;i<l;++i)b[i]=0;
}
inline void get_dao(ll *a,int len){
    for(int i=1;i<len;++i)a[i-1]=a[i]*i%mod;a[len-1]=0;
}
inline void flag(ll *a,int len,ll *ans){
    int l=1,L=0;while(l<(max(len,(int)t)*2))l<<=1,L++;
    solve(a,1,len,ans);
    get_inv(ans,b,t);get_dao(ans,l);//!!!!!!!!!!!!!
    for(int i=1;i<l;++i)rev[i]=(rev[i>>1]>>1)|((i&1)<<(L-1));
    NTT(ans,l,1);NTT(b,l,1);
    for(int i=0;i<l;++i)ans[i]=ans[i]*b[i]%mod;
    NTT(ans,l,-1);ll ny=power(l,mod-2);
    for(int i=0;i<l;++i)ans[i]=ans[i]*ny%mod;
    for(int i=l-1;i>=1;--i)ans[i]=ans[i-1]*(mod-1)%mod;
    ans[0]=len;
    for(int i=1;i<=t;++i)ans[i]=ans[i]*ni[i]%mod;
    for(int i=t+1;i<l;++i)ans[i]=0;
}
int main(){
    n=rd();m=rd();
    for(int i=1;i<=n;++i)a[i]=rd();
    for(int i=1;i<=m;++i)bb[i]=rd();
    t=rd();
    jie[0]=1;for(int i=1;i<=t;++i)jie[i]=jie[i-1]*i%mod;ni[t]=power(jie[t],mod-2);
    for(int i=t-1;i>=0;--i)ni[i]=ni[i+1]*(i+1)%mod;
    flag(a,n,c);memset(b,0,sizeof(b));flag(bb,m,d);
    int l=1,L=0;
    while(l<=t*2)l<<=1,L++;
    for(int i=1;i<l;++i)rev[i]=(rev[i>>1]>>1)|((i&1)<<(L-1));
    NTT(c,l,1);NTT(d,l,1);
    for(int i=0;i<l;++i)c[i]=c[i]*d[i]%mod;
    NTT(c,l,-1);ll ny=power(l,mod-2);
    for(int i=0;i<l;++i)c[i]=c[i]*ny%mod;
    ny=power(1ll*n*m%mod,mod-2);
    for(int i=1;i<=t;++i)printf("%lld
",c[i]*jie[i]%mod*ny%mod); 
    return 0;
}