In our daily life we often use 233 to express our feelings. Actually, we may say 2333, 23333, or 233333 ... in the same meaning. And here is the question: Suppose we have a matrix called 233 matrix. In the first line, it would be 233, 2333, 23333... (it means a 0,1 = 233,a 0,2 = 2333,a 0,3 = 23333...) Besides, in 233 matrix, we got ai,j = a i-1,j +a i,j-1( i,j ≠ 0). Now you have known a 1,0,a 2,0,...,a n,0, could you tell me a n,m in the 233 matrix?
InputThere are multiple test cases. Please process till EOF.
For each case, the first line contains two postive integers n,m(n ≤ 10,m ≤ 10 9). The second line contains n integers, a 1,0,a 2,0,...,a n,0(0 ≤ a i,0 < 2 31).OutputFor each case, output a n,m mod 10000007.Sample Input
1 1 1 2 2 0 0 3 7 23 47 16
Sample Output
234 2799 72937
题意:
a[i][j]=a[i-1][j]+a[i][j-1];
a[0][1]=233,a[0][2]=2333,a[0][3]=23333,......
a[1][0]到a[n][0]由输入给出,求a[n][m];
思路:
本来打算直接用a[i][j]=a[i-1][j]+a[i][j-1]作为公式进行推导,发现并不可行。
实际上是直接对每一列进行操作。
写完这题,大概矩阵快速幂才是真的入门。
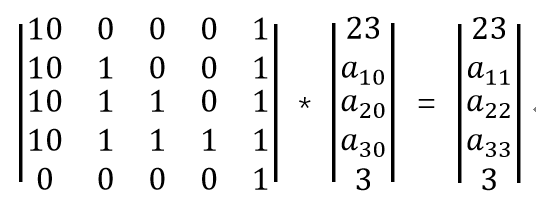

#include<iostream> #include<algorithm> #include<vector> #include<stack> #include<queue> #include<map> #include<set> #include<cstdio> #include<cstring> #include<cmath> #include<ctime> #define fuck(x) cout<<#x<<" = "<<x<<endl; #define debug(a,i) cout<<#a<<"["<<i<<"] = "<<a[i]<<endl; #define ls (t<<1) #define rs ((t<<1)+1) using namespace std; typedef long long ll; typedef unsigned long long ull; const int maxn = 100086; const int maxm = 100086; const int inf = 2.1e9; const ll Inf = 999999999999999999; const int mod = 10000007; const double eps = 1e-6; const double pi = acos(-1); ll num[15]; struct Matrix{ ll mp[15][15]; }; Matrix mul(Matrix a,Matrix b,int n){ Matrix ans; for(int i=1;i<=n;i++){ for(int j=1;j<=n;j++){ ans.mp[i][j]=0; for(int k=1;k<=n;k++){ ans.mp[i][j]+=a.mp[i][k]*b.mp[k][j]; } ans.mp[i][j]%=mod; } } return ans; } Matrix q_pow(Matrix a,int b,int n){ Matrix ans; memset(ans.mp,0,sizeof(ans.mp)); for(int i=1;i<=n;i++){ ans.mp[i][i]=1; } while (b){ if(b&1){ ans=mul(ans,a,n); } b>>=1; a=mul(a,a,n); } return ans; } int main() { // ios::sync_with_stdio(false); // freopen("in.txt","r",stdin); int n,m; while(scanf("%d%d",&n,&m)!=EOF){ for(int i=1;i<=n;i++){ scanf("%lld",&num[i]); } Matrix exa; memset(exa.mp,0,sizeof(exa.mp)); int t=0; exa.mp[n+2][n+2]=1; for(int i=1;i<=n+1;i++){ exa.mp[i][1]=10;exa.mp[i][n+2]=1; for(int j=1;j<=t;j++){ exa.mp[i][j+1]=1; } t++; } exa=q_pow(exa,m,n+2); ll ans=0; num[0]=23;num[n+1]=3; for(int i=1;i<=n+2;i++){ ans+=exa.mp[n+1][i]*num[i-1]; ans%=mod; } printf("%lld ",ans); } return 0; }
