题目如下:
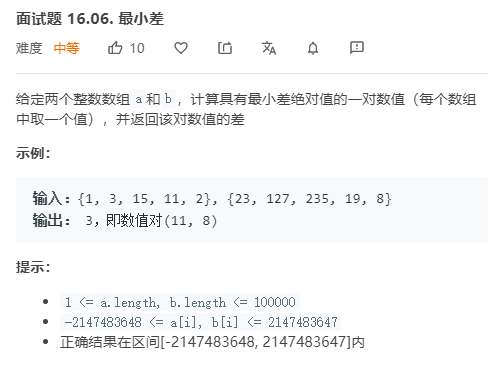
分析:
本题说实话,没什么特殊的技巧,有的只是细节
首先假如我们用暴力枚举两个数组中的所有数对,然后再计算绝对值最小的差值,肯定超时;那么我想了下,我们可以先分别对两个数组按照从小到大的顺序进行排序,然后再使用双指针的方法来计算
算法流程:
1.初始时,我们设置i=0,j=0分别指向两个数组中的第一个元素;
2.然后我们计算a[i]-b[j]的绝对值,如果比当前的最小值还要小,就更新最小值;
3.这里可以减少计算量,我们判断下a[i]和b[j]的大小关系:如果a[i]>b[j],那么如果我们增大i,差值只会越来越大,所以只能增大j;
同理如果a[i]<b[j],那么就增大i
4.最后如果其中一个数组遍历完了,就结束便利。
1 #!/usr/bin/env python 2 # -*- coding: utf-8 -*- 3 """ 4 # @Time : 2020/6/9 9:36 5 6 # @Author : ZFJ 7 8 # @File : 最小差.py 9 10 # @Software: PyCharm 11 """ 12 13 14 class Solution(object): 15 def smallestDifference(self, a, b): 16 """ 17 题解 18 如果暴力枚举两个数组中的所有数对,然后计算绝对值最小的差值,这样显然是会超时的。 19 所以我先分别对两个数组从小到大进行排序,然后用双指针的方法来计算。 20 21 1.初始的时候 i=0,j=0 分别指向两个数组的第一个元素。 22 2.然后计算 a[i]−b[j] 的绝对值,如果比当前最小值还要小,就更新最小值。 23 3.然后判断 a[i]和 b[j]的大小关系。如果 a[i] > b[j],那么如果增大 i,差值只会越来越大,所以只能增大 j。 24 同理如果 a[i] < b[j],那就增大 i。 25 4.最后如果其中一个数组遍历完了就结束遍历。 26 :type a: List[int] 27 :type b: List[int] 28 :rtype: int 29 """ 30 # 首先对a,b进行排序 31 a.sort() 32 b.sort() 33 n, m = len(a), len(b) 34 i, j, res = 0, 0, 2147483647 35 while i < n and j < m: 36 # 使用变量保存最小值 37 res = min(res, abs(a[i] - b[j])) 38 # 如果当前a数组中的值,已经大于b数组中的值,我们只需要b数组继续遍历即可 39 if a[i] > b[j]: 40 j += 1 41 # 否则我们更新a数组中的值 42 else: 43 i += 1 44 return res 45 46 47 A = Solution().smallestDifference(a=[1, 3, 15, 11, 2], b=[23, 127, 235, 19, 8]) 48 print(A)