Codeforces 608 B. Hamming Distance Sum-前缀和

 

B. Hamming Distance Sum

 

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Genos needs your help. He was asked to solve the following programming problem by Saitama:

The length of some string s is denoted |s|. The Hamming distance between two strings s and t of equal length is defined as 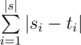, where s_i is the i-th character of s and t_i is the i-th character of t. For example, the Hamming distance between string "0011" and string "0110" is |0 - 0| + |0 - 1| + |1 - 1| + |1 - 0| = 0 + 1 + 0 + 1 = 2.

Given two binary strings a and b, find the sum of the Hamming distances between a and all contiguous substrings of b of length |a|.

Input

The first line of the input contains binary string a (1 ≤ |a| ≤ 200 000).

The second line of the input contains binary string b (|a| ≤ |b| ≤ 200 000).

Both strings are guaranteed to consist of characters '0' and '1' only.

Output

Print a single integer — the sum of Hamming distances between a and all contiguous substrings of b of length |a|.

Examples

Input

01
00111

Output

3

Input

0011
0110

Output

2

Note

For the first sample case, there are four contiguous substrings of b of length |a|: "00", "01", "11", and "11". The distance between "01" and "00" is |0 - 0| + |1 - 0| = 1. The distance between "01" and "01" is |0 - 0| + |1 - 1| = 0. The distance between "01" and "11" is |0 - 1| + |1 - 1| = 1. Last distance counts twice, as there are two occurrences of string "11". The sum of these edit distances is 1 + 0 + 1 + 1 = 3.

The second sample case is described in the statement.

题意就是计算距离，拿数据来说，01和00111，就是01和00，01和01，01和11，01和11，就是下面的依次划取和第一组等长的串来计算，划一次就往后走一个数，反正差不多这个意思，而且！！！第二组的长度一定是>=第一组的长度

代码:

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2*1e5+10;
ll sum[N][2];
char s1[N],s2[N];
int a[N],b[N];

int main(){
    scanf("%s%s",s1+1,s2+1);
    int len1=strlen(s1+1);
    int len2=strlen(s2+1);
    for(int i=1;i<=len1;i++)
        a[i]=s1[i]-'0';
    for(int i=1;i<=len2;i++)
        b[i]=s2[i]-'0';
    for(int i=1;i<=len2;i++){
        for(int j=0;j<2;j++)
            sum[i][j]+=sum[i-1][j];
        sum[i][b[i]]++;
    }
    ll ans=0;
    for(int i=1;i<=len1;i++){
        ans+=sum[len2-len1+i][1-a[i]];
        ans-=sum[i-1][1-a[i]];
    }
    printf("%I64d
",ans);
    return 0;
}