Codeforces 1 C. Ancient Berland Circus-几何数学题+浮点数求gcd ( Codeforces Beta Round #1)

C. Ancient Berland Circus

time limit per test

2 seconds

memory limit per test

64 megabytes

input

standard input

output

standard output

Nowadays all circuses in Berland have a round arena with diameter 13 meters, but in the past things were different.

In Ancient Berland arenas in circuses were shaped as a regular (equiangular) polygon, the size and the number of angles could vary from one circus to another. In each corner of the arena there was a special pillar, and the rope strung between the pillars marked the arena edges.

Recently the scientists from Berland have discovered the remains of the ancient circus arena. They found only three pillars, the others were destroyed by the time.

You are given the coordinates of these three pillars. Find out what is the smallest area that the arena could have.

Input

The input file consists of three lines, each of them contains a pair of numbers –– coordinates of the pillar. Any coordinate doesn't exceed 1000 by absolute value, and is given with at most six digits after decimal point.

Output

Output the smallest possible area of the ancient arena. This number should be accurate to at least 6 digits after the decimal point. It's guaranteed that the number of angles in the optimal polygon is not larger than 100.

Examples

input

Copy

0.000000 0.000000
1.000000 1.000000
0.000000 1.000000

output

Copy

1.00000000

几何数学题，写这个题完全就是记忆一下数学公式。。。

题意就是给你一个正多边形三个点的坐标，三点一定能构成三角形，通过这三个点求所在的多边形的最小面积，肯定是边越少面积越小。

通过三点坐标可以求出三角形的三边长a,b,c；然后求出三角形的面积，然后求出圆的半径。

然后求出三个角(不是三角形的三个角，是圆心对应的三个角)，首先算出余弦，cosC=(a*a+b*b-c*c)/(2*a*b);就是cosC=(r*r+r*r-c*c)/(2*r*r);

然后反余弦函数arccos，代码就是acos(cosC),求出角度C。

求出来三个角之后，找三个角的最大公约数，然后求出这最大公约数的三角形对应的三角形的面积，然后总的圆心角2*PI/最大公约数，就是一共的个数，乘起来就可以了。

三角形的面积：海伦公式 s=sqrt(p*(p-a)*(p-b)*(p-c))，p=(a+b+c)/2;

又因为三角形面积s=1/2*a*b*sinC.

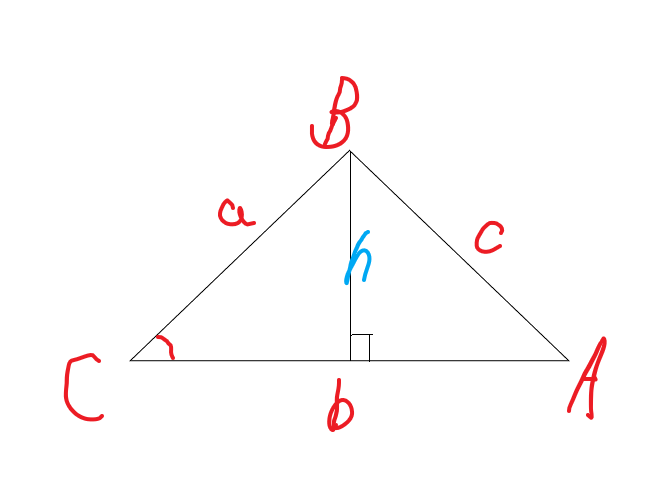
因为a/sinA=b/sinB=c/sinC=2*r,所以sinC=c/(2*r)，所以s=a*b*c/(4*r).

好多啊，不想写了。。。直接贴一下别人的题解。

传送门:

CodeForces-1C-Ancient Berland Circus

这个题eps开的太小会错，一开始写的1e-9，wa了，改成1e-4过了，精确度太高过不了。。。

 

代码:

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int maxn=1e5+10;
const double PI=acos(-1.0);
const double eps=1e-4;

struct node{
    double x,y;
};

double len(node a,node b)//求边长
{
    return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}

double acos(double a,double b,double c)//求反余弦
{
    return acos((a*a+b*b-c*c)/(2*a*b));
}

double fgcd(double a,double b)//求浮点数的gcd
{
    if(b<eps) return a;
    return fgcd(b,fmod(a,b));
}

int main()
{
    node A,B,C;
    cin>>A.x>>A.y;cin>>B.x>>B.y;cin>>C.x>>C.y;
    double a=len(B,C),b=len(A,C),c=len(A,B);
    //cout<<a<<" "<<b<<" "<<c<<endl;
    double p=(a+b+c)/2;
    double s=sqrt(p*(p-a)*(p-b)*(p-c));//海伦公式求三角形面积
    double r=a*b*c/(4*s);//求圆的半径
    double AA=acos(r,r,a),BB=acos(r,r,b),CC=2*PI-AA-BB;//求角度
    //cout<<AA<<" "<<BB<<" "<<CC<<endl;
    double angle=fgcd(AA,fgcd(BB,CC));//求最大公约数的角度
    //cout<<angle<<endl;
    double sr=(r*r*sin(angle))/2;//求每一小块的面积
    double ans=sr*2*PI/angle;
    printf("%.6f
",ans);
}