关于线段树,其实我一开始也是很懵的,但看久了也就习惯了。
以下是我对线段树的一点理解,写得不好,也请各位看官见谅。
搜狗定义:线段树(Segment Tree)是一种二叉搜索树,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。
定义还是很显然的。
那么线段树都能做些什么呢?
在n个数中有m个询问,询问如下:
1.把q这个数改成v O(logn);
2.求在1~n这个区间的和.
接下来我们讲原理(当然原理也是我自己的理解,可能不是正解,但我想,线段树这个东西大概就是这样的吧)
首先看图
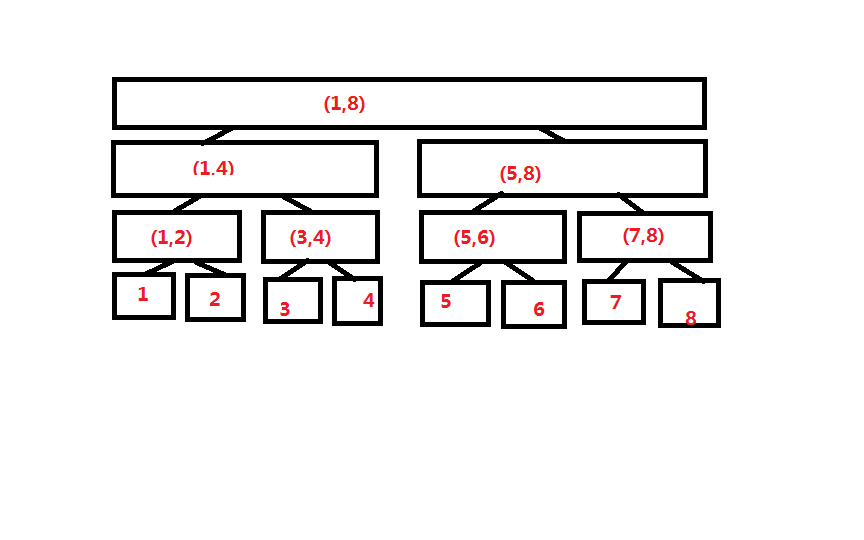
下面我们将原理
1.它是用“二进制”存储的
什么是“二进制”存储?
众所周知,用二的倍数可以表示所有的数
例:13=1+4+8;
(具体原理请参考二进制和十进制的转换)
那么线段树也是这样:
如:我们要查找(2,5)这个区间,那它就是2+(3,4)+5所代表的数(区间和)
2.它是“二分查找”(当然不是严格意义上的)
二分查找不再赘述
例:当我们要把6这个位置上所在的数改为★,那我们一定是这样查找的:
(1,8)->(5,8)->(5,6)->(6)->(★)
那么怎么实现呢?我大概总结了一下几个步骤:
1.建立线段树
2.查找位置+动作
具体代码如下
int a[maxn];//每个数的值 int sum[maxn*4];//区间和 void update(int rt) { sum[rt]=sum[rt*2]+sum[rt*2+1];//前缀和思想 } void build(int l,int r,int rt)//建立树,左孩子,右孩子,根 { if(l==r) { sum[rt]=a[l]; return ;//边界 } int m=(l+r)/2; build(1,m,rt*2); build(m+1,r,rt*2+1); update(rt);//合并两个儿子 }
//如果不理解左孩子右孩子为什么要那样写的,看这里:
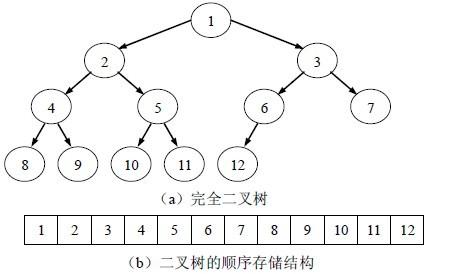
以根节点为例:(1)
左孩子:1*2=2;
右孩子:1*2+1=3;
这样就能保证树在数组里存满且不重复。
void modify(int l,int r,int rt,int p,int v)//将p的位置上的数改为v { if(l==r) { sum[rt]=v; return ;//找到这个数了,改值。当然我们也会顺便把与它相关的所有值都改掉 } int m=(l+r)/2; if(p<=m) modify(1,m,rt*2,p,v); else modify(m+1,r,rt*2+1,p,v);//二分查找 update(rt); } int query(int l.int r,int rt,int nowl,int nowr)//询问(nowl,nowr)这个区间和 { if(nowl<=1&&r<=nowr)//边界 return sum[rt]; int m=(l+r)/2; int ans=0; if(nowl<=m)ans+=query(1,m,rt*2,nowl,nowr); if(m<nowr)ans+=query(m+1,r,rt*2+1,nowl,nowr);//查找求和 return ans; }
这是两次询问。
主函数的话就依据情况调用这三个函数就好了
那我要讲的,大概就是这些了。
byebey!^_^