可持久化数据结构（线段树，trie树）

1.可持久化线段树

• 又称主席树，因为发明这一算法的人的名字缩写为HJT。
• 主席树可以储存各个历史状态，如果用普通线段树，每个状态都是 4n 的，内存和时间开销极大，而主席树通过动态开点，先继承上一状态的左右儿子节点指针，再进行修改，每次修改的时间和空间都可以优化到 (log n) 级别。
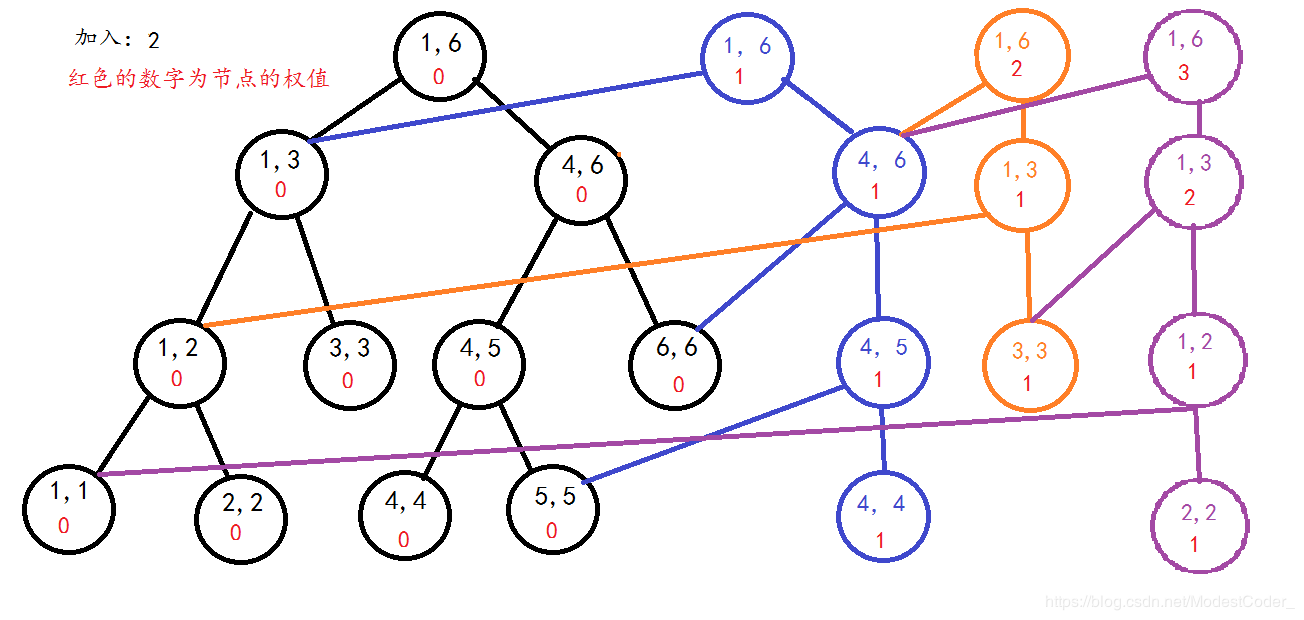
• 通过下图主席树的结构进行一下理解，黑色部分是普通的线段树，有颜色部分为每次的修改。

• 看一下实现过程。

#define lson t[rt].l, l, mid
#define rson t[rt].r, mid + 1, r

void Change(int &rt, int l, int r, int x) {
    t[++tot] = t[rt];//继承上一状态
    rt = tot;//注意rt是引用变量，可以更改对上一层进行更改
    ++t[rt].s;//计数++
    if (l == r) return;//递归边界
    int mid = l+r >> 1;
    x <= mid ? Change(lson, x) : Change(rson, x);
}

例题1

• P3834 【模板】可持久化线段树 2（主席树）
  • 「区间第k小」给定 n 个整数构成的序列 a，将对于指定的闭区间 [l,r] 查询其区间内的第 k 小值。
• 建议离散化，不离散化直接维护-1e9到1e9也可以，只是这样时间和空间都会比较大。

Code

#include <cstdio>
#include <algorithm>
#define lson t[rt].l, l, mid
#define rson t[rt].r, mid + 1, r
using namespace std;
const int N = 2e5 + 5;
struct Tree{
    int s, l, r;
}t[N*20];
int a[N], h[N], n, m, Q, root[N], tot;
void Change(int &rt, int l, int r, int x) {
    t[++tot] = t[rt]; rt = tot;
    ++t[rt].s;
    if (l == r) return;
    int mid = l+r >> 1;
    x <= mid ? Change(lson, x) : Change(rson, x);
}
int Ask(int lrt, int rt, int l, int r, int k) {//在线段树中二分查找答案
    if (l == r) return l;
    int mid = l+r >> 1;
    int s = t[t[rt].l].s - t[t[lrt].l].s;//这里有些类似于前缀和
    if (s >= k) return Ask(t[lrt].l, lson, k);
    else return Ask(t[lrt].r, rson, k - s);
}
int main() {
    scanf("%d%d", &n, &Q);
    for (int i = 1; i <= n; ++i)    
        scanf("%d", &a[i]), h[i] = a[i];
    sort(h + 1, h + n + 1);
    m = unique(h + 1, h + n + 1) - h - 1;//离散化
    root[0] = ++tot;
    for (int i = 1; i <= n; ++i) {
        int x = lower_bound(h + 1, h + m + 1, a[i]) - h;
        Change(root[i] = root[i-1], 1, m, x);
    }
    while (Q--) {
        int l, r, k;
        scanf("%d%d%d", &l, &r, &k);
        printf("%d
", h[Ask(root[l-1], root[r], 1, m, k)]);
    }
    return 0;
}

例题2

• P2633 Count on a tree
  • 「树上第k小」给定一棵 n 个节点的树，每个点有一个权值。有 m 个询问，每次给你 u,v,k，你需要回答 (u ext{ xor last}) 和 v 这两个节点间第 k 小的点权。 其中 last 是上一个询问的答案，定义其初始为 0
• x 到 y 路径上的和等于 (s_x+s_y-s_{lca}-s_{fa[lca]})，其实和上一道题区别不大

Code

#include <cstdio>
#include <algorithm>
#define lson t[rt].l, l, mid
#define rson t[rt].r, mid + 1, r
using namespace std;
const int N = 1e5 + 5;
struct Side {
    int t, next;
}e[N<<1];
int head[N], tot;
void Add(int x, int y) {
    e[++tot] = (Side) {y, head[x]};
    head[x] = tot;
}
struct Tree {
    int l, r, s;
}t[N*20];
int n, m, a[N], b[N], f[N][21], d[N], trc, root[N], last;
void Change(int &rt, int l, int r, int x) {
    t[++trc] = t[rt]; rt = trc;
    ++t[rt].s;
    if (l == r) return;
    int mid = l+r >> 1;
    x <= mid ? Change(lson, x) : Change(rson, x);
}
int Ask(int x, int y, int lca, int flca, int l, int r, int k) {
    if (l == r) return l;
    int mid = l+r >> 1, s;
    s = t[t[x].l].s + t[t[y].l].s - t[t[lca].l].s - t[t[flca].l].s;
    if (s >= k) return Ask(t[x].l, t[y].l, t[lca].l, t[flca].l, l, mid, k);
    else return Ask(t[x].r, t[y].r, t[lca].r, t[flca].r, mid + 1, r, k - s);
}
void Dfs(int x) {
    int num = lower_bound(b + 1, b + b[0] + 1, a[x]) - b;
    Change(root[x] = root[f[x][0]], 1, b[0], num);
    d[x] = d[f[x][0]] + 1;
    for (int i = head[x]; i; i = e[i].next) {
        int y = e[i].t;
        if (y == f[x][0]) continue;
        f[y][0] = x;
        Dfs(y);
    }
}
int Jump(int x, int k) {
    int i = 0;
    while (k) {
        if (k & 1) x = f[x][i];
        k >>= 1; ++i;
    }
    return x;
}
int Lca(int x, int y) {
    if (d[x] < d[y]) swap(x, y);
    for (int i = 0, k = d[x] - d[y]; k; k >>= 1, ++i)
        if (k & 1) x = f[x][i];
    if (x == y) return x;
    for (int i = 20; i >= 0; --i)
        if (f[x][i] != f[y][i])
            x = f[x][i], y = f[y][i];
    return f[x][0];
}
int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++i)
        scanf("%d", &a[i]), b[i] = a[i];
    sort(b + 1, b + n + 1);
    b[0] = unique(b + 1, b + n + 1) - b - 1;
    for (int i = 1; i < n; ++i) {
        int x, y;
        scanf("%d%d", &x, &y);
        Add(x, y); Add(y, x);
    }
    root[0] = ++trc;
    Dfs(1);
    for (int i = 1; i <= 20; ++i)
        for (int x = 1; x <= n; ++x)
            f[x][i] = f[f[x][i-1]][i-1];//倍增Lca预处理
    while (m--) {
        int x, y, k;
        scanf("%d%d%d", &x, &y, &k);
        x ^= last;
        int lca = Lca(x, y);
        //k = d[x] + d[y] - d[lca] * 2 + 1 - k + 1;
        last = b[Ask(root[x], root[y], root[lca], root[f[lca][0]], 1, b[0], k)];
        printf("%d
", last);
    }
    return 0;
}

2.可持久化Trie树

• 学会了主席树，其实这个就是一个道理了。
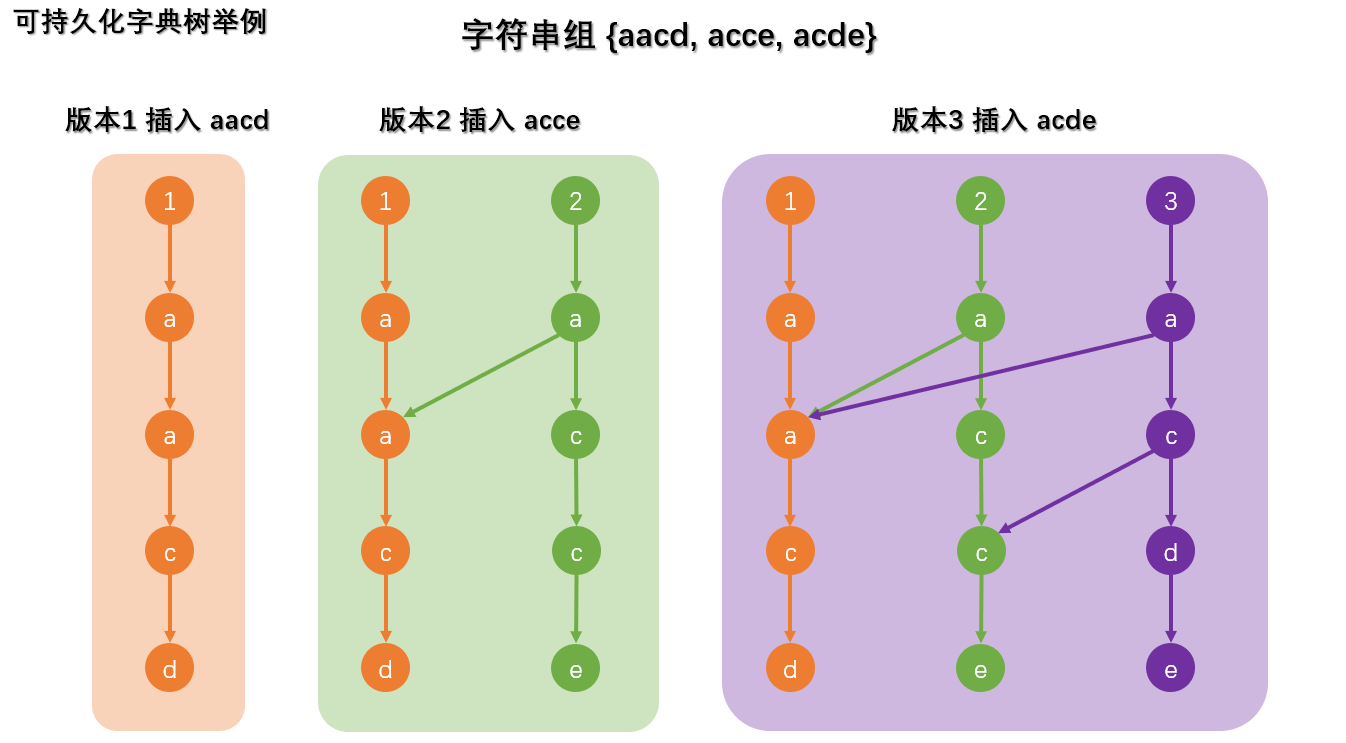
• 看下面这张图，长的和主席树还是挺像的。

例题

• P4735 最大异或和
  • 给 n 个数，每次操作在最后添加一个数或在 [l,r] 中选一个数 p，使得 p 到结尾的异或和异或上 x 的值最大。
• 看到异或就很大概率是Trie树了。

Code

#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 6e5 + 5;
int n, m, t[N*24][2], tot, s[N], b[N*24], root[N];
void Insert(int p, int lp, int k, int i) {
    if (k < 0) return b[p] = i, void();
    bool y = s[i]>>k & 1;
    if (lp) t[p][y^1] = t[lp][y^1];
    t[p][y] = ++tot;
    Insert(t[p][y], t[lp][y], k - 1, i);
    b[p] = max(b[t[p][0]], b[t[p][1]]);
}
int Ask(int p, int lim, int k, int x) {
    if (k < 0) return s[b[p]] ^ x;
    bool y = x>>k & 1;
    if (b[t[p][y^1]] >= lim) 
        return Ask(t[p][y^1], lim, k - 1, x);
    return Ask(t[p][y], lim, k - 1, x);
}
int main() {
    scanf("%d%d", &n, &m);
    b[0] = -1;
    root[0] = ++tot;
    Insert(root[0], 0, 23, 0);
    for (int i = 1; i <= n; ++i) {
        scanf("%d", &s[i]);
        s[i] ^= s[i-1];
        root[i] = ++tot;
        Insert(root[i], root[i-1], 23, i);
    }
    while (m--) {
        char od;
        scanf(" %c", &od);
        if (od == 'A') {
            scanf("%d", &s[++n]);
            s[n] ^= s[n-1];
            root[n] = ++tot;
            Insert(root[n], root[n-1], 23, n);
        }
        else {
            int l, r, x;
            scanf("%d%d%d", &l, &r, &x);
            printf("%d
", Ask(root[r-1], l-1, 23, s[n] ^ x));
        }
    }
    return 0;
}