最长公共子序列
目录
接下来我们来学习一下最长公共序列。
定义
最长公共子序列,英文缩写为LCS(Longest Common Subsequence)。其定义是:一个序列S,如果分别是两个或多个已知序列的子序列,且是所有符合此条件序列中最长的,则S称为已知序列的最长公共子序列。
问题引进
首先我们引进一个问题:在一个计算机词典中,用户想要找一个单词,
fish,但是用户不小心把单词拼写错误了,拼出了hish......这可怎么办。词典中当然没有hish这个单词,但是我们有fish,finish等单词,我们是不是应该去找这个单词呢?

对于这个问题,我们该.....怎么解决呢???
思想构成
简述思想
- 对于这个问题.....我们不妨,可以通过比较他们的字符串,从而得到用户所需要的一个单词。就好比如说,
fish,finish这两个单词都有ish这个字段,但用户输入的单词(hish)长度为4,那么....我们不可能去匹配finish这个单词,因为超出了用户拼写单词的最长长度..... - 简而言之.....我们得从
fish这个单词中匹配我们需要的单词。接下来.....便是怎么匹配的问题了。
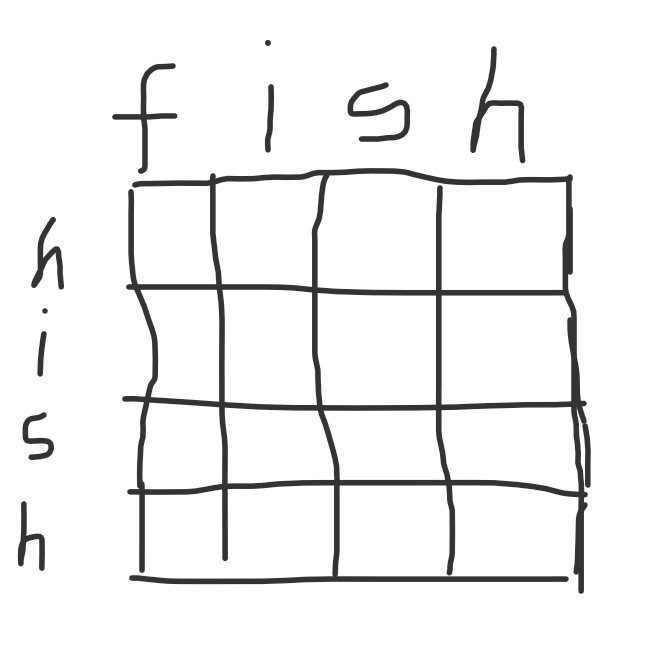
匹配思想
- 对于这个我们刚刚的简述的内容,我们边可以进行匹配了......(这是废话....)
- 匹配的思路大概是这样的:
我们可以从第一个字符开始比,然后比对到最后一个字符。一一进行比较,一直到最后我们的所有的字符都完成,最后统计哪些字符串是比较接近的,然后我们进行输出....
- 对于上面的这个思路....只能说,可以实行但是复杂度很高,基本上接近了O( n2 )...我们是否有另一种思路去做这个问题?
动态规划
了解一下动态规划:
- 动态规划可以帮助你在给定的约束条件下找到最优解。在背包问题中,我们可以在给定的背包容量的情况下,偷到价值最高的商品。
- 在问题可分解为彼此独立且离散的子问题,那么我们可以想一下这个大的问题能不能使用动态规划去解决。
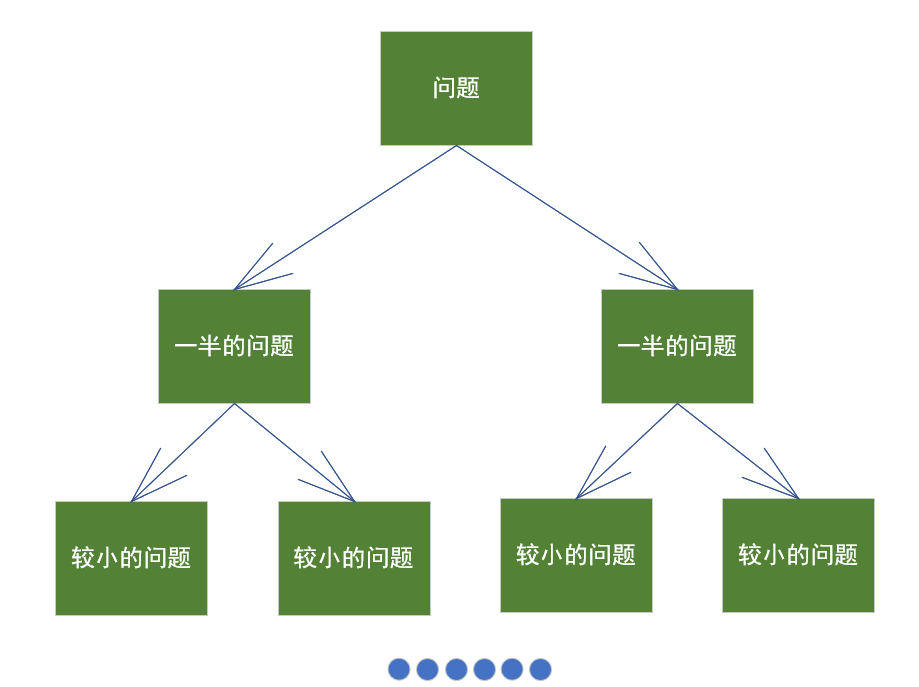
我们再来学习一些小tips:
- 每种动态规划解决方案都涉及网格。
- 单元格中的值通常就是你要优化的值。
- 每个单元格都是一个子问题,因此你应该考虑如何将问题分成子问题,这有助于找出网络的坐标轴。
根据刚刚所说的一些动态规划的思想和tips,我们如果需要利用动态规划的话,我们得把这个问题分解成若干个子问题....
就好比如,我们找fish,输入了hish,那么我们得比较h和fish的匹配程度,然后还得分别比较i,s,h这几个,最后在进行合并,那么我们就可以求得fish和hish单词的匹配度。
这就是一个巫术......很难,我们想不出任何的思路。为什么不用费曼算法来解决呢?步骤如下:
- 将问题写下来
- 好好思考
- 将答案写下来

哈哈,不逗了,接下来我们来解决LCS(最长公共子序列)问题
解决问题
为了解决LCS问题,我们需要把原问题分解成若干个子问题,所以需要刻画LCS的特征。
- 设A="a0,a1,...,am",B="b0,b1,...,bn",且Z="z0,z1,...,zk",为他们的最长公共子序列。他们有如下的性质
- 如果am=bn,则zk=am=bn,且"z0,z1,...,z(k-1)"是"a0,a1,...,a(m-1)"和"b0,b1,...,b(n-1)"的一个最长公共子序列
- 如果am!=bn,则若zk!=am,蕴含"z0,z1,...,zk"是"a0,a1,...,a(m-1)"和"b0,b1,...,bn"的一个最长公共子序列
- 如果am!=bn,则若zk!=bn,蕴含"z0,z1,...,zk"是"a0,a1,...,am"和"b0,b1,...,b(n-1)"的一个最长公共子序列
进行一系列的递归以及代入操作,我们得到了以下的递归公式。我们使用一个矩阵来进行运算......
| 0 i==0||j==0
c[ i, j ]| c[i-1][j-1]+1 i,j>0&&xi==yi
| max{c[i][j-1],c[i-1][j]} i,j>0&&xi!=yi
请看图示:
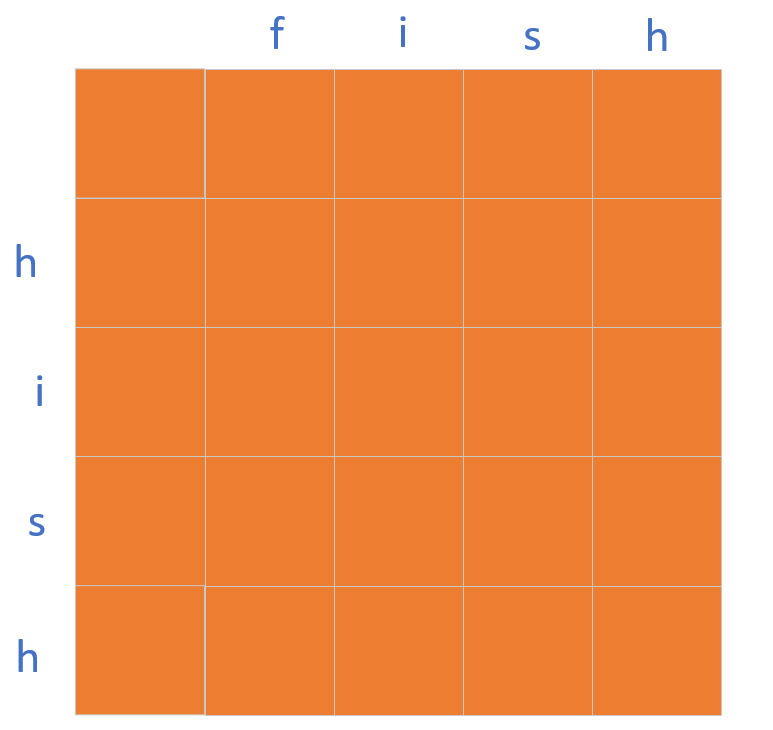
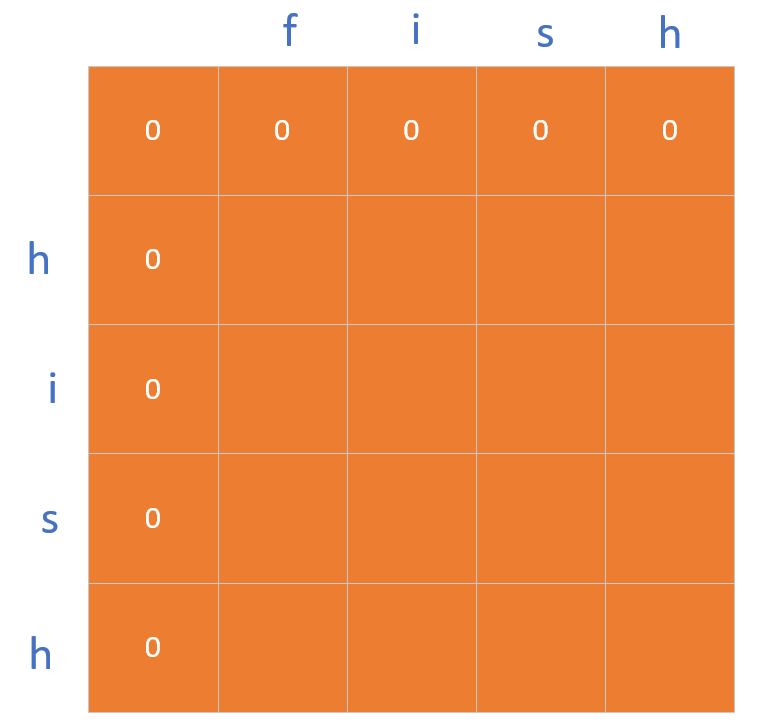
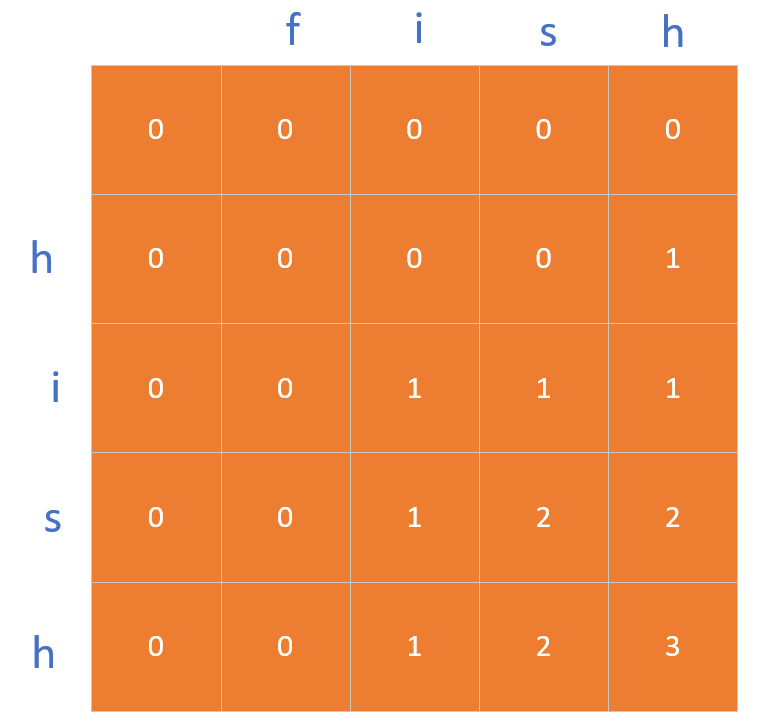
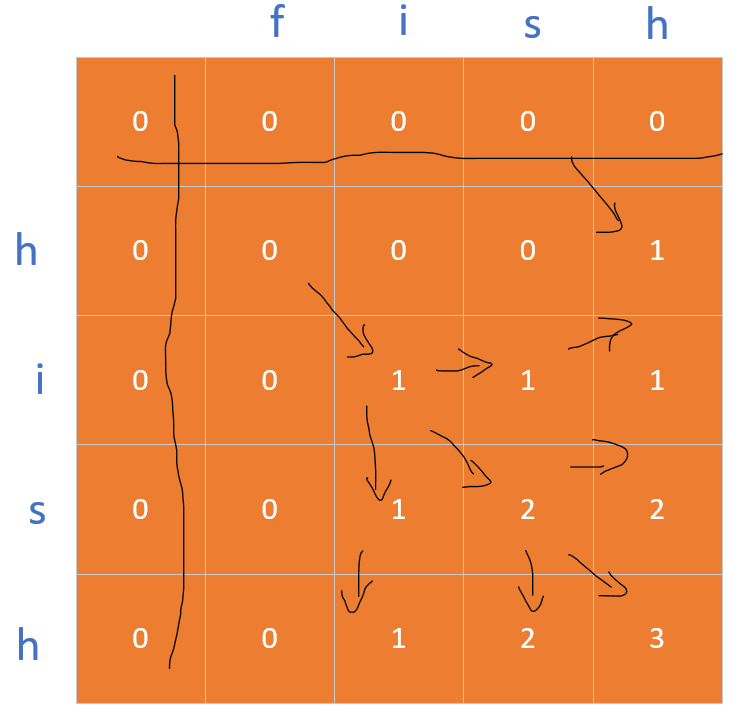
好了,以上便是最长字段的讲解了.......
在完成这个存储数的矩阵之后,最后一个元素的值便是我们需要求的的字符串的长度。这是运行图:
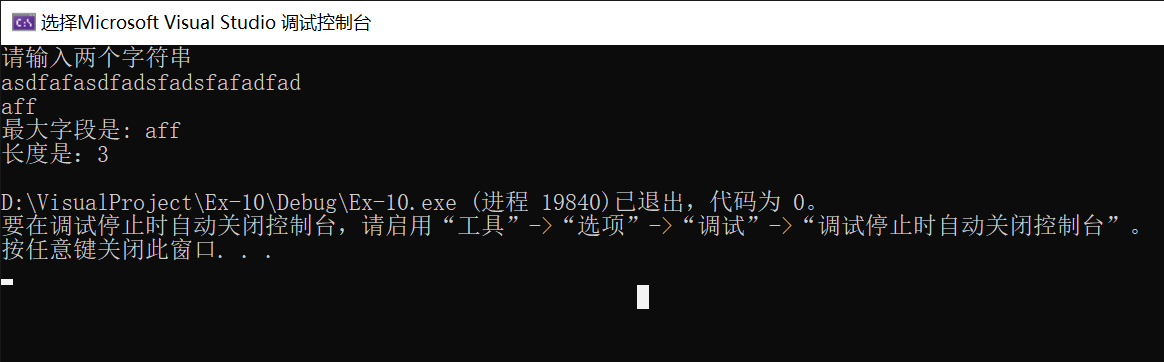
接下来便是代码部分
#include<iostream>
#include<vector>
#include<cstdlib>
#include<string>
#include<stack>
using namespace std;
string MaxSegments(string& str1, string& str2);
string Process(int a, int b, string& str1, string& str2);
void Display(vector<vector<int>>& pos);
void Display(vector<vector<string>>& pos);
int main()
{
string str1, str2, pos;
cout << "请输入两个字符串" << endl;
cin >> str1 >> str2;
pos=MaxSegments(str1, str2);
cout << "最大字段是: " << pos << endl;
cout << "长度是:" << pos.size() << endl;
return 0;
}
string MaxSegments(string &str1,string &str2)
{
//根据大小来开放空间
int a = str1.size();
int b = str2.size();
string pos;
if (a > b)//当传进来的字符串1的长度比第二个长
{
pos = Process(a, b, str1, str2);
}
else//比第二个短
{
pos = Process(b, a, str2, str1);
}
return pos;
}
string Process(int a, int b, string& str1, string& str2)
{
vector<vector<int>>Pair(a+1, vector<int>(b+1, 0));//用来存储最大长度
vector<vector<string>>Graph(a+1, vector<string>(b+1, "0"));//用来存储走的路径
stack<char>ans;
string pos;
for (int i = 0; i < a+1; i++)
{
for (int j = 0; j < b+1; j++)
{
if (i == 0 || j == 0)//这是条件方程
{
Pair[i][j] = 0;
Graph[i][j] = "0";
}
else if ((i > 0 || j > 0) && (str1[i-1] == str2[j-1]))
{
Pair[i][j] = Pair[i - 1][j - 1] + 1;
Graph[i][j] = "↖";
}
else
{
if (Pair[i - 1][j] > Pair[i][j - 1])
{
Pair[i][j] = Pair[i - 1][j];
Graph[i][j] = "↑";
}
else
{
Pair[i][j] = Pair[i][j - 1];
Graph[i][j] = "←";
}
}
}
}//经过之后,可以找到最长字串的个数了
//Display(Pair);//测试的时候显示路径
//Display(Graph);
while (Graph[a][b] != "0")
{
if (Graph[a][b] == "↖")
{
ans.push(str1[a-1]);
a--, b--;
}
else if (Graph[a][b] == "↑")
{
a--;
}
else if (Graph[a][b] == "←")
{
b--;
}
}
while (!ans.empty())
{
pos.push_back(ans.top());
ans.pop();
}
return pos;
}
void Display(vector<vector<int>>& pos)
{
for (int i = 0; i < pos.size(); i++)
{
for (int j = 0; j < pos[0].size(); j++)
{
cout << pos[i][j] << " ";
}
cout << endl;
}
}
void Display(vector<vector<string>>& pos)
{
for (int i = 0; i < pos.size(); i++)
{
for (int j = 0; j < pos[0].size(); j++)
{
cout << pos[i][j] << " ";
}
cout << endl;
}
}
参考书籍《算法导论》、《算法图解》、百度百科