Codeforces contest 856 D(树形DP,树剖)

超链接:http://codeforces.com/contest/856/problem/D

题意就是给你一棵树,和一些树上的链,每个链有一个权值,要求求一个不相交链的集合,使得权值最大.

两条链相交定义为这两条链有公共点.

那么这题非常的难,于是我不会做......

咳咳咳.......

我于是就学了一发正解.

f[i]表示在以i为根的子树中的答案(仅能包含在完全在子树内的链)

那么把链集中压到两端点lca的vector里去.

设sum[i]=sigma(f[son[i]])

很好理解

f[i]=max(sum[i],对每条在i的vector里的链的可能答案);

那么怎么计算后者呢?

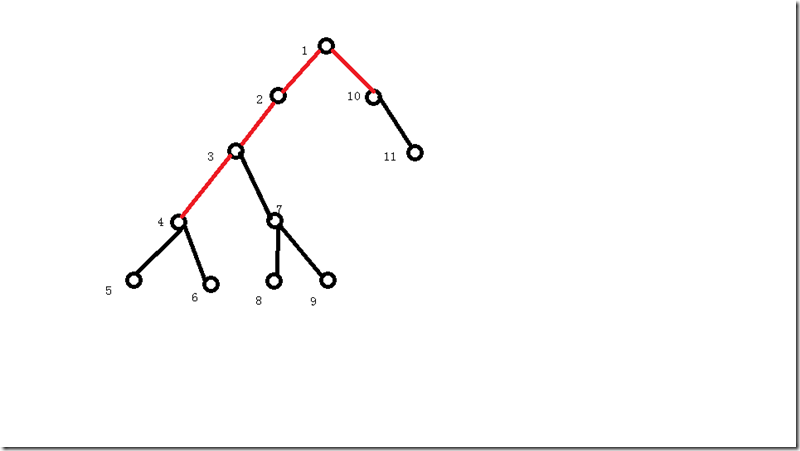
如图:

现在要更新f[1]

红色的链为考虑的链,那么它的可能答案就是f[5]+f[6]+f[7]+f[11]+1

变形一下就是sum[4]+sum[3]-f[4]+sum[2]-f[3]+sum[1]-f[2]+sum[10]+sum[1]-f[10]-sum[1]+1

sum[1]加了两遍,所以要减去一次.

那么你就可以根据这个写出DP了

复杂度是O(n+m)(Tanjan LCA)+O(n*链的期望长度)(树形DP)

但是这样只能过随机数据,不能过hack数据.

于是考虑树剖优化.

维护contribution[i]表示从这条重链底端到它的sigma(sum[i]-f[son[i]])(此处son[i]表示重儿子)

每次跳的时候直接到链顶.

再乱计算一波就可以了.

贴上我的乱计算代码:

int calc(int i,int x){ int y=u[i],z=v[i],res=sum[y]+sum[z]; while (top[y]!=top[x]) res+=contribution[top[y]]-contribution[y]+sum[fa[top[y]]]-dp[top[y]],y=fa[top[y]]; res+=contribution[x]-contribution[y]; while (top[z]!=top[x]) res+=contribution[top[z]]-contribution[z]+sum[fa[top[z]]]-dp[top[z]],z=fa[top[z]]; res+=contribution[x]-contribution[z]; return res-sum[x]+money[i]; }i是链的编号,top是链顶,money是权值.然后这题就可以过了.悲伤的是我竟然写了一个tanjan lca 其实可以沿用树剖.

代码:

#include<bits/stdc++.h>
using namespace std;
const int N=200010;
int n,m,x,y,k,ancestor[N],fa[N],fi[N],u[N],v[N],sum[N],dp[N],ne[N<<1],b[N<<1],money[N],sz[N],top[N],son[N],contribution[N];
vector<pair<int,int> >g[N];
vector<int>w[N];
inline int read() {
    char ch=getchar(); int x=0;
    while(ch<'0'||ch>'9') ch=getchar();
    while('0'<=ch&&ch<='9'){
        x=x*10+ch-'0';
        ch=getchar();
    }
    return x;
}
inline void add(int x,int y){b[++k]=y; ne[k]=fi[x]; fi[x]=k;}
inline int ask(int x){return x==ancestor[x]?x:ancestor[x]=ask(ancestor[x]);}
inline int ask2(int x){return x==top[x]?x:top[x]=ask2(top[x]);}
inline void dfs(int x){
    sz[x]=1;
    for (int j=fi[x]; j; j=ne[j]){
        fa[b[j]]=x;
        dfs(b[j]);
        ancestor[b[j]]=x;
        sz[x]+=sz[b[j]];
        if (sz[b[j]]>sz[son[x]]) son[x]=b[j];
    }
    top[son[x]]=x;
    for (vector<pair<int,int> >::iterator it=g[x].begin(); it!=g[x].end(); it++)
        if (it->second==1||fa[it->second]) w[ask(it->second)].push_back(it->first);
}
int calc(int i,int x){
    int y=u[i],z=v[i],res=sum[y]+sum[z];
    while (top[y]!=top[x]) res+=contribution[top[y]]-contribution[y]+sum[fa[top[y]]]-dp[top[y]],y=fa[top[y]];
    res+=contribution[x]-contribution[y];
    while (top[z]!=top[x]) res+=contribution[top[z]]-contribution[z]+sum[fa[top[z]]]-dp[top[z]],z=fa[top[z]];
    res+=contribution[x]-contribution[z];
    return res-sum[x]+money[i];
}
void getans(int x){
    for (int j=fi[x]; j; j=ne[j]){
        getans(b[j]);
        sum[x]+=dp[b[j]];
    }
    dp[x]=sum[x];
    contribution[x]=contribution[son[x]]+sum[x]-dp[son[x]];
    for (vector<int>::iterator it=w[x].begin(); it!=w[x].end(); it++) dp[x]=max(dp[x],calc(*it,x));
}
int main(){
    n=read(); m=read();
    for (int i=2; i<=n; i++) add(read(),i);
    for (int i=1; i<=m; i++){
        u[i]=read(); v[i]=read(); money[i]=read();
        g[u[i]].push_back(make_pair(i,v[i]));
        g[v[i]].push_back(make_pair(i,u[i]));
    }
    for (int i=1; i<=n; i++) ancestor[i]=top[i]=i;
    dfs(1);
    for (int i=1; i<=n; i++) ask2(i);
    for (int i=1; i<=n; i++) w[i].erase(unique(w[i].begin(),w[i].end()),w[i].end());
    getans(1);
    printf("%d",dp[1]);
}

不知道是不是我写炸了,当两个端点有父子关系或相等时,tajan lca 会把一个lca压入vector两次.于是有奇怪的话

for (int i=1; i<=n; i++) w[i].erase(unique(w[i].begin(),w[i].end()),w[i].end());

纯属作死.

当然不加这句话也没事,只会让程序变慢而已.