Description
公元2089年6月4日,在经历了17年零3个月的漫长旅行后,“格纳格鲁一号”载人火箭返回舱终于安全着陆。此枚火箭由美国国家航空航天局(NASA)研制发射,行经火星、金星、土卫六、木卫二、谷神星、“张衡星”等23颗太阳系星球,并最终在小行星“杰森星”探寻到了地外生命。宇航员在“杰森星”地表岩层下45.70米位置发现一批珍贵的活体生命样本,并将其带回检测。在带回的活体样本中,最吸引人的当属这些来自外星的千足虫了。这些虫子身躯纤长,身体分为若干节。受到触碰时,会将身体卷曲成圆环形,间隔一段时间后才会复原活动。
有趣的还不止如此。研究人员发现,这些虫子的足并不像地球千足虫成对出现、总共偶数条——它们每节身体下方都有着不定数量的足,但足的总数一定是奇数条!虽然从外观难以区分二者,但通过统计足的数目,科学家们就能根据奇偶性判断出千足虫所属的星球。
作为J国派去NASA的秘密间谍,你希望参加这次研究活动以掌握进一步的情报,而NASA选拔的研究人员都是最优秀的科学家。于是NASA局长Charles Bolden出了一道难题来检测你的实力:
现在你面前摆有1…N编号的N只千足虫,你的任务是鉴定每只虫子所属的星球,但不允许亲自去数它们的足。Charles每次会在这N只千足虫中选定若干只放入“昆虫点足机”(the Insect Feet Counter, IFC)中,“点足机”会自动统计出其内所有昆虫足数之和。Charles会将这个和数mod 2的结果反馈给你,同时告诉你一开始放入机器中的是哪几只虫子。他的这种统计操作总共进行M次,而你应当尽早得出鉴定结果。
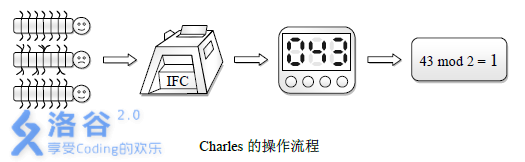
假如在第K次统计结束后,现有数据就足以确定每只虫子的身份,你就还应将这个K反馈给Charles,此时若K<M,则表明那后M-K次统计并非必须的。
如果根据所有M次统计数据还是无法确定每只虫子身份,你也要跟Charles讲明:就目前数据会存在多个解。
Input
第一行是两个正整数N, M。
接下来M行,按顺序给出Charles这M次使用“点足机”的统计结果。每行包含一个“01”串和一个数字,用一个空格隔开。“01”串按位依次表示每只虫子是否被放入机器:如果第i个字符是“0”则代表编号为i的虫子未被放入,“1”则代表已被放入。后面跟的数字是统计的昆虫足数mod 2的结果。
由于NASA的实验机器精确无误,保证前后数据不会自相矛盾。即给定数据一定有解。
Output
在给定数据存在唯一解时有N+1行,第一行输出一个不超过M的正整数K,表明在第K次统计结束后就可以确定唯一解;接下来N行依次回答每只千足虫的身份,若是奇数条足则输出“?y7M#”(火星文),偶数条足输出“Earth”。如果输入数据存在多解,输出“Cannot Determine”。
所有输出均不含引号,输出时请注意大小写。
Hint
对于20%的数据,满足N=M≤20;
对于40%的数据,满足N=M≤500;
对于70%的数据,满足N≤500,M≤1,000;
对于100%的数据,满足N≤1,000,M≤2,000。
Solution
显然要高斯消元解异或方程组。
这题 (N) 有点大,可以用 (bitset) 优化。
最开始想的是二分找这个满足要求的最小的 (K),无奈复杂度过不去。
考虑高斯消元的过程,假设当前在消第 (i) 列,第 (j) 行,那么一定是从第 (j) 行向下找一个最小的 (p) ,满足 (a[p][i]=1)。这里的最小的就已经满足题目要求了,不必要在二分了。也就是说,每次 (swap) 时取一个 (max) 即可。
其他就跟高斯消元一模一样了。
Code
#include<cstdio>
#include<cctype>
#include<bitset>
#define N 1005
#define M 2005
#define bi std::bitset<N>
#define max(A,B) ((A)>(B)?(A):(B))
int n,m;
bi a[M];
int getint(){
int x=0;char ch=getchar();
while(!isdigit(ch)) ch=getchar();
while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
return x;
}
void swap(bi &x,bi &y){bi t=x;x=y;y=t;}
signed main(){
n=getint(),m=getint();
for(int i=1;i<=m;i++){
int x;
for(int j=1;j<=n;j++){
scanf("%1d",&x);
a[i][j]=x;
}
x=getint();a[i][n+1]=x;
}
int now,ans=0;
for(int i=1;i<=n;i++){
now=i;
while(now<=m and !a[now][i])
now++;
if(now==m+1){
printf("Cannot Determine");
return 0;
}
ans=max(ans,now);
if(now!=i)
swap(a[now],a[i]);
for(int j=1;j<=m;j++){
if(j==i)
continue;
if(!a[j][i])
continue;
a[j]^=a[i];
}
}
printf("%d
",ans);
for(int i=1;i<=n;i++){
if(a[i][n+1])
printf("?y7M#
");
else
printf("Earth
");
}
return 0;
}