梯度下降法的python代码实现(多元线性回归最小化损失函数)
1、梯度下降法主要用来最小化损失函数,是一种比较常用的最优化方法,其具体包含了以下两种不同的方式:批量梯度下降法(沿着梯度变化最快的方向进行搜索最小值)和随机梯度下降法(主要随机梯度下降,通过迭代运算,收敛到最小值)
2、随机梯度与批量梯度计算是梯度下降的两种比较常用的方法,随机梯度下降法计算效率较高,不过不太稳定,对于批量梯度下降法,虽然计算速度较慢,但是计算方向稳定,它一定会朝着我们最优化的方向不断的进行靠近计算,结合以上两种方法便可以得到小批量梯度下降法。
3、随机的机器学习算法具有以下的优点:
(1)有助于跳出局部最优解
(2)更快地运行速度
(3)机器学习领域许多算法都要用到随机的特点,比如随机搜索,随机森林等。
1)批量梯度下降法

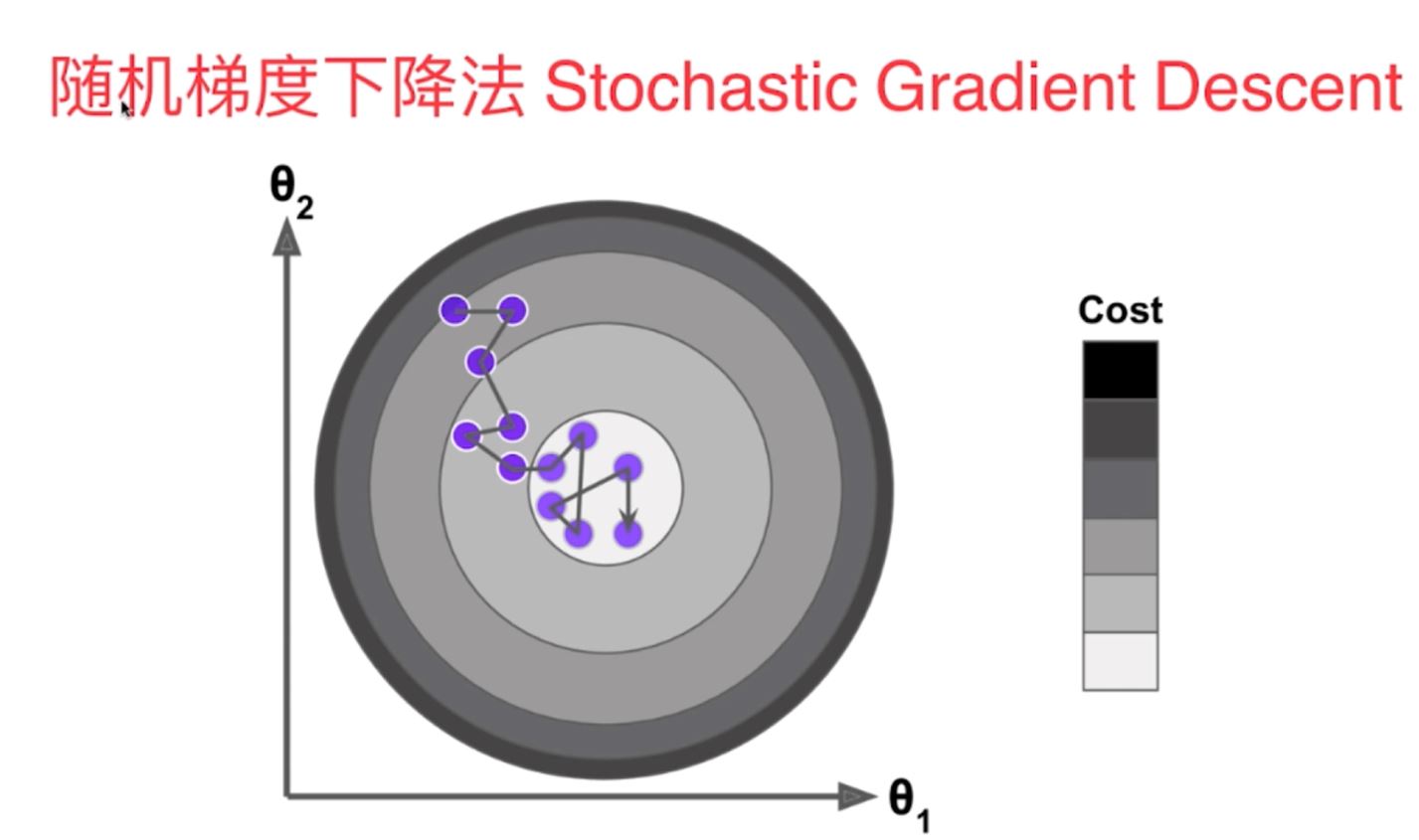
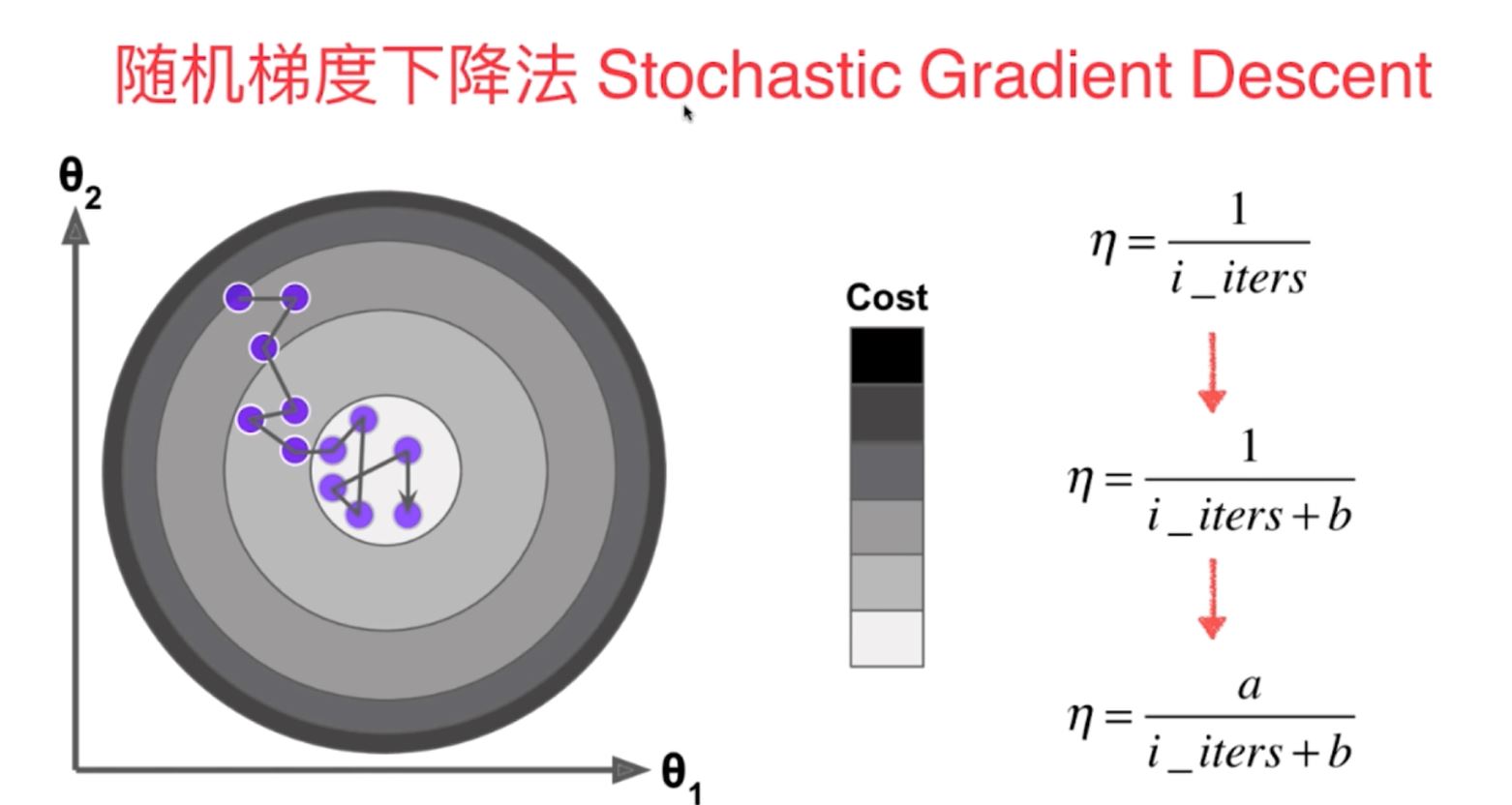
2)随机梯度下降法(学习率eta随着训练次数的增大而不断减小,采用了模拟退火的原理,不再是定值)
多元线性回归中的梯度下降法的向量化的数学计算原理:


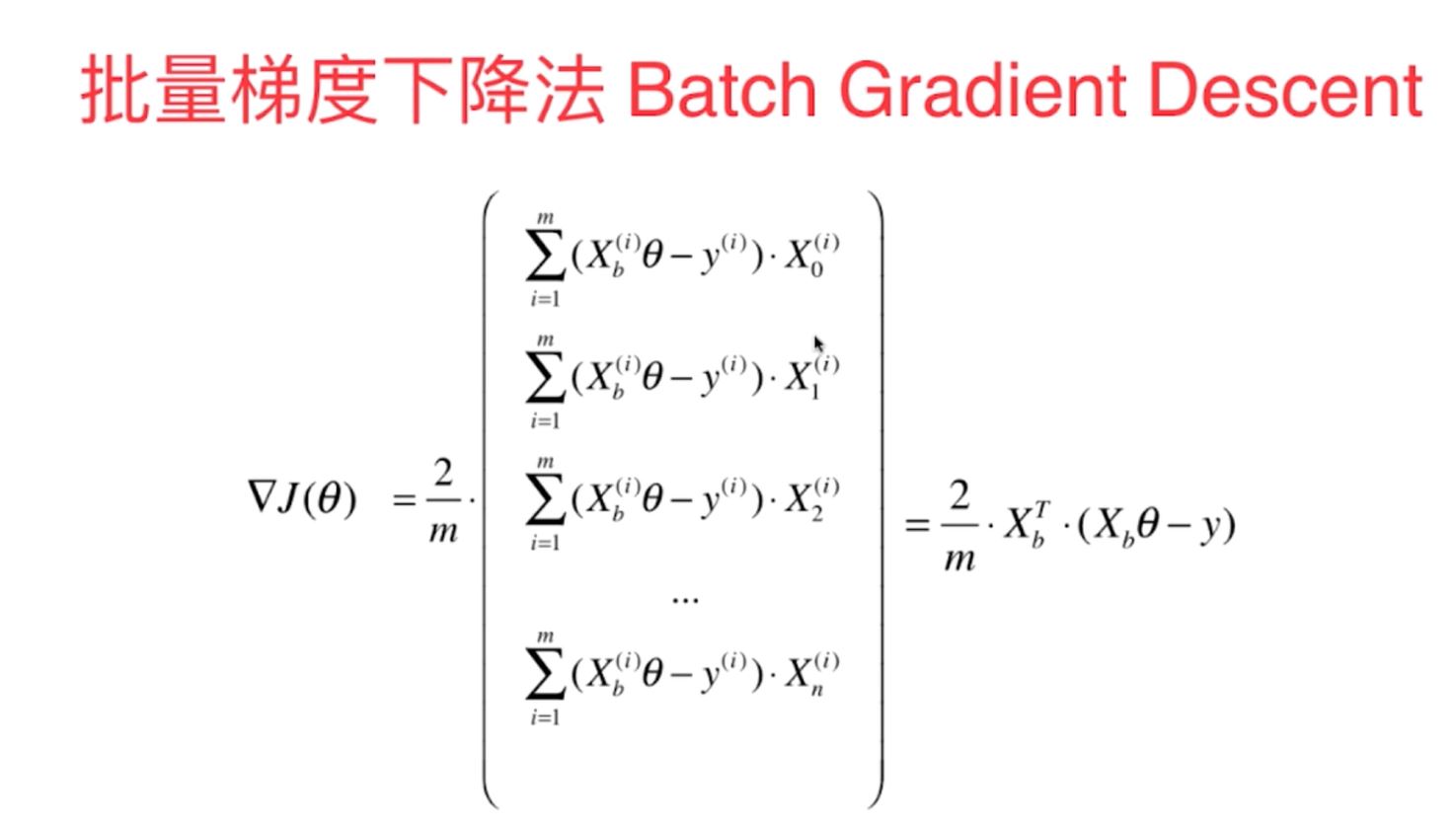

以上两种梯度下降法方法的python代码原理函数实现如下:
(1)批量梯度下降法:
#多元线性回归中使用梯度下降法来求得损失函数的最小值
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(666)
x=np.random.random(size=100)
y=x*3.0+4+np.random.normal(size=100)
X=x.reshape(-1,1)
print(X)
print(x.shape)
print(y.shape)
plt.scatter(x,y)
plt.show()
print(X)
print(len(X))
#1使用梯度下降法训练
def J1(theta,x_b,y):
return np.sum((y-x_b.dot(theta))**2)/len(x_b)
def DJ2(theta,x_b,y):
res=np.empty(len(theta))
res[0]=np.sum(x_b.dot(theta)-y)
for i in range(1,len(theta)):
res[i]=np.sum((x_b.dot(theta)-y).dot(x_b[:,i]))
return res*2/len(x_b)
def DJ1(theta, x_b, y):
return x_b.T.dot(x_b.dot(theta)-y)*2/len(y)
def gradient_descent1(x_b,y,eta,theta_initial,erro=1e-8, n=1e4):
theta=theta_initial
i=0
while i<n:
gradient = DJ1(theta,x_b,y)
last_theta = theta
theta = theta - gradient * eta
if (abs(J1(theta,x_b,y) - J1(last_theta,x_b,y))) < erro:
break
i+=1
return theta
x_b=np.hstack([np.ones((len(X),1)),X])
print(x_b)
theta0=np.zeros(x_b.shape[1])
eta=0.1
theta1=gradient_descent1(x_b,y,eta,theta0)
print(theta1)
from sklearn.linear_model import LinearRegression
l=LinearRegression()
l.fit(X,y)
print(l.coef_)
print(l.intercept_)
#2随机梯度下降法的函数原理代码(多元线性回归为例):
#1-1写出损失函数的表达式子
def J_SGD(theta, x_b, y):
return np.sum((y - x_b.dot(theta)) ** 2) / len(x_b)
#1-2写出梯度胡表达式
def DJ_SGD(theta, x_b_i, y_i):
return x_b_i.T.dot(x_b_i.dot(theta)-y_i)*2
#1-3写出SGD随机梯度的函数形式
def SGD(x_b, y, theta_initial, n):(这里的n便是遍历和随机的总次数)——随机方式1
t0=5
t1=50
def learning_rate(t):(计算eta学习率)
return t0/(t+t1) #计算学习率eta的表达式,需要随着次数的增大而不断的减小
theta = theta_initial #定义初始化的点(列阵)
for i1 in range(n): #采用不断增加次数迭代计算的方式来进行相关的计算
rand_i=np.random.randint(len(x_b)) #生成随机的索引值,计算随机梯度
gradient = DJ_SGD(theta, x_b[rand_i], y[rand_i])
theta = theta - gradient *learning_rate(i1)
return theta
def SGD1(x_b, y, theta_initial, n,t0=5,t1=50):(这里的n便是遍历次数,每次对每一个索引进行一遍随机迭代)——随机方式2(更加有效)
def learning_rate(t):
return t0/(t+t1) #计算学习率eta的表达式,需要随着次数的增大而不断的减小
theta = theta_initial #定义初始化的点(列阵)
m=len(x_b)
for i1 in range(n): #采用不断增加次数迭代计算的方式来进行相关的计算
index1=np.random.permutation(m)
x_b_new=x_b[index1]
y_new=y[index1]
for k in range(m):
gradient = DJ_SGD(theta, x_b_new[k], y_new[k])
theta = theta - gradient *learning_rate(i1*m+k)
return theta
np.random.seed(666)
x=np.random.random(size=100)
y=x*3.0+4+np.random.normal(size=100)
X=x.reshape(-1,1)
print(X)
print(x.shape)
print(y.shape)
plt.scatter(x,y)
plt.show()
print(X)
print(len(X))
#1-4初始化数据x,y以及定义超参数theta0,迭代次数n
x_b=np.hstack([np.ones((len(X),1)),X])
print(x_b)
theta0=np.zeros(x_b.shape[1])
theta1=SGD(x_b,y,theta0,100000)
print(theta1)