最小二乘法则是一种统计学习优化技术,它的目标是最小化误差平方之和来作为目标J(θ)J(θ),从而找到最优模型。
7. SciPy最小二乘法
最小二乘法则是一种统计学习优化技术,它的目标是最小化误差平方之和来作为目标J(θ),从而找到最优模型。

1、线性最小二乘法
假设真实的模型是y=2x+1,我们有一组数据(xi,yi)共100个,看能否基于这100个数据找出xi和yi的线性关系方程y=2x+1?我们可以通过以下几步来完成。
1).首先是通过程序构造出100个(xi,yi)数据。
xi = x + np.random.normal(0, 0.05, 100)
yi = 1 + 2 * xi + np.random.normal(0, 0.05, 100)
2).接下来给出模型f(x)=a+bx的矩阵A,由于有100个观测(xi,yi)的数据,那么就有:
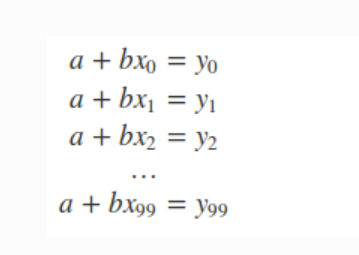
将以上式子写成如下矩阵的形式:

A = np.vstack([xi**0, xi**1])
AT即100×2的那个矩阵
3).调用scipy.linalg.lstsq传入AT和观测值里的yii即程序里的yi变量即可求得f(x)=a+bx里的a和b。a和b记录在lstsq函数的第一个返回值里。
sol, r, rank, s = la.lstsq(A.T, yi)
4). scipy.linalg.lstsq的第一个返回值sol共有两个值,sol[0]即是估计出来的f(x)=a+bx里a,sol[1]代表f(x)=a+bx里b。因此f(x)为:
y_fit = sol[0] + sol[1] * x
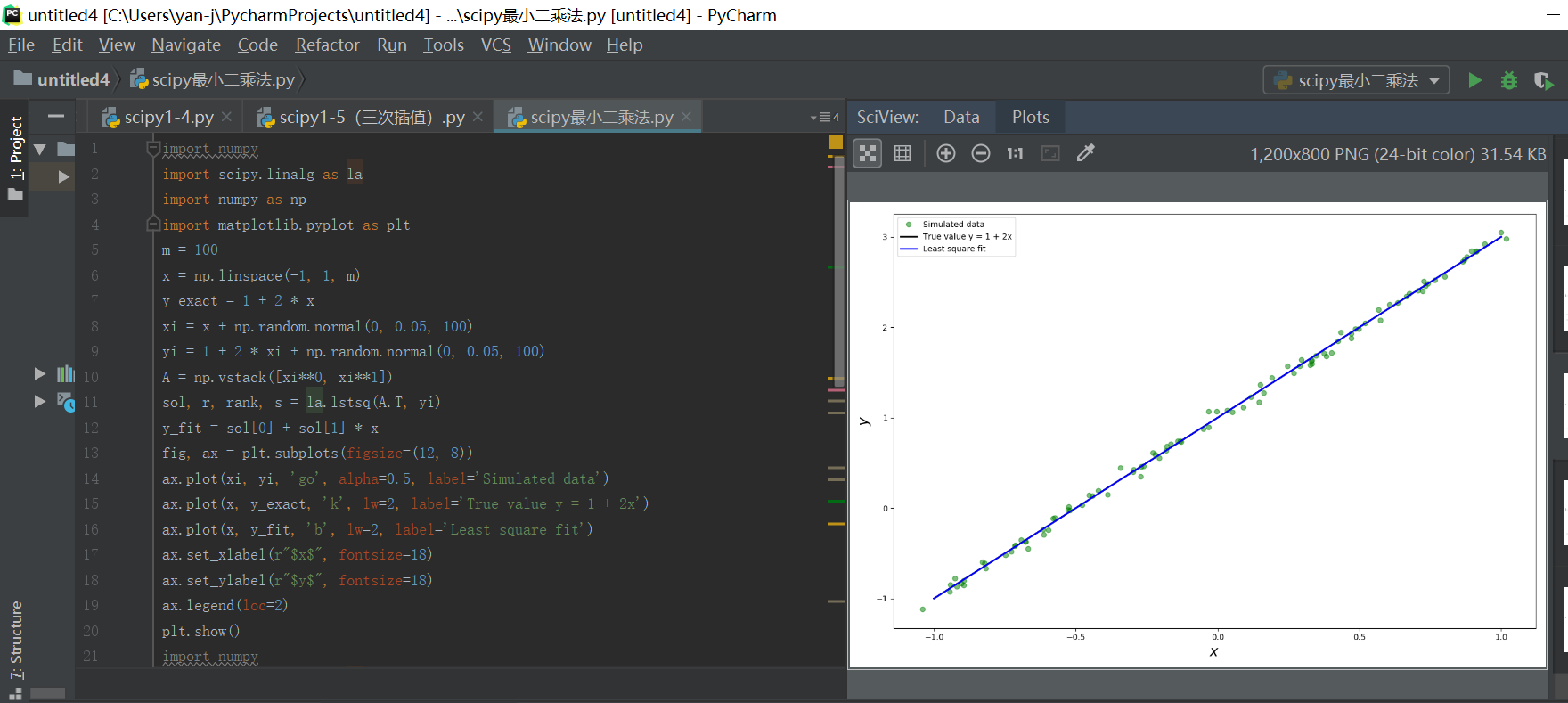
至此找到了这100个(xi,yi)的模型方程。从print sol语句的输出结果可以看出数据还是比较接近y=2x+1的。
完整的代码如下所示:
import scipy.linalg as la
import numpy as np
import matplotlib.pyplot as plt
m = 100
x = np.linspace(-1, 1, m)
y_exact = 1 + 2 * x
xi = x + np.random.normal(0, 0.05, 100)
yi = 1 + 2 * xi + np.random.normal(0, 0.05, 100)
A = np.vstack([xi**0, xi**1])
sol, r, rank, s = la.lstsq(A.T, yi) #求取各个系数大小
y_fit = sol[0] + sol[1] * x
fig, ax = plt.subplots(figsize=(12, 8))
ax.plot(xi, yi, 'go', alpha=0.5, label='Simulated data')
ax.plot(x, y_exact, 'k', lw=2, label='True value y = 1 + 2x')
ax.plot(x, y_fit, 'b', lw=2, label='Least square fit')
ax.set_xlabel("x", fontsize=18)
ax.set_ylabel(”y", fontsize=18)
ax.legend(loc=2) #设置曲线标注位置
plt.show()
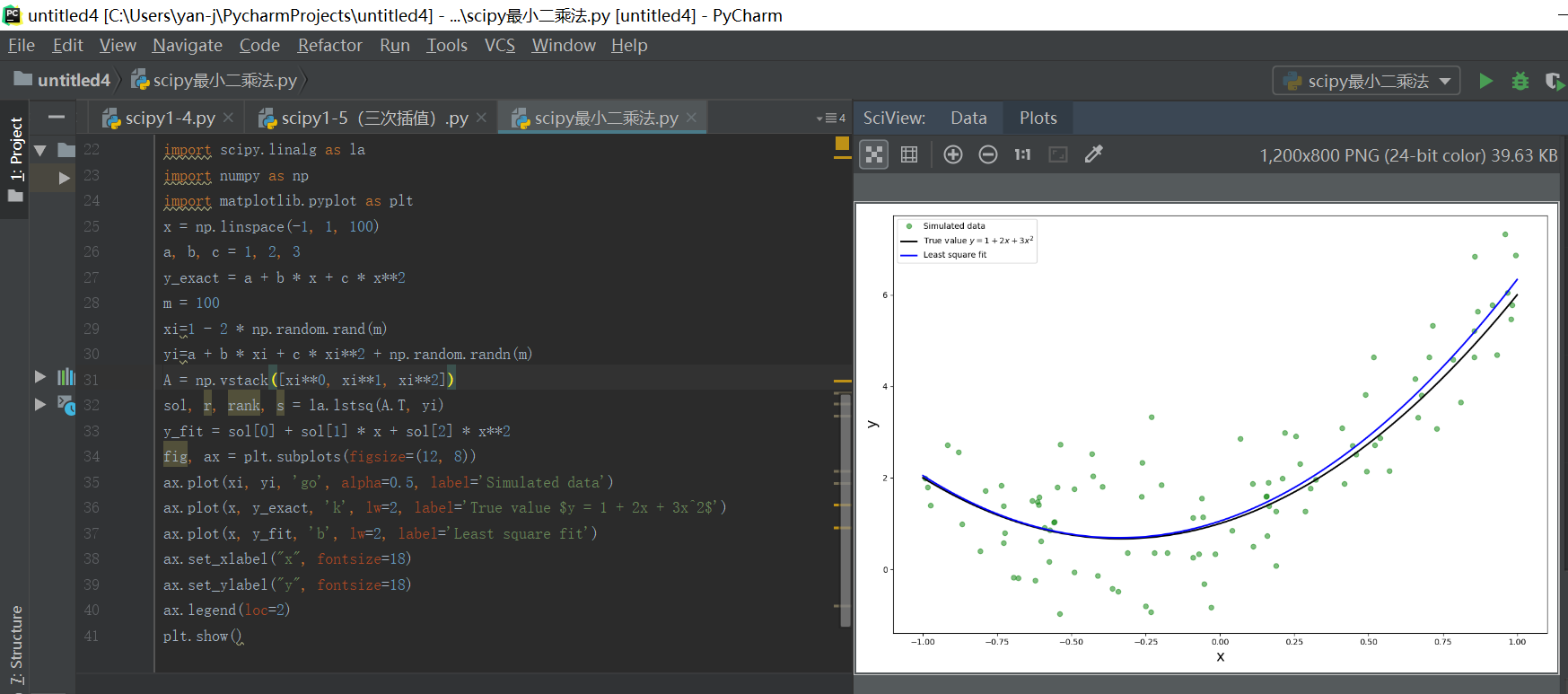
2、二次函数最小二乘法
这个程序和上面的程序差不多,只不过模型变成了f(xi)=a+bx+cx2f(xi)=a+bx+cx2了而已,请自己分析分析。
完整程序如下:
import scipy.linalg as la
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(-1, 1, 100)
a, b, c = 1, 2, 3
y_exact = a + b * x + c * x**2
m = 100
xi=1 - 2 * np.random.rand(m)
yi=a + b * xi + c * xi**2 + np.random.randn(m)
A = np.vstack([xi**0, xi**1, xi**2])
sol, r, rank, s = la.lstsq(A.T, yi)
y_fit = sol[0] + sol[1] * x + sol[2] * x**2
fig, ax = plt.subplots(figsize=(12, 4))
ax.plot(xi, yi, 'go', alpha=0.5, label='Simulated data')
ax.plot(x, y_exact, 'k', lw=2, label='True value $y = 1 + 2x + 3x^2$')
ax.plot(x, y_fit, 'b', lw=2, label='Least square fit')
ax.set_xlabel("x", fontsize=18)
ax.set_ylabel("y", fontsize=18)
ax.legend(loc=2)
plt.show()
具体结果展示如下: