题目描述
有一个无向图G,每个点有个权值,每条边有一个颜色。这个无向图满足以下两个条件:
-
对于任意节点连出去的边中,相同颜色的边不超过两条。
-
图中不存在同色的环,同色的环指相同颜色的边构成的环。
在这个图上,你要支持以下三种操作:
-
修改一个节点的权值。
-
修改一条边的颜色。
-
查询由颜色c的边构成的图中,所有可能在节点u到节点v之间的简单路径上的节点的权值的最大值。
输入输出格式
输入格式:
输入文件network.in的第一行包含四个正整数N, M, C, K,其中N为节点个数,M为边数,C为边的颜色数,K为操作数。
接下来N行,每行一个正整数vi,为节点i的权值。
之后M行,每行三个正整数u, v, w,为一条连接节点u和节点v的边,颜色为w。满足1 ≤ u, v ≤ N,0 ≤ w < C,保证u ≠ v,且任意两个节点之间最多存在一条边(无论颜色)。
最后K行,每行表示一个操作。每行的第一个整数k表示操作类型。
-
k = 0为修改节点权值操作,之后两个正整数x和y,表示将节点x的权值vx修改为y。
-
k = 1为修改边的颜色操作,之后三个正整数u, v和w,表示将连接节点u和节点v的边的颜色修改为颜色w。满足0 ≤ w < C。
-
k = 2为查询操作,之后三个正整数c, u和v,表示查询所有可能在节点u到节点v之间的由颜色c构成的简单路径上的节点的权值的最大值。如果不存在u和v之间不存在由颜色c构成的路径,那么输出“-1”。
输出格式:
输出文件network.out包含若干行,每行输出一个对应的信息。
-
对于修改节点权值操作,不需要输出信息。
-
对于修改边的颜色操作,按以下几类输出:
a) 若不存在连接节点u和节点v的边,输出“No such edge.”。
b) 若修改后不满足条件1,不修改边的颜色,并输出“Error 1.”。
c) 若修改后不满足条件2,不修改边的颜色,并输出“Error 2.”。
d) 其他情况,成功修改边的颜色,并输出“Success.”。
输出满足条件的第一条信息即可,即若同时满足b和c,则只需要输出“Error 1.”。
- 对于查询操作,直接输出一个整数。
输入输出样例
4 5 2 7 1 2 3 4 1 2 0 1 3 1 2 3 0 2 4 1 3 4 0 2 0 1 4 1 1 2 1 1 4 3 1 2 0 1 4 1 2 3 1 0 2 5 2 1 1 4
4 Success. Error 2. -1 Error 1. 5
说明
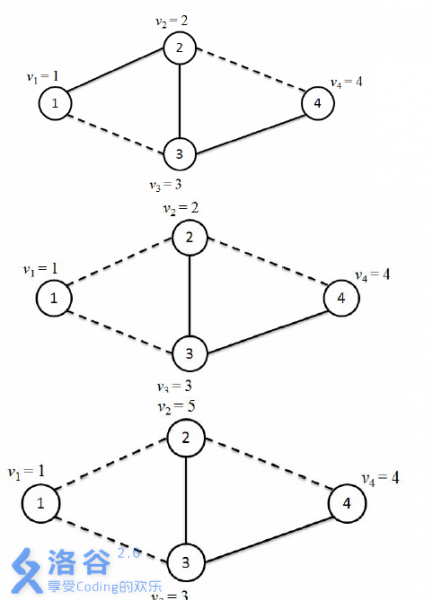
颜色0为实线的边,颜色1为虚线的边,
由颜色0构成的从节点1到节点4的路径有1 – 2 – 4,故max{v1, v2, v4} = max{ 1, 2, 4 } = 4。
将连接节点1和节点2的边修改为颜色1,修改成功,输出“Success.”
将连接节点4和节点3的边修改为颜色1,由于修改后会使得存在由颜色1构成的环( 1 – 2 – 4 – 3 – 1 ),不满足条件2,故不修改,并输出“Error 2”。
不存在颜色0构成的从节点1到节点4的边,输出“-1”。
将连接节点2和节点3的边修改为颜色1,由于修改后节点2的连出去的颜色为1的边有3条,故不满足条件1,故不修改,并输出“Error 1.”。
将节点2的权值修改为5。
由颜色1构成的从节点1到节点4的路径有 1 – 2 – 4,故max{v1, v2, v4} = max{ 1, 5, 4 } = 5。
【数据规模】
对于30%的数据:N ≤ 1000,M ≤ 10000,C ≤ 10,K ≤ 1000。
另有20%的数据:N ≤ 10000,M ≤ 100000,C = 1,K ≤ 100000。
对于100%的数据:N ≤ 10000,M ≤ 100000,C ≤ 10,K ≤ 100000。
注:题面复制于洛谷。
题解Here!
我本来一看到颜色数,$woc$,又一道置换群的题,吓得不敢做。。。
直到今天我补完了$Polya$定理的最后一点内容,回头来看这题。
心想这下会做了吧。。。
然后这个$flag$在$3s$之后被推翻了。。。
这$TM$不是$LCT$的沙茶题么???
感觉自己就是个沙茶。。。
根据题目,我们可以发现我们要维护几条链,还要断来断去,连来连去的。。。
当然$LCT$!
注意到颜色数最多只有$10$中,所以直接开$10$颗$LCT$就好辣!
操作$0$好做,直接暴力对每个颜色的链中的$x$修改就好。
操作$2$也好做,用$findroot(x)$判连通,直接查询就好。
这两个是$LCT$基本操作了。
来看操作$1$。
我直接用$STL$里的$map$来求$u,v$之间的边的颜色。
注意我的颜色数为了方便,是$[1,c]$的。
$STL$大法好!
如果颜色为$0$,或者$u==v$(题目活坑。。。),说明没有边,直接输出$No such edge.$(有句点!)
对于限制$1$,我们对于每个颜色开一个$degree[x]$记录$x$连接的边有多少条,然后大力特判就好。
对于限制$2$,用$findroot(x)$判断连通即可。
其他情况就先$cut(u,v)$,再$link(u,v)$即可。不要忘了维护$degree[x]$哦!
记得特判新的边的颜色是否和原来的颜色相同,这种情况直接输出$Success.$。
然后就是一大堆细节问题了,这个只能看代码,我也没有辨法啊。。。
附代码:
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<map>
#define MAXN 10010
using namespace std;
map<int,int> colour[MAXN];
int n,m,c,q;
int val[MAXN];
int top=0,stack[MAXN];
inline int read(){
int date=0,w=1;char c=0;
while(c<'0'||c>'9'){if(c=='-')w=-1;c=getchar();}
while(c>='0'&&c<='9'){date=date*10+c-'0';c=getchar();}
return date*w;
}
struct LCT{
int degree[MAXN];
struct Link_Cut_Tree{
int son[2];
int f,v,flag;
}a[MAXN];
inline bool isroot(int rt){
return a[a[rt].f].son[0]!=rt&&a[a[rt].f].son[1]!=rt;
}
inline void pushup(int rt){
if(!rt)return;
a[rt].v=max(val[rt],max(a[a[rt].son[0]].v,a[a[rt].son[1]].v));
}
inline void pushdown(int rt){
if(!rt||!a[rt].flag)return;
a[a[rt].son[0]].flag^=1;a[a[rt].son[1]].flag^=1;a[rt].flag^=1;
swap(a[rt].son[0],a[rt].son[1]);
}
inline void turn(int rt){
int x=a[rt].f,y=a[x].f,k=a[x].son[0]==rt?1:0;
if(!isroot(x)){
if(a[y].son[0]==x)a[y].son[0]=rt;
else a[y].son[1]=rt;
}
a[rt].f=y;a[x].f=rt;a[a[rt].son[k]].f=x;
a[x].son[k^1]=a[rt].son[k];a[rt].son[k]=x;
pushup(x);pushup(rt);
}
void splay(int rt){
top=0;
stack[++top]=rt;
for(int i=rt;!isroot(i);i=a[i].f)stack[++top]=a[i].f;
while(top)pushdown(stack[top--]);
while(!isroot(rt)){
int x=a[rt].f,y=a[x].f;
if(!isroot(x)){
if((a[y].son[0]==x)^(a[x].son[0]==rt))turn(rt);
else turn(x);
}
turn(rt);
}
}
inline void access(int rt){
for(int i=0;rt;i=rt,rt=a[rt].f){
splay(rt);
a[rt].son[1]=i;
pushup(rt);
}
}
inline void makeroot(int rt){access(rt);splay(rt);a[rt].flag^=1;}
int findroot(int rt){
access(rt);splay(rt);
while(a[rt].son[0])rt=a[rt].son[0];
return rt;
}
inline void split(int x,int y){makeroot(x);access(y);splay(y);}
inline void link(int x,int y){makeroot(x);a[x].f=y;}
inline void cut(int x,int y){
split(x,y);
if(a[y].son[0]==x&&a[x].f==y&&!a[x].son[1])a[x].f=a[y].son[0]=0;
}
inline void update(int rt,int k){access(rt);splay(rt);val[rt]=k;pushup(rt);}
inline int query(int x,int y){split(x,y);return a[y].v;}
inline bool check(int x,int y){
if(findroot(x)!=findroot(y))return false;
return true;
}
}tree[11];
void work(){
int f,x,y,k;
while(q--){
f=read();
if(f==0){
x=read();k=read();
for(int i=1;i<=c;i++)tree[i].update(x,k);
}
else if(f==1){
x=read();y=read();k=read()+1;
int w=colour[x][y];
if(w==k)printf("Success.
");
else if(!w||x==y)printf("No such edge.
");
else if(tree[k].degree[x]==2||tree[k].degree[y]==2)printf("Error 1.
");
else if(tree[k].check(x,y))printf("Error 2.
");
else{
colour[x][y]=k;
tree[w].cut(x,y);
tree[w].degree[x]--;tree[w].degree[y]--;
tree[k].link(x,y);
tree[k].degree[x]++;tree[k].degree[y]++;
printf("Success.
");
}
}
else{
k=read()+1;x=read();y=read();
if(!tree[k].check(x,y))printf("-1
");
else printf("%d
",tree[k].query(x,y));
}
}
}
void init(){
int u,v,w;
n=read();m=read();c=read();q=read();
for(int i=1;i<=n;i++)val[i]=read();
for(int i=1;i<=m;i++){
u=read();v=read();w=read()+1;
colour[u][v]=colour[v][u]=w;
tree[w].degree[u]++;tree[w].degree[v]++;
tree[w].link(u,v);
}
}
int main(){
init();
work();
return 0;
}