先看一道题目:洛谷P3959 宝藏
第一想法是最小生成树,但是并不对,只能过40%的数据。
n<=12?想起了TSP/状压DP。
(不知道TSP问题戳这里。)
用 f[u][i] 表示从 u 出发,点是否可以到达的状态为 i 。
(因为计算 f[u][i] 时只用 f[u] 里的状态计算,可以算用了滚动数组,省略一维的 u )。
然后枚举点 j,k,如果 j 和 k 有直接连边,且 j 能到达,k 不能到达的话,f[ i+(1<<k) ] = min( f[ i ] + deep[ i ][ j ] * a[ j ][ k ])。
其中 deep[ i ][ j ] 表示在状态为i的情况下, j 离初始点的距离。
这样基本的DP模型就出来了。
但是 deep[ i ]怎么求呢?
可以在dp的过程中做,如果 i+(1<<j) 的状态最优从 i 来,那么 deep[ i+(1<<j) ] = deep[ i ]
(除了 j 点以外,因为 j 点是新加入的。)
附代码:
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#define MAXN 15
#define MAX 999999999
using namespace std;
int n,m,S,ans=MAX;
int a[MAXN][MAXN],f[1<<MAXN],deep[MAXN][1<<MAXN];
inline int read(){
int date=0,w=1;char c=0;
while(c<'0'||c>'9'){if(c=='-')w=-1;c=getchar();}
while(c>='0'&&c<='9'){date=date*10+c-'0';c=getchar();}
return date*w;
}
int dp(int rt){
memset(deep,0,sizeof(deep));
memset(f,(MAX/1000),sizeof(f));
f[1<<rt]=0;deep[rt][1<<rt]=1;
for(int s=0;s<=S;s++)
for(int i=0;i<n;i++)
if(s&(1<<i))
for(int j=0;j<n;j++)
if(!(s&(1<<j))&&a[i][j]!=MAX&&a[i][j]!=0){
int u=(1<<j),x=f[s]+deep[i][s]*a[i][j];
if(f[s+u]>x){
f[s+u]=x;
for(int k=0;k<n;k++)deep[k][s+u]=deep[k][s];
deep[j][s+u]=deep[i][s]+1;
}
}
return f[S];
}
int main(){
int u,v,w;
n=read();m=read();
S=(1<<n)-1;
for(int i=0;i<=n;i++)
for(int j=0;j<=n;j++)
a[i][j]=(i==j)?0:MAX;
for(int i=1;i<=m;i++){
u=read()-1;v=read()-1;w=read();
if(a[u][v]>w)a[u][v]=a[v][u]=w;
}
for(int i=0;i<n;i++)ans=min(ans,dp(i));
printf("%d
",ans);
return 0;
}
这样程序的时间复杂度为O(2^n*n^4)。
这样看上去会超时。。。
但是因为状压DP会有很多可以忽略的状态的特性,时间复杂度远远没有这么高,是可以过的。
如果真的不能过呢?(其实被卡了也就80~90分,还有个10来分遇到NOIP这种情况就算了吧。。。)
没关系,我们还有一个杀手锏——随机化算法:模!拟!退!火!
先讲一个前置算法:爬山算法
爬山算法,即 Hill Climbing,简称HC。
爬山算法每次在当前找到的方案附近寻找一个新的方案(常见方式是随机一个差值),然后如果这个解更优那么直接转移。
对于单峰函数来说这显然可以直接找到最优解(不过你都知道它是单峰函数了为啥不三分呢?)
但是,假如是下面这个图呢?
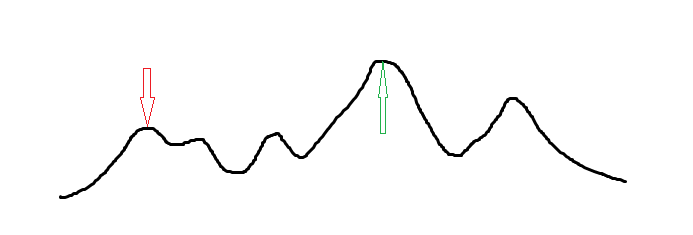
我们发现爬山算法会卡在某个“最高点”的牢笼中,无法跳出,这时候,模拟退火的优点就体现了出来。
模拟退火:
模拟退火,即 Simulated Annealing,简称SA。
模拟退火算法可以有效的解决这个陷入局部最优解的问题从而找到一个全局最优解。
实际上模拟退火算法也是贪心算法,只不过它在这个基础上增加了随机因素。
这个随机因素就是:以一定的概率来接受一个比单前解要差的解。
通过这个随机因素使得算法有可能跳出这个局部最优解。
然后你就可以不用管什么起源啦、参数啦啥的,只要知道退火过程就行了:
1、初始化:设置参数(初始温度T、终止条件T<1,衰减函数T=a*T,Mapkob链长)
2、在给定温度下,不断产生新解
3、降低温度T,回到第二步
4、结束
基本上就是这个图(来自Wikipedia):
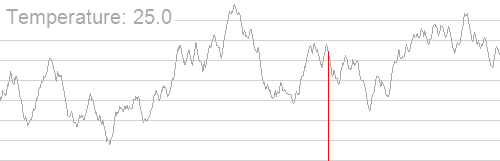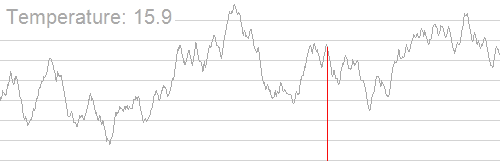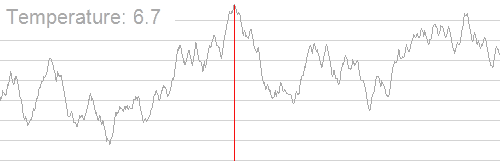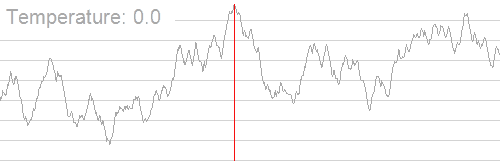
所以,上面的那题就可以随便跑了。。。
但是,这样如何保证得到全局最优解呢?有的时候得到的结果还不如贪心呢
是的,一次运行的结果并不一定最优。
但是,模拟退火的时间复杂度与贪心相同,运行几千次甚至上万次的时间都是可承受的,运行这么多次,得到最优解的几率非常大。
所以这个算法经常用于骗分。。。
附代码:
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<queue>
#define MAXN 15
#define MAXM 1010
#define MAX 2147483646
using namespace std;
int n,m;
int deep[MAXN],a[MAXN][MAXN];
bool vis[MAXN];
struct node{
int x,to;
bool operator <(const node &p)const{
return deep[x]*a[x][to]>deep[p.x]*a[p.x][p.to];
}
};
inline int read(){
int date=0,w=1;char c=0;
while(c<'0'||c>'9'){if(c=='-')w=-1;c=getchar();}
while(c>='0'&&c<='9'){date=date*10+c-'0';c=getchar();}
return date*w;
}
int solve(int rt){
int cost=0,top=0;
node u,v,past[MAXM];
memset(deep,0,sizeof(deep));
memset(vis,false,sizeof(vis));
priority_queue<node> q;
deep[rt]=1;
vis[rt]=true;
for(int i=1;i<=n;i++)
if(a[rt][i]!=MAX){
u.x=rt;u.to=i;
q.push(u);
}
for(int i=2;i<=n;i++){
u=q.top();
q.pop();
while(!q.empty()&&(vis[u.to]||rand()%n<1)){
if(!vis[u.to])past[++top]=u;
u=q.top();
q.pop();
}
vis[u.to]=true;
deep[u.to]=deep[u.x]+1;
while(top)q.push(past[top--]);
top=0;
for(int i=1;i<=n;i++)
if(a[u.to][i]!=MAX&&!vis[i]){
v.x=u.to;v.to=i;
q.push(v);
}
cost+=a[u.x][u.to]*deep[u.x];
}
return cost;
}
void work(){
int ans=MAX;
for(int cases=1;cases<=1000;cases++)
for(int i=1;i<=n;i++)
ans=min(ans,solve(i));
printf("%d
",ans);
}
void init(){
int u,v,w;
srand(2002);
n=read();m=read();
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
a[i][j]=MAX;
for(int i=1;i<=m;i++){
u=read();v=read();w=read();
a[u][v]=a[v][u]=min(w,a[u][v]);
}
}
int main(){
init();
work();
return 0;
}
最后一点:参数调整
啊,这个问题没有什么好的路子走,只有一条路——对拍!
其实随机种子是多少不是什么问题,毕竟这是一个骗分算法。。。
所以这时候就要看你的信息直(ren)觉(pin)了。。。
(据说把随机种子调成女友生日会有神秘彩蛋哦!)
后记:
附上洛谷的两次提交:
状压DP: Accepted 100
152ms / 4.08MB
代码:1.1KB C++
模拟退火:Accepted 100
280ms / 2.21MB
代码:1.61KB C++
相比之下,模拟退火的思维难度远远低于状压DP,而性能只比状压DP差一点,所以还是很强的。
如果有什么题目在考场上实在写不出来,就用模拟退火骗骗分吧!